AcWing算法基础课笔记 ------ 第二章数据结构

本篇记录一下AcWing上第二章的笔记，这一章收获也很多，学会了用数组去模拟链表，复习了一遍KMP，求表达式，以及新的一些数据结构，字典树，并查集，还有更为高效的哈希表。

文章目录

一. 单链表
二. 双链表
三. 栈
- 1. 表达式求值
- 2. 单调栈
四. 队列
- 1. 滑动窗口求最大值和最小值
五. KMP算法
六. 字典树
七. 并查集
八. 堆
九. 哈希表
- 1. 开放寻址法
- 2. 拉链法
- 3. 字符串哈希

一. 单链表

以前学习的单链表是写一个结构体出来，一个是val，另一个是指针，然后用malloc动态的开辟空间，一直newnode。
而在本讲中是利用数组来模拟实现一个单链表。
其实万变不离其宗，对于链表的增删查改操作其实都是一个意思。
就比如在链表中的头插是下面这个样子:

//AddHead
newnode = BuyNode(val);
newnode -> next = head -> next;
head -> next = newnode;//Delete 可以删除cur 所指向的下一个节点
cur -> next = cur -> next -> next;

而数组中的是：

//AddHead
data[idx] = val;	//这一步就是BuyNode
next[idx] = head;	//链接头节点的
head = idx++;		////Delete 删除cur后面的节点
next[cur] = next[next[cur]].

在本讲中是用一个题来更好的帮助理解单链表。
题目中的三个函数对应着增和删。
题目链接
下面是整体的代码:

#include <stdio.h>#define N (100000 + 10)//单链表：
//head 头节点
//idx 下一个位置的下标，也即是newNode的位置。
//data 数据
//next 下一个位置的指针
int data[N],next[N],idx,head;//初始化
void Init()
{head = -1, idx = 0;
}//头插
void AddHead(int val)
{data[idx] = val, next[idx] = head, head = idx++;
}//在k的下一个位置插入
void Insert(int k,int val)
{data[idx] = val, next[idx] = next[k], next[k] = idx++;
}//删除k的下一个节点
void Delete(int k)
{next[k] = next[next[k]];
}int main()
{int n,i;scanf("%d",&n);//Init();while(n--){int val,k;char oper;scanf(" %c",&oper);if(oper == 'H'){scanf("%d",&val);AddHead(val);}else if(oper == 'I'){scanf("%d%d",&k,&val);Insert(k - 1,val);}else{//Deletescanf("%d",&k);if(k == 0)head = next[head];Delete(k-1);}}for (i = head; i != -1; i = next[i]){printf("%d ",data[i]);}return 0;
}

二. 双链表

双链表呢就是说每个节点有两个指针和数据组成，prev指向前一个节点，next指向下一个节点。

对于双链表来说其实也和用结构体定义的那种指针方式是一样的，只要直到其增删查改的原理，换成数组也是一样的，只是表达方式不一样，额以前学习知识的时候，老师经常所说的换汤不换药就是这么个道理
要注意的是，用数组模拟链表的话，我们将0位置当head，1位置当tail
所以最开始初始化的时候可以先将0和1链接起来相当于一个空表，然后inx从2开始就好了
add操作 — 在第k个节点的下一个位置插入新节点
data[idx] = val, next[idx] = next[k],prev[idx] = k,新节点的操作
prev[next[k]] = idx,next[k] = idx; 重新链接新节点的操作。
Delet — 删除第k个节点。

因为idx从下标为2的位置开始，所以调用链表函数的时候，需要将所有的k转化成k+1.

#include <stdio.h>
#include <string.h>#define N 100000int prev[N],data[N],next[N];
int idx;void Init()
{next[0] = 1, prev[1] = 0;//此注释打开即可模拟处循环链表。//prev[0] = 1, next[1] = 0;idx = 2;
}//在第k个元素的下一个位置插入一个数
void Add(int k, int val)
{//newnode 的操作data[idx] = val;next[idx] = next[k];prev[idx] = k;//重新链接prev[next[k]] = idx;next[k] = idx;idx++;
}//删除k的下一个节点
void Delete(int k)
{next[prev[k]] = next[k];prev[next[k]] = prev[k];
}int main()
{int n,i;scanf("%d",&n);Init();while(n--){char op[5];int x,k;scanf("%s",op);if(!strcmp(op,"L")){scanf("%d",&x);Add(0,x);}else if(!strcmp(op,"R")){scanf("%d",&x);Add(prev[1],x);}else if(!strcmp(op,"D")){scanf("%d",&k);Delete(k + 1);}else if(!strcmp(op, "IL")){scanf("%d%d",&k,&x);Add(prev[k + 1],x);}else{scanf("%d%d",&k,&x);Add(k + 1, x);}}//printf("head: %d %d\n",prev[0],next[0]);//printf("tail :%d %d\n",prev[1],next[1]);for (i = next[0]; i != 1; i = next[i]) printf("%d ",data[i]);return 0;
}

三. 栈

栈和队列也都是用数组可以模拟出来，嘿，嘿，这个我熟，C语言刷题每次遇到栈，只能手写一个，不过也不费什么时间😂，这个看个人习惯吧，我是习惯于从1开始放数据，然后top = 0，就是栈空。
这个代码是我每次用栈的方式

int stk[N];
int top = 0;
//push
stk[++top];
//pop
top--;
//getTop	//获取栈顶元素
stk[top];
//isempty
top == 0 ?;

下面看看一道经典的题目把，求一个表达式的值。

1. 表达式求值

在leetcode上做过类似的题目，但是都没有这个全面，以前做过一道只有+ -的，还有只有+ -然后包含括号的等等。
这次的题目是 + - * / 然后包含括号。

首先需要两个栈，一个存放操作符号，还有一个存放数。
在遍历字符串的时候又有一下几种情况

s[i] 是数字的话，就把它的num求出来，记得更新 i 的位置
如果是（啥也不干，入栈就好了
如果是）就说明改出栈，因为不管什么优先级，都应该先算括号里面的数。
最后就是4中操作符的情况，要注意，如果新的操作符需要入栈时候，判断栈顶的操作符的优先级是否大于等于需要入栈的操作符，如果大于等于的话，那么就先对当前栈顶进行操作，然后再入栈。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>#define N (100000 + 10)int stkNums[N];
char stkOper[N];
int operTop,numsTop;void eval()
{int y = stkNums[numsTop--];int x = stkNums[numsTop--];char op = stkOper[operTop--];int ans = 0;if(op == '+') ans = x + y;else if(op == '-')  ans = x - y;else if(op == '*')  ans = x * y;else if(op == '/')  ans = x / y;stkNums[++numsTop] = ans;}int main()
{//操作符优先级int map[50];map['+'] = 1,map['-'] = 1,map['*'] = 2,map['/']= 2;//读入表达式char s[N];scanf("%s",s);int len = strlen(s);int i;//遍历表达式for (i = 0; i < len; i++){if(isdigit(s[i])){//入数字栈int num = 0;int j = i;while(j < len && isdigit(s[j])){num = num * 10 + s[j++] - '0';}         i = j - 1;stkNums[++numsTop] = num;}else if(s[i] == '('){stkOper[++operTop] = s[i];}else if(s[i] == ')'){while(stkOper[operTop] != '('){eval();}operTop--;}else{while(operTop != 0 && map[stkOper[operTop]] >= map[s[i]]){eval();}stkOper[++operTop] = s[i];}}while(operTop != 0){eval();}printf("%d\n",stkNums[numsTop]);return 0;
}

2. 单调栈

单调栈就是是一个栈呈单调递增或者递减的形式维护，然后利用整个栈就得到想要的结果，题目关于求 " 下一个更大的……" 这类题目。
下面是一道求解左边第一个更小的数据，没有的话打印-1.

我们用一个单调递增的栈维护。
这样子在入栈的时候栈顶的元素就是左边第一个比子小的元素。
如果栈为空，就说明自己最小，使其出栈出完了，或者说是自己处于边界，这类情况打印-1就好了。

#include <stdio.h>#define N 100010int stk[N],top;int main()
{int i,n,x;scanf("%d",&n);for (i = 0; i < n; i++){scanf("%d",&x);while(top != 0 && stk[top] >= x){top--;}if(top == 0)printf("-1 ");elseprintf("%d ",stk[top]);stk[++top] = x;}return 0;
}

四. 队列

队列也可以用数组来模拟，前些天还在刷单调队列的，当然每个人模拟队列的方式是不同的，看自己习惯吧。
下面是我用数组模拟的队列的方式：

int que[N];
int front = 0, rear = 0;//push
que[rear++];//pop
que[front++];//不仅能获取队首，还能获取队尾
que[front]; 	//队首
que[rear - 1];	//队尾//isempty
front == rear ?

那队列中也有一种叫单调队列的东西，还有一种叫做优先队列但是也可以叫做堆，堆又跟树有关系了，在这里就先不说优先队列（堆）了，先看单调队列吧。

单调队列和单调栈是一样的，都是维护其单调递增减，只是push和pop的操作方式不一致

而单调队列应用最多的就是在滑动窗口这种算法中。

1. 滑动窗口求最大值和最小值

该题也是AcWing上面的题目，链接在这里。
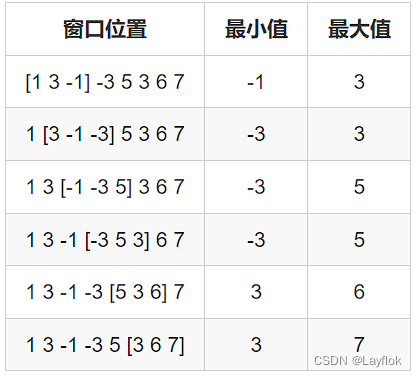
在这里插入图片描述
这道题我之前也做过，在之前的文章中也有，所以这里就不太细的展开叙述了，总体思路是一样的，只是人家的更简洁。
链接

我之前的代码中是利用两个指针left 和 right 来指向窗口的边界，然后每次更新窗口的时候获取当前窗口的答案
而下面的代码中则是只要i > k - 1,就获取结果，更新窗口边界的条件变成了
i - k + 1 > que[front] 于我之前的 right - left + 1 > k 不同。

#include <stdio.h>#define N 1000010int que[N], front, rear;
int nums[N];int main()
{int i, j, n, k;scanf("%d%d",&n,&k);for (i = 0; i < n; i++) scanf("%d",&nums[i]);//最小值for (i = 0; i < n; i++){if(front != rear && i - k + 1 > que[front]) front++;while(front != rear && nums[que[rear - 1]] >= nums[i]) rear--;que[rear++] = i;if(i >= k - 1){printf("%d ",nums[que[front]]);}}printf("\n");//最小值front = 0, rear = 0;for (i = 0; i < n; i++){if(front != rear && i - k + 1 > que[front]) front++;while(front != rear && nums[que[rear - 1]] <= nums[i]) rear--;que[rear++] = i;if(i >= k - 1){printf("%d ",nums[que[front]]);}}printf("\n");return 0;
}

五. KMP算法

kmp算法从学到至今，每每想起来都是痛苦的，很难，但是本讲中，y总讲的还是非常的清楚了，感觉比之前自己琢磨的有深入了一点，知识嘛，总是后面的每一遍都会比其前面有着不一样的收获。
子串和主串的下标都是从1开始。

咱先抛开next数组不说，就单纯的说一下kmp匹配的思想是什么。
利用两个指针，i和j分别指向主串str 与子串 subStr, 注意 j 可以取成0或者是1.
那么相应的往回倒退的时候，就需要j = next [j] || j = next[j - 1]两种中的其一。
我在此采取 j = 0，然后利用 j = next [j] 的方式进行回退.
然后取遍历子串和主串，如果在当前位置上遇到的字符不同，那么j需要采取倒退的方式去，直到遇到相同的字符，或者说 j = 0，退到起点的位置，就不需要去倒退了。
否则的话就是str[i] == str[ j + 1] ，然后 j ++ 指向下一个就好了
但要注意的是如果 j == 子串大小，就说明找完了，匹配成功就可以进行相应的操作。
比如说返回其起始位置，还有返回 true || false 表示是否存在此子串等等，看具体的应用场景即可。
代码如下：

//m 代表主串长度，n代表子串长度 ， str 和 substr都从1开始存储
for (i = 1, j = 0; i <= m; i++)
{while (j != 0 && str[i] != subStr[j + 1]){//回退j = next[j];}if (str[i] == subStr[j + 1]){j++;}if(j == n){//匹配成功，具体操作看应用场景。//如果看看有多少个子串，回退一下即可//j = next[j];}
}

那么next数组又该如何求呢，其实就像是对子串，进行一次类似于kmp匹配的操作。
注意是对子串求解next数组.

就好像是是把子串想象成主串，然后主串和子串都是一个，对其进行上述的KMP操作
— 个人总结，仅供参考

但是要注意，从下标为2 位置直接开始就好了，1的位置肯定是0嘛。它再退也不能退出去对不。
最后录入next数组的话就是 next [i] = j

//这里的范围是n 而不是m，因为是对子串进行遍历
for (i = 2, j = 0; i <= n; i++)
{while (j != 0 && subStr[i] != subStr[j + 1]){j = next[j];}if (subStr[i] == subStr[j + 1]){j++;}//next[i] = j;
}

仔细看上述的两种代码几乎是一致的。
下面是对于本题的全部代码，要求返回主串中所有该子串的起点:

#include <stdio.h>#define M 1000010 //主串大小
#define N 100010  //子串char str[M],subStr[N];
int next[N];int main()
{int n,m;scanf("%d%s%d%s",&n,subStr + 1,&m,str + 1);int i,j;//next数组for (i = 2, j = 0; i <= n; i++){while(j != 0 && subStr[i] != subStr[j + 1]) j = next[j];if(subStr[i] == subStr[j + 1])  j++;next[i] = j;}//kmpfor (i = 1, j = 0; i <= m; i++){while(j != 0 && str[i] != subStr[j + 1])    j = next[j];if(str[i] == subStr[j + 1]) j++;if(j == n){printf("%d ", i - n);j = next[j];}}return 0;
}

六. 字典树

wc，这个牛，这个真可以，在之前我刷leetcode当是刷的是字符串，然后需要用到哈希表，反正就是需要记录每个字符串出现的次数，当时可是费了九牛二虎之力自己写了一个数据结构，像下面这个样子的，这个就是哈希表中的拉链法。
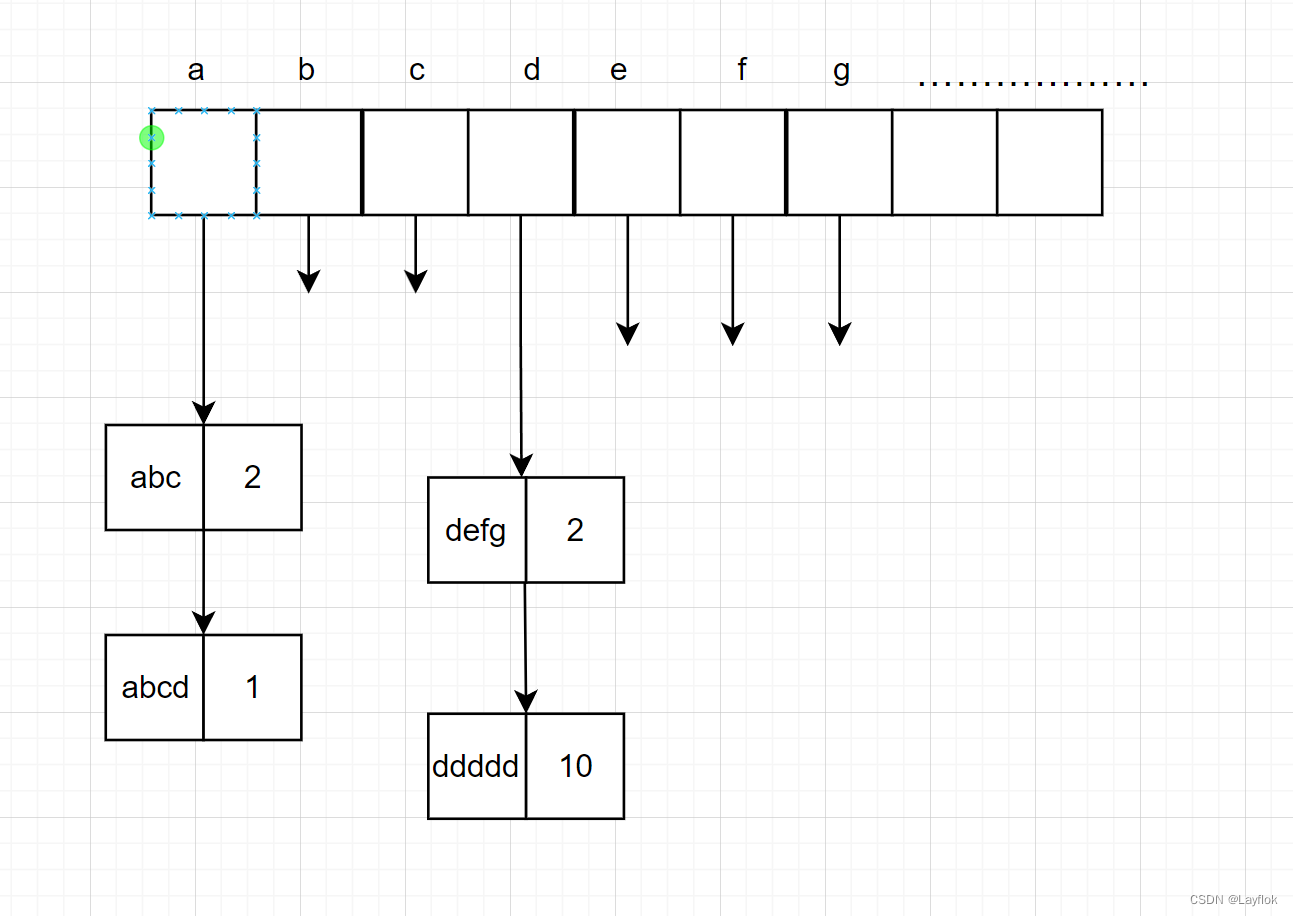
在这里插入图片描述
额。。没错，就是这个样子，开辟一个大小为26的结构体数组，每个结构体里面是放着字符串和该字符串出现的次数。
但是但是但是，从今以后，学了字典树这个东西，真香。
下面是字典树的图，画的可能有点丑陋，但是就是这个样子。
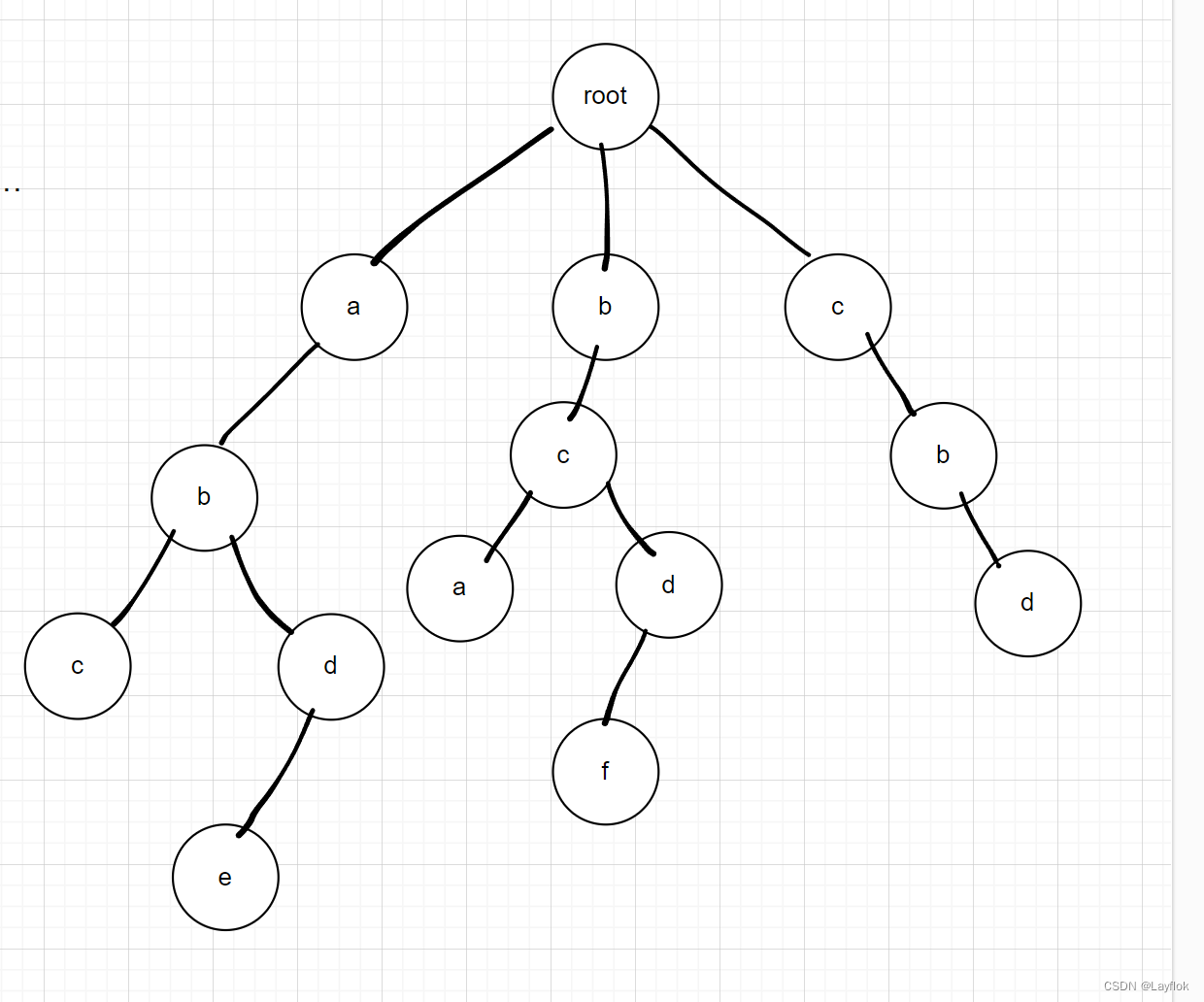
在这里插入图片描述

对其进行插入操作的话是，对插入的字符串进行遍历，然后取出每一个字母，看看字典树中是否存在，要是存在，就接着往下走，要是不存在的话，就创建一个新的节点出来，继续迭代下去，直到字符串为空。
而查找操作也是一样的，就是去查找每一个字符，如果有就迭代往下走，如果没有的话，直接返回0就好了。
删除操作也是一样的。

下面使用数组来模拟实现的，会发现三个函数的框架几乎是一致的。

#include <stdio.h>#define N 20int son[N][26],cnt[N], idx;void TrieAdd(char* s)
{int r = 0; // root  根节点int i;for (i = 0; s[i]; i++){int u = s[i] - 'a';if(son[r][u] == 0){//字母不存在，需要进行插入son[r][u] = ++idx;}//迭代下去r = son[r][u];}cnt[r]++;
}int TrieFind(char *s)
{int r = 0;int i;for (i = 0; s[i]; i++){int u = s[i] - 'a';if(son[r][u] == 0){return 0;}r = son[r][u];}return cnt[r];
}void TrieDelete(char* s)
{int r = 0;int i;for (i = 0; s[i]; i++){int u = s[i] - 'a';if(son[r][u] == 0){//无此节点 return;}r = son[r][u]; }if(cnt[r] != 0){cnt[r]--;}
}int main()
{int n;scanf("%d",&n);while(n--){char op,s[N];scanf(" %c%s",&op,s);if(op == 'I'){TrieAdd(s);}else if (op == 'D') {TrieDelete(s);}else{printf("%d\n",TrieFind(s));}}return 0;
}

七. 并查集

ok，又是一个新的名词出现了哈，那么并查集是用于处理集合与集合之间的操作。
比如：查看元素a是否在集合 X 中,或者是合并两个集合这个两个操作。

Find 函数：
Find 函数适用于查找自身的父亲节点，我们使用给一个数组p来表示当前i的父亲节点，p[i] 就是i的父亲节点。
然后我们由上公式的话就可以就可以推出一个找根节点的公式,默认根节点的父亲是自己本身。
即： while(p[x] != x) x = p[x] 这样子就可以找到自己的根节点。
但是我们反复的查找x的根节点也不行，那样时间复杂度永远都是树的高度，所以我们可以加入路径压缩，便可以在遍历一次后，使这条路上的所有节点父亲都是根节点。如下图所示：

不难看出是一个递归的操作，代码如下：

int find(int x)
{if (p[x] != x){p[x] = find(p[x])}return p[x];
}//合并操作就是将自己的父亲节点连接到另一个集合的根节点上就好了。
p[find(x)] = find(y);

接下来运用到一道题目中去，刚学完并查集我就想起来之前leetcode上做过的一道题目
给定一个图，然后再给两个点，看看是否能从sorce 到 dest去。
leetcode.1971寻找图中是否存在路径
这道题当时是用c语言建了一个图，然后对图从sorce 进行bfs算法遍历，看看dest是否访问过了。
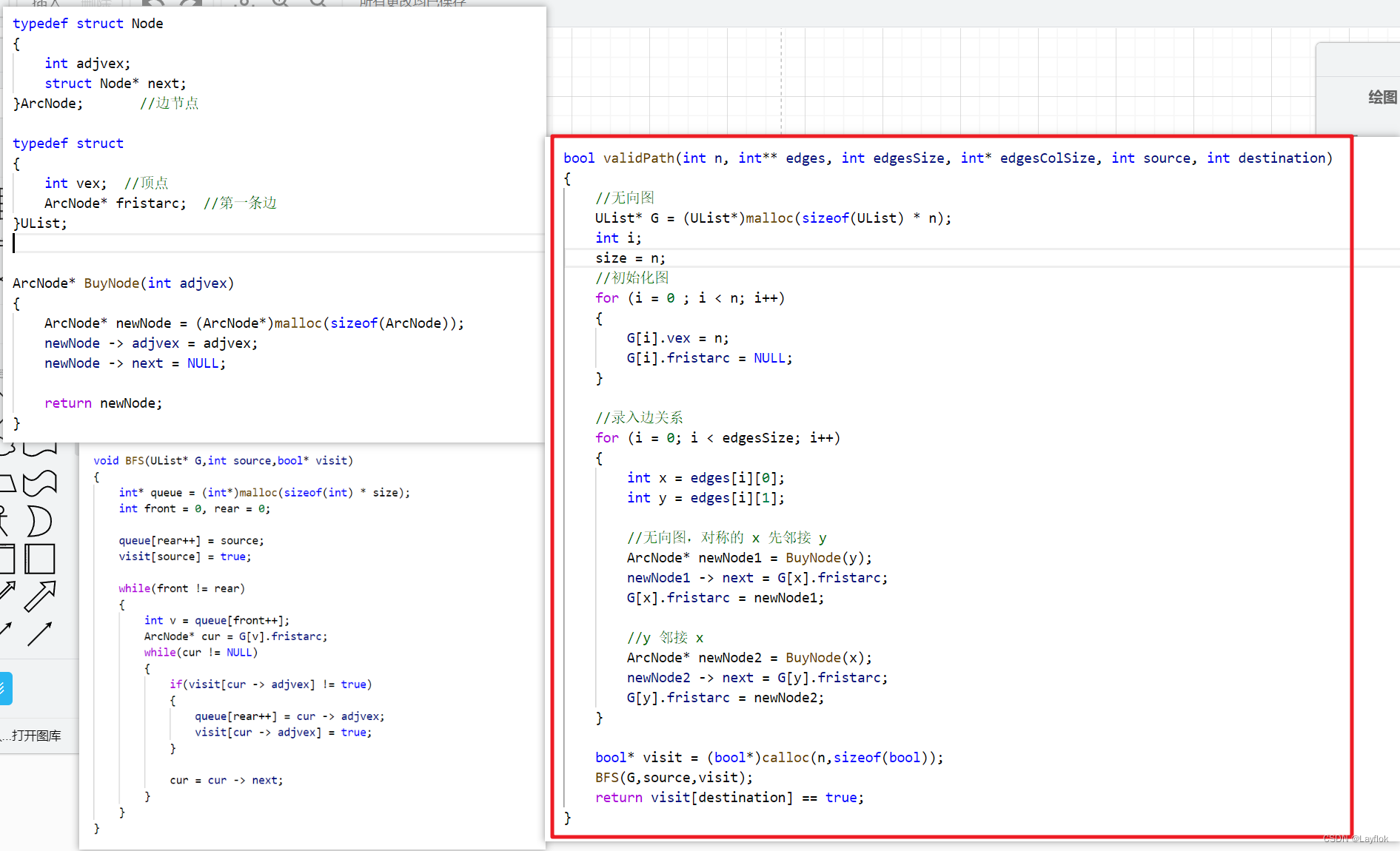
在这里插入图片描述
现在看来，用并查集直接过啊。。。。

#define N (2 * 100010)
int p[N],n;
int Find(int x)
{if(p[x] != x)p[x] = Find(p[x]);return p[x];
}
bool validPath(int n, int** edges, int edgesSize, int* edgesColSize, int source, int destination)
{int i;//初始化p数组for (i = 0; i < n; i++) p[i] = i;//创建集合for (i = 0; i < edgesSize; i++){int a = edges[i][0], b = edges[i][1];//和并集合p[Find(a)] = Find(b);}return Find(source) == Find(destination);
}

八. 堆

堆的话就是优先队列，分为小根堆和大根堆两种，根节点的值都是最小值就是小根堆，就是一种完全二叉树的结构，但是呢完全二叉树是可以用数组来存储的，之前我一直都是在0号位置存储根节点，现在看来，其实存在1号位置也不错，入乡随俗吧。
对于堆的函数，常用的有其实就那一个函数维护堆。
下面是小根堆的实现:
左孩子lc = 2 * i , 右孩子 rc = 2 * i + 1, 父亲节点 parent = i / 2.

int heap[N],size;	//根节点在1的位置存放。
//传过来的是下标
//向下调整
void Down(int i)
{int min = i,lc = 2 * i, rc = 2 * i + 1;if(lc <= size && heap[lc] < heap[min])min = lc;if(rc <= size && heap[rc] < heap[min])min = rc;if(i != min){Swap(i,min);Down(min);}
}//向上调整
void Up(int i)
{	//看看父亲节点是否大于我自身的节点while( i / 2 != 0 && heap[i / 2] > heap[i]){Swap(i / 2, i);i /= 2;}
}//建堆
for (i = size / 2; i != 0; i--)Down(i);//insert
void Add(int val)
{heap[++size] = val;Up(i);
}//删除堆顶元素
void Del(int i)
{Swap(1,size--);Down(1);
}

九. 哈希表

哈希表这个其实在平时的刷题过程中用的还是非常频繁的，我之前呢如果就是数据范围多大，我就开多大的，然后直接用数组扔进去就好，如果有负数那我就拿一个二维数组来充当哈希表。
比如数字 - 53 和 53,就会是 hash[53][0] 代表 -53，hash[53][1]代表+53
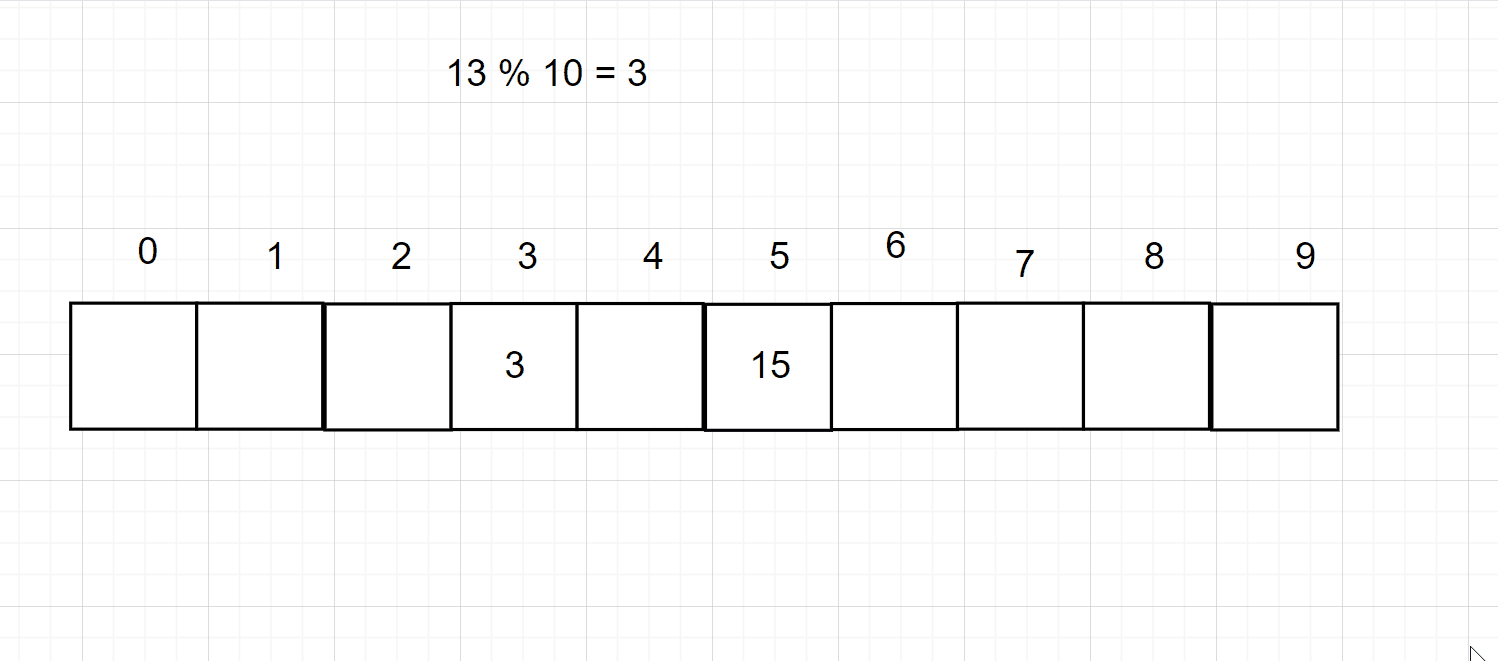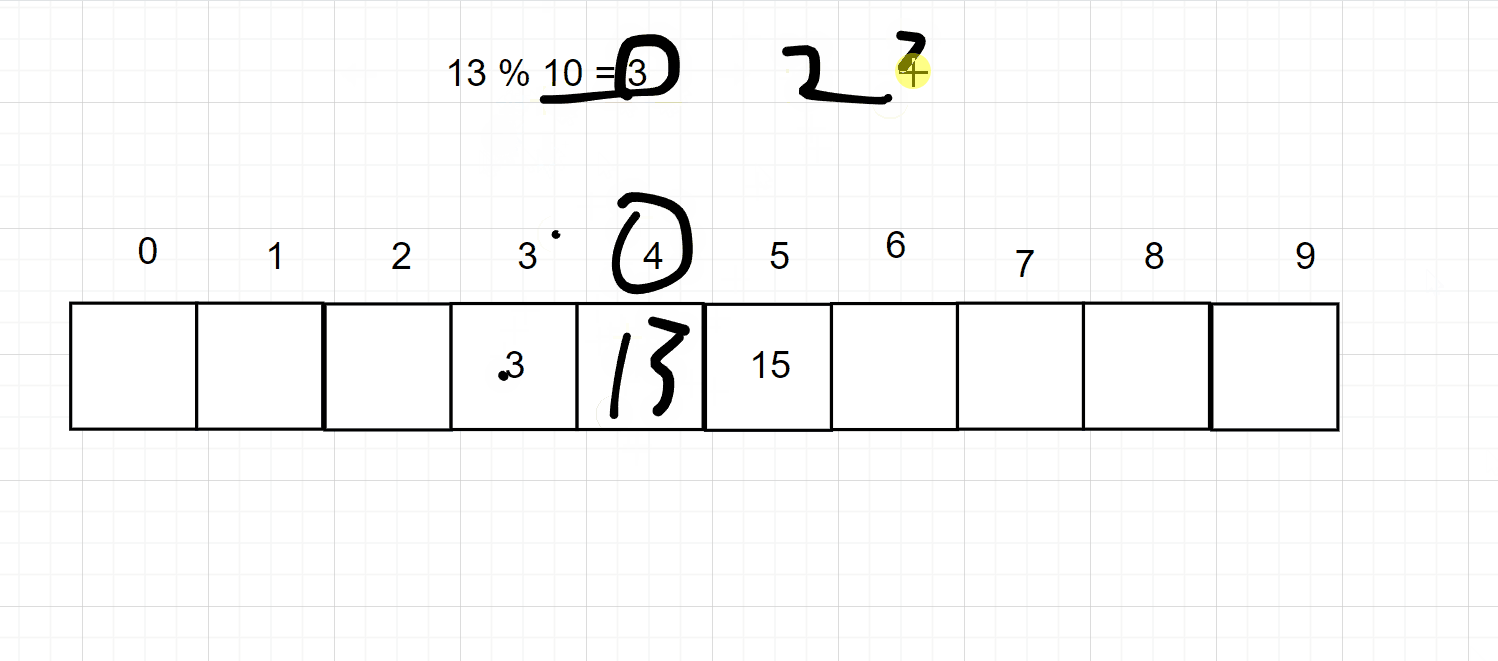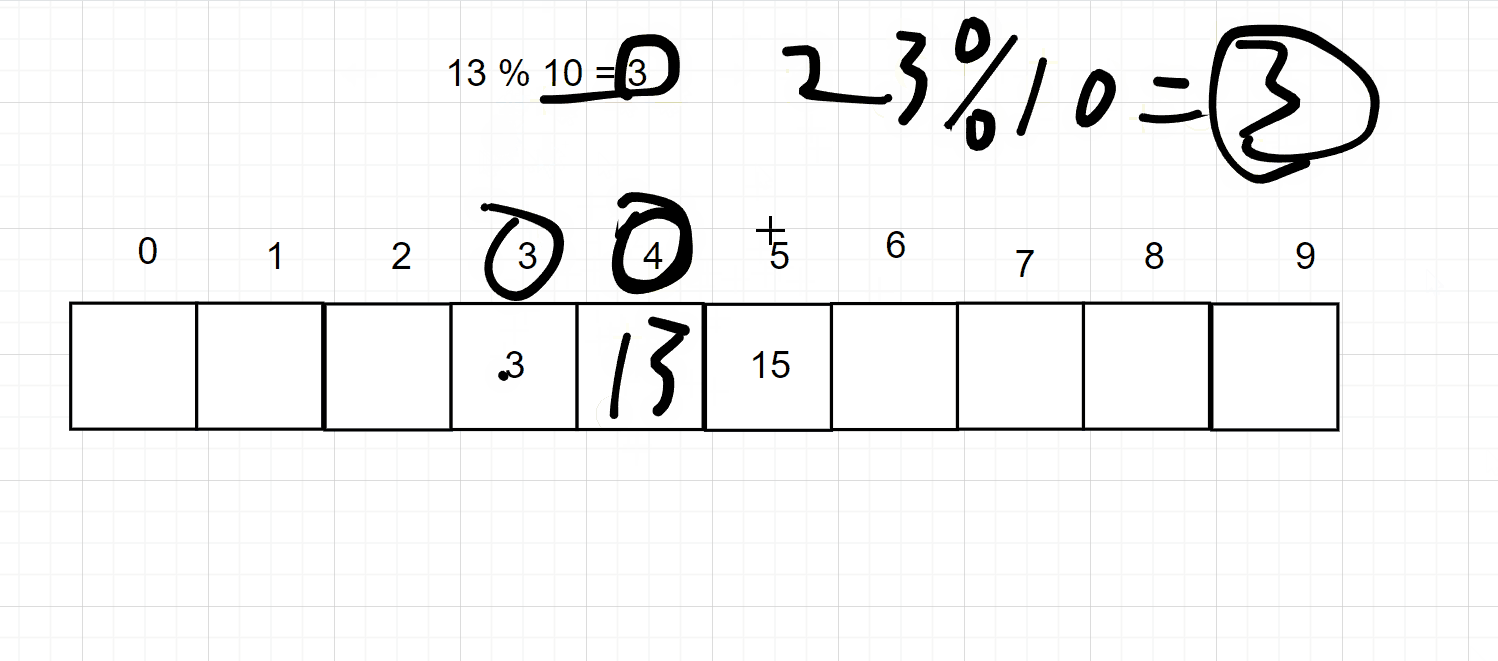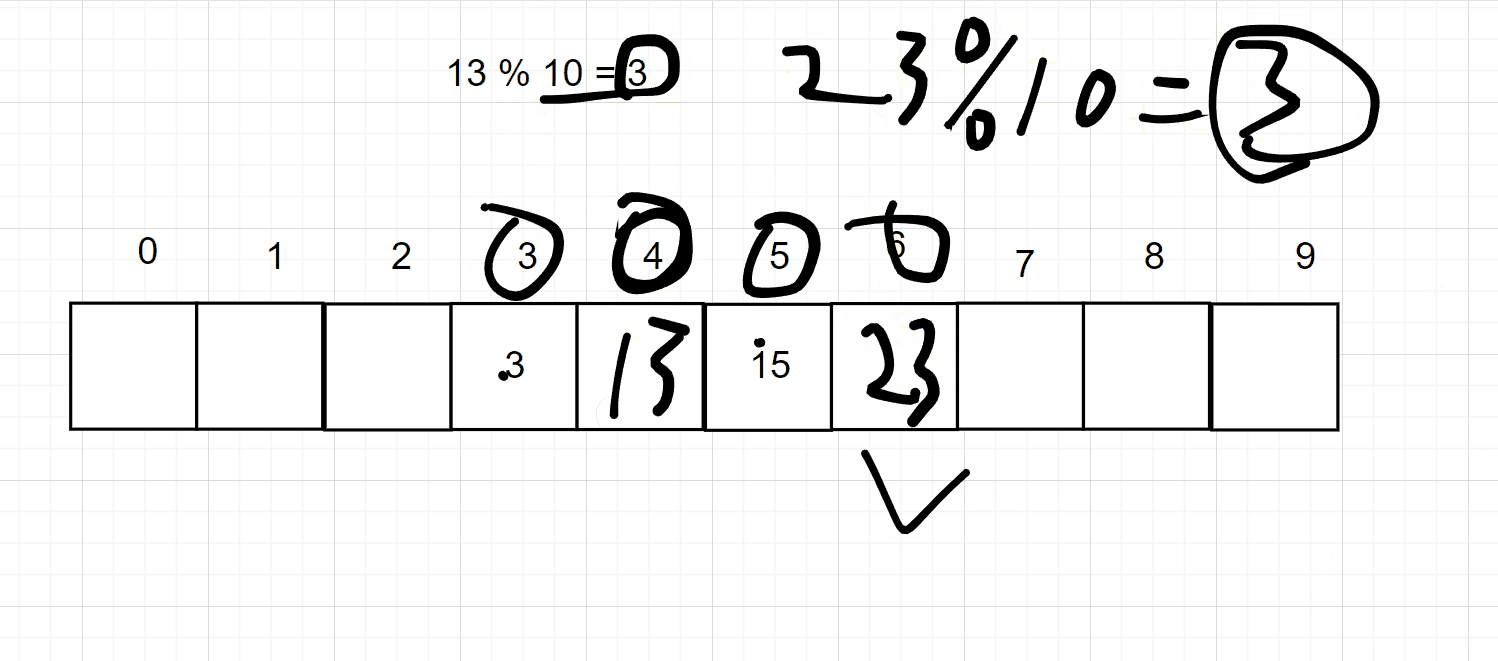
但是这个样子太浪费空间，所以可以采用一下对数据进行一个取模的操作，即可缩小你的数据大小，但是呢又会出现一个冲突的问题，比如3 % 10 = 3，存储在3的位置上
但是 13 % 10 也是3，那么3的位置上已经有值了，所以会用一下的两种方式来处理冲突。注意取模的数一般是大于哈希大小的第一个质数

1. 开放寻址法

开放地址法的意思就是说，如果当前的位置上已经存储了数据，那么就向下一个位置取，如果还有，就再向下一个位置去找，直到找到此位置为空的地方，如下图所示：
在这里插入图片描述

就是说我实现一个find函数，它的作用呢就是找到传过来的x在什么位置，
如果哈希表中没有 x 那么就正好返回了它也应该插入的位置.
但是要注意哈希表的范围需要比 拉链法大两到三倍。
代码如下：

#define N 200003int hash[N];
int NIL = 0x3f3f3f3f;int Find(int x)
{int key = (x % N + N) % N;while(hash[key] != NIL && hash[key] != x){key++;if(key == N)    //找到末尾了再返回去key = 0;}return key;
}

2. 拉链法

拉链法的我其实也是我常用的方法，然后上面的字典树中提到过，以前的字符串哈希就是用拉链法存储的，如下图所示：
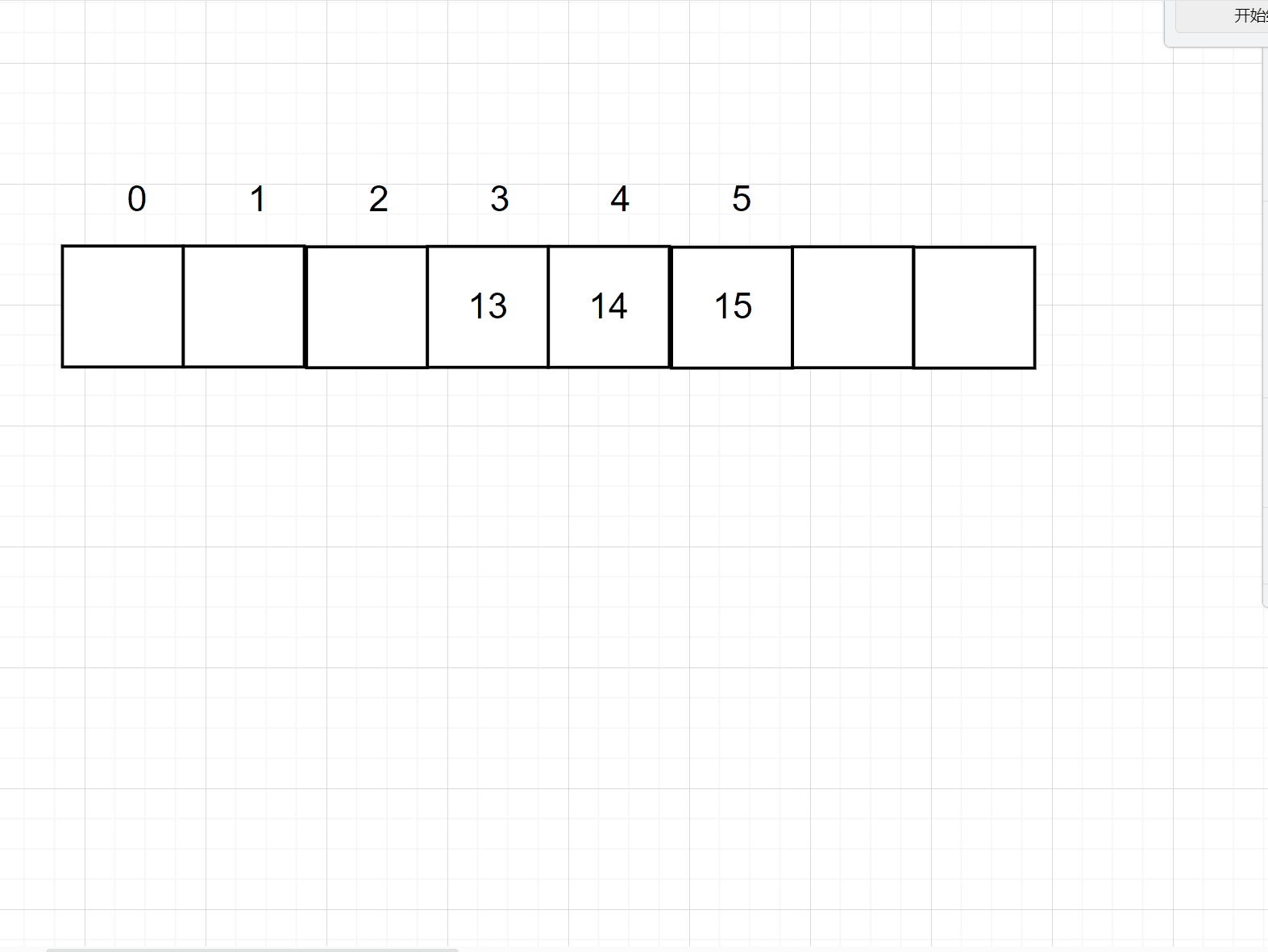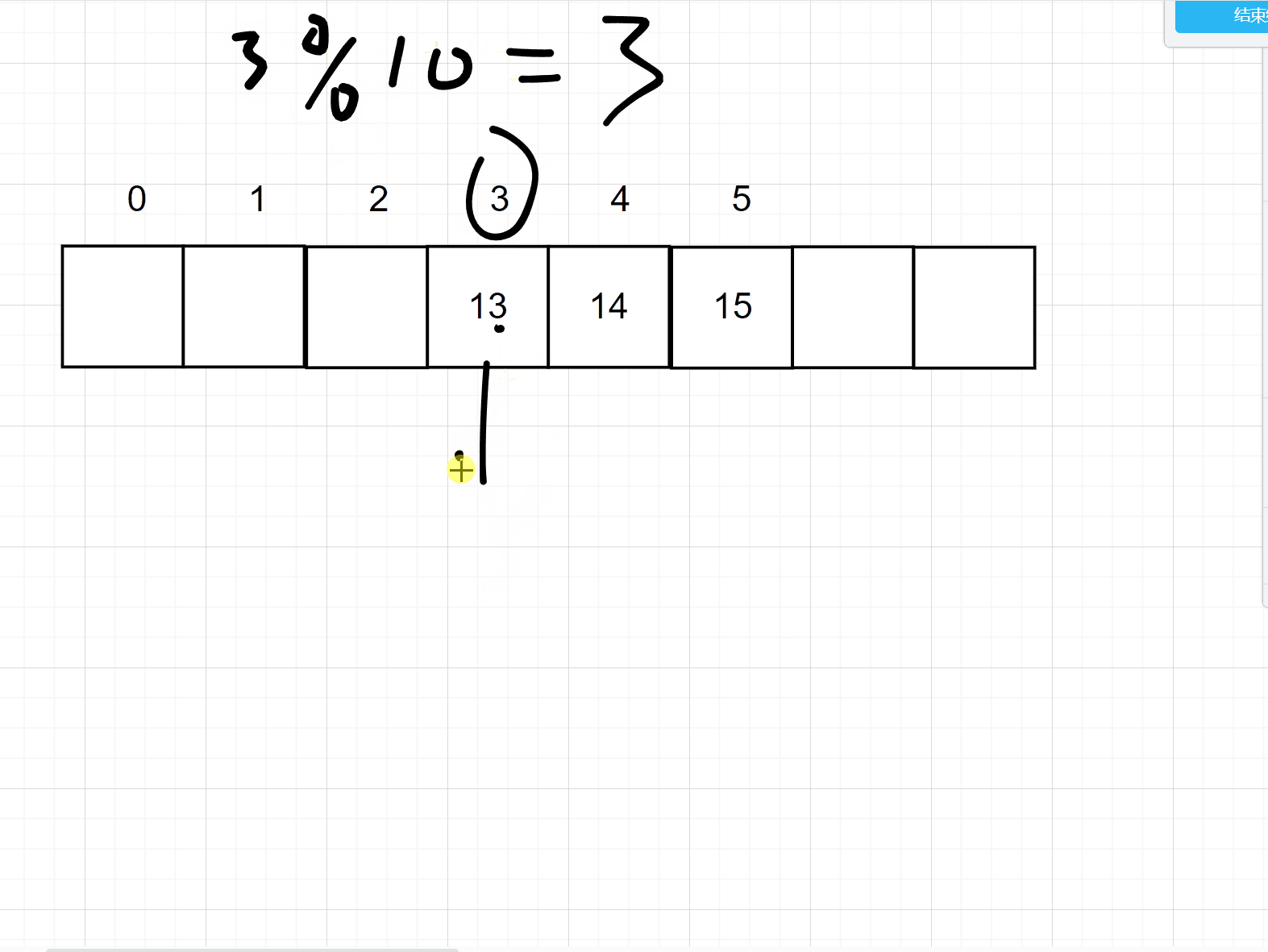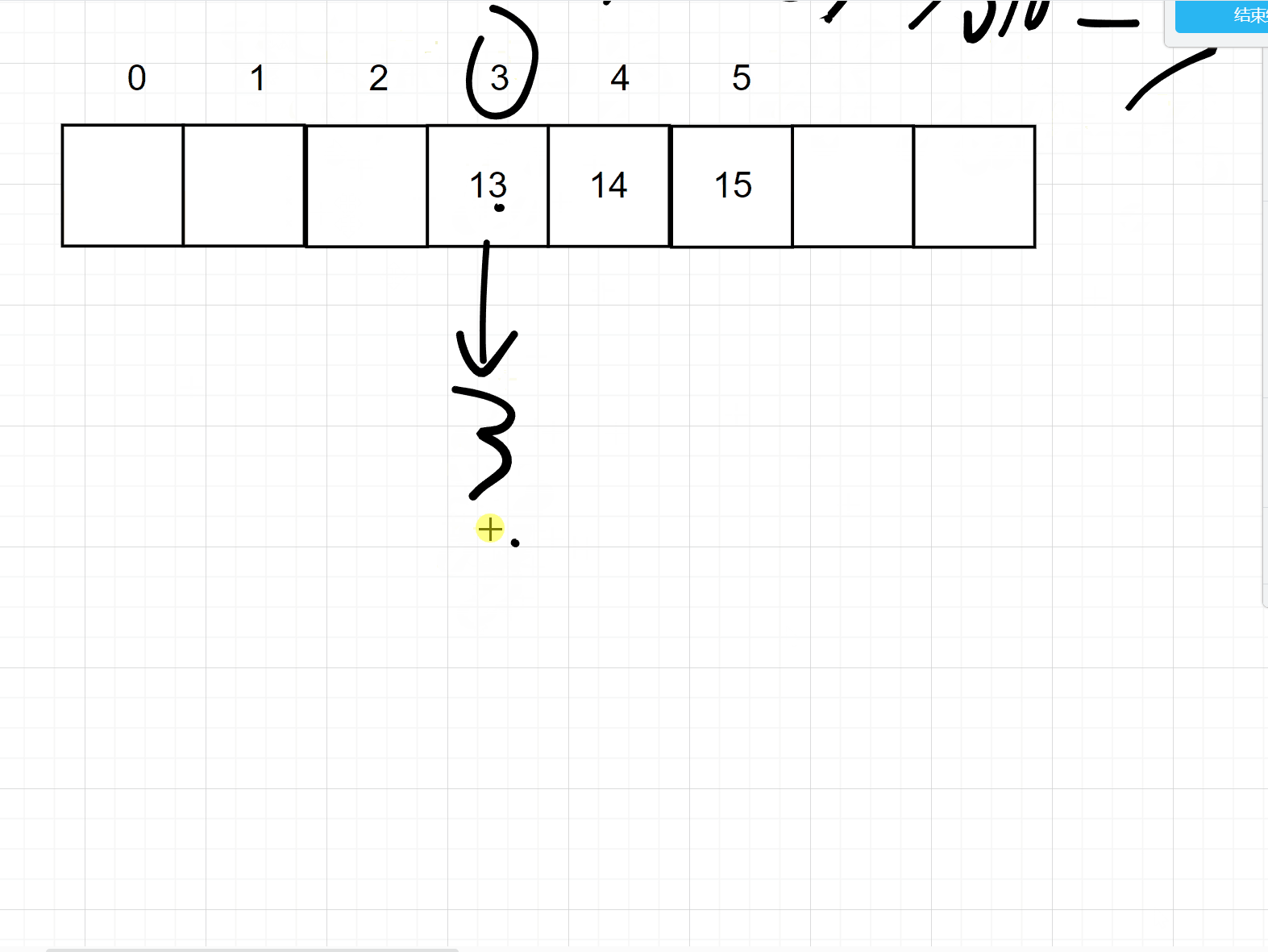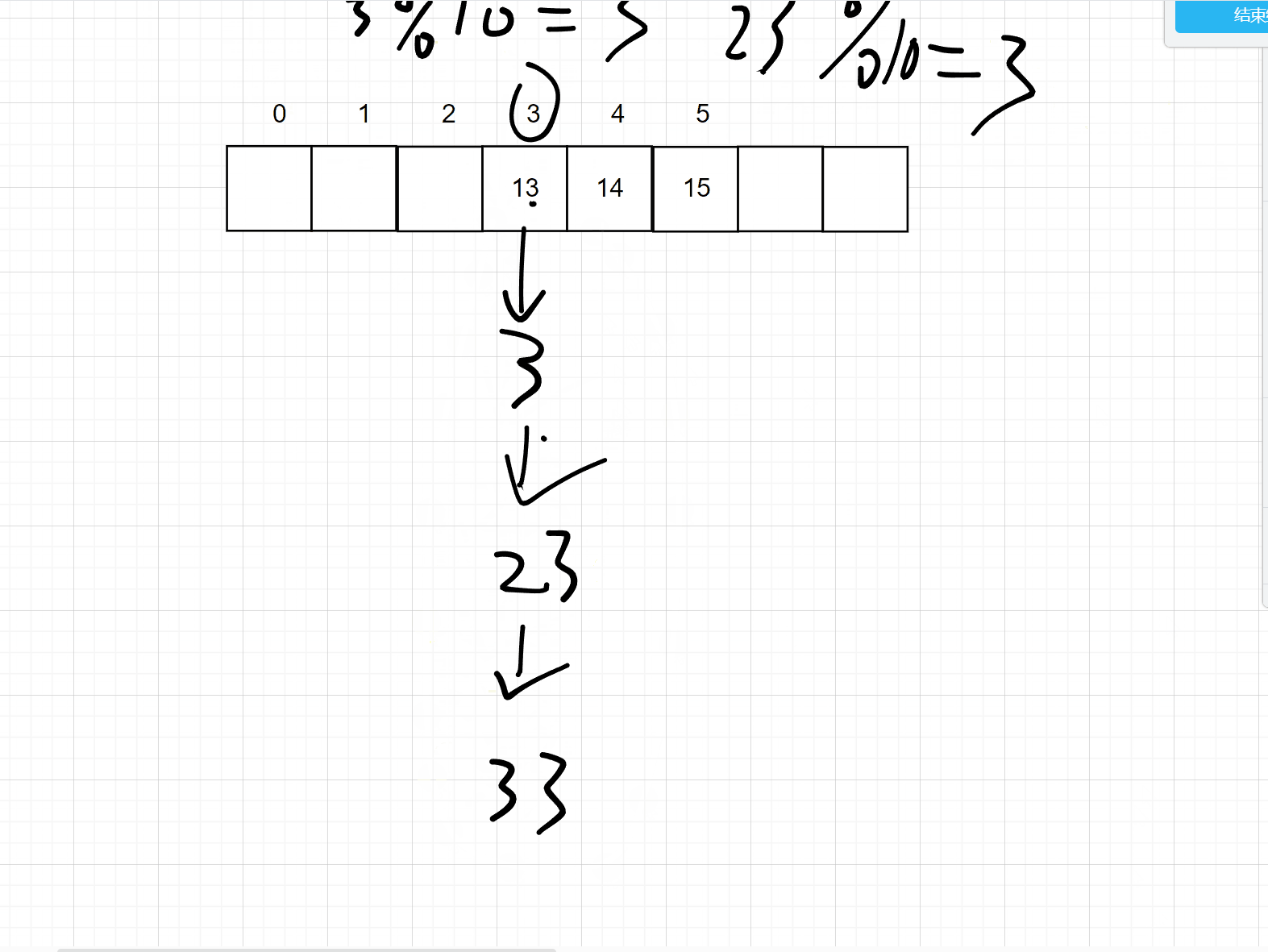
在这里插入图片描述

拉链法的话就是发现冲突的时候，直接在当前位置的下面接着用链表进行插入。
那么还需要手写一个链表？其实不用，最开始，第一部分里面有用数组模拟链表。
而对于链表上图中是用了尾插的方式是为了好画，而实际在代码中则是用头插更加方便。
这种方法呢就是不能直接找到合适的位置了，需要用到两个函数。
可以发现哈希表的大小是比开放寻址法小，但是却多开了两个数组来充当链表。
注意初始化哈希表全为 -1.

代码如下：

#define N 100003int data[N],next[N],idx;
int hash[N];void Insert(int x)
{int k = (x % N + N) % N;//单链表头插data[idx] = x,next[idx] = hash[k], hash[k] = idx++;
}bool Find(int x)
{int k = (x % N + N) % N;int i;for (i = hash[k]; i != -1; i = next[i]){if(data[i] == x)return true;}return false;
}

3. 字符串哈希

字符串哈希的话，在本讲中处理的问题就是说给定一个字符串，然后输出依次输入两对区间，看看这两对区间内的字符串是否相同。
而字符串哈希的结构就是原字符串的下标充当key表示从开始到 i 的位置的字符串，然后哈希值呢就是将这个字符串转化成一个很大的数字，用它来充当我们原来的字符串。
而对于字符串是如何转化成一个很大的数的。
下面出现的base = 131 或者 13331，至于为什么经验值会是这个，感兴趣的自己了解吧，这里就不探索了。

首先将字母 a ~ z 隐射成从 1 ~ 26，然后将其想象成一个 base = 131 的进制。
然后我们对每个字符串进行转化：
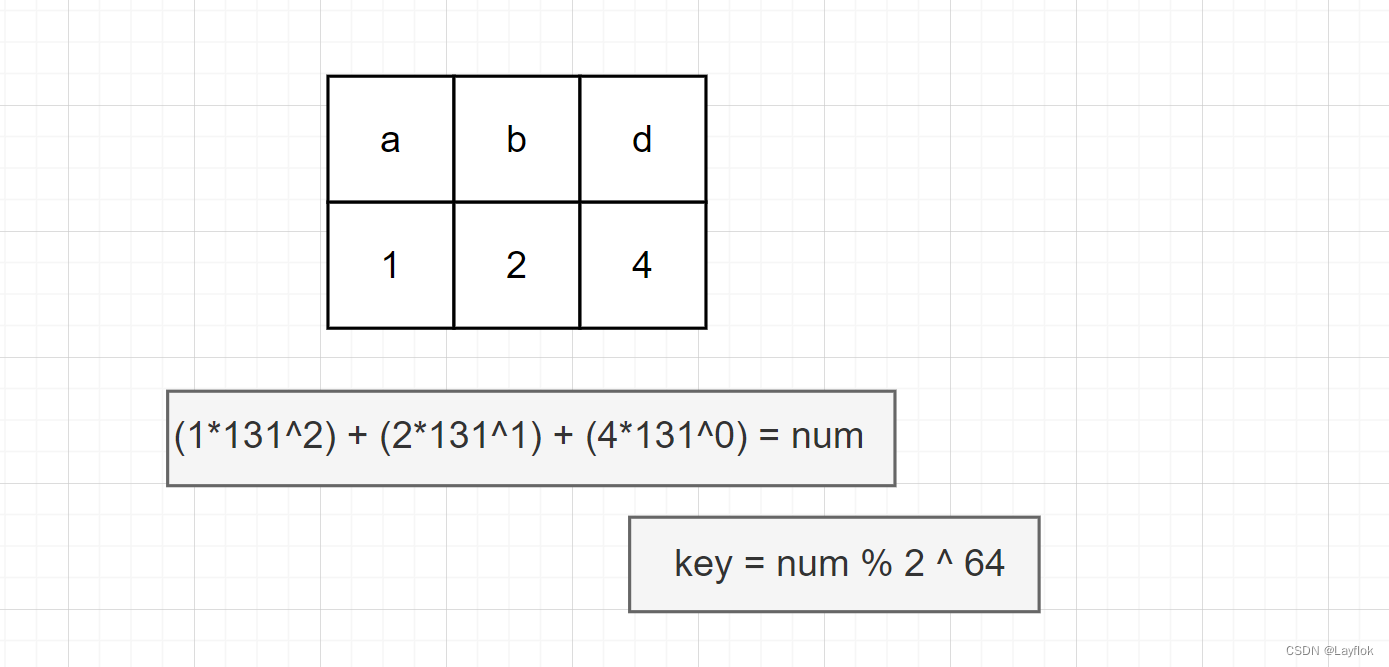
上图中对字符串转化成数字后进行取模是像前面的哈希表一样的道理，但是在实际代码过程中 unsigned long long 就是 2⁶⁴的大小，所以直接取成它的话会溢出，那么溢出后其实就是自动取模了，所以就不用管了。
那么有了这样的字符串转化成数字的公式，我们就可以利用前缀和道理，求出字符串中前 i 个字符串的哈希值是多少。
这样子我们就能求出区间[l,r]哈希值。
公式hash[r] - hash[l - 1] * p[r -l + 1] p 数组中存放的是131 的各个次方。

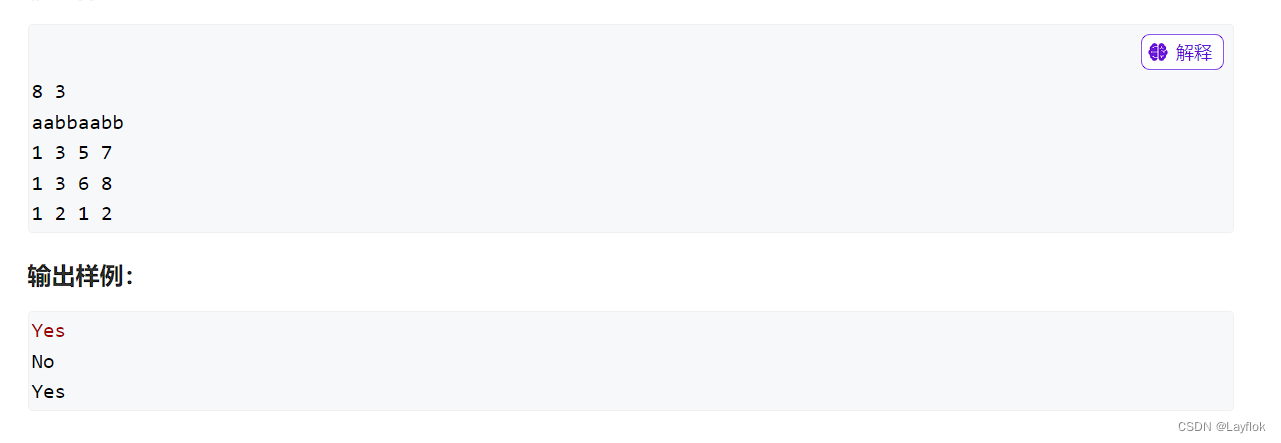
在这里插入图片描述

整体的代码如下：

#include <stdio.h>
#include <string.h>
#define N 100010typedef unsigned long long ULL;int base = 131;
ULL hash[N],p[N];   //哈希表以及base的次方
int n;
char str[N];ULL get(int l,int r)
{return hash[r] - hash[l - 1] * p[r - l + 1];
}int main()
{int m,i;scanf("%d%d%s",&n,&m,str + 1);p[0] = 1;for (i = 1; i <= n; i++){hash[i] = hash[i - 1] * base + str[i] - 'a' + 1;p[i] = p[i - 1] * base;}while(m--){int l1,r1,l2,r2;scanf("%d%d%d%d",&l1,&r1,&l2,&r2);if(get(l1,r1) == get(l2,r2))puts("Yes");elseputs("No");}return 0;
}