1.【模板】ST 表
2.Balanced Lineup G
3.景区导游
4.最近公共祖先(LCA)
倍增思想:主要用于LCA问题,RMQ问题。在进行 递推 时,如果 状态空间很大,通常的 线性递推 无法满足 时间 与 空间复杂度 的要求,那么我们可以通过 成倍增长 的方式,只递推 状态空间 中在 2 的整数次幂位置上的值 作为代表。
ST 表https://www.luogu.com.cn/problem/P3865
题目描述
给定一个长度为 �N 的数列,和 �M 次询问,求出每一次询问的区间内数字的最大值。
输入格式
第一行包含两个整数 �,�N,M,分别表示数列的长度和询问的个数。
第二行包含 �N 个整数(记为 ��ai),依次表示数列的第 �i 项。
接下来 �M 行,每行包含两个整数 ��,��li,ri,表示查询的区间为 [��,��][li,ri]。
输出格式
输出包含 �M 行,每行一个整数,依次表示每一次询问的结果。
输入输出样例
输入 #1复制
8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8输出 #1复制
9
9
7
7
9
8
7
9说明/提示
对于 30%30% 的数据,满足 1≤�,�≤101≤N,M≤10。
对于 70%70% 的数据,满足 1≤�,�≤1051≤N,M≤105。
对于 100%100% 的数据,满足 1≤�≤1051≤N≤105,1≤�≤2×1061≤M≤2×106,��∈[0,109]ai∈[0,109],1≤��≤��≤�1≤li≤ri≤N。
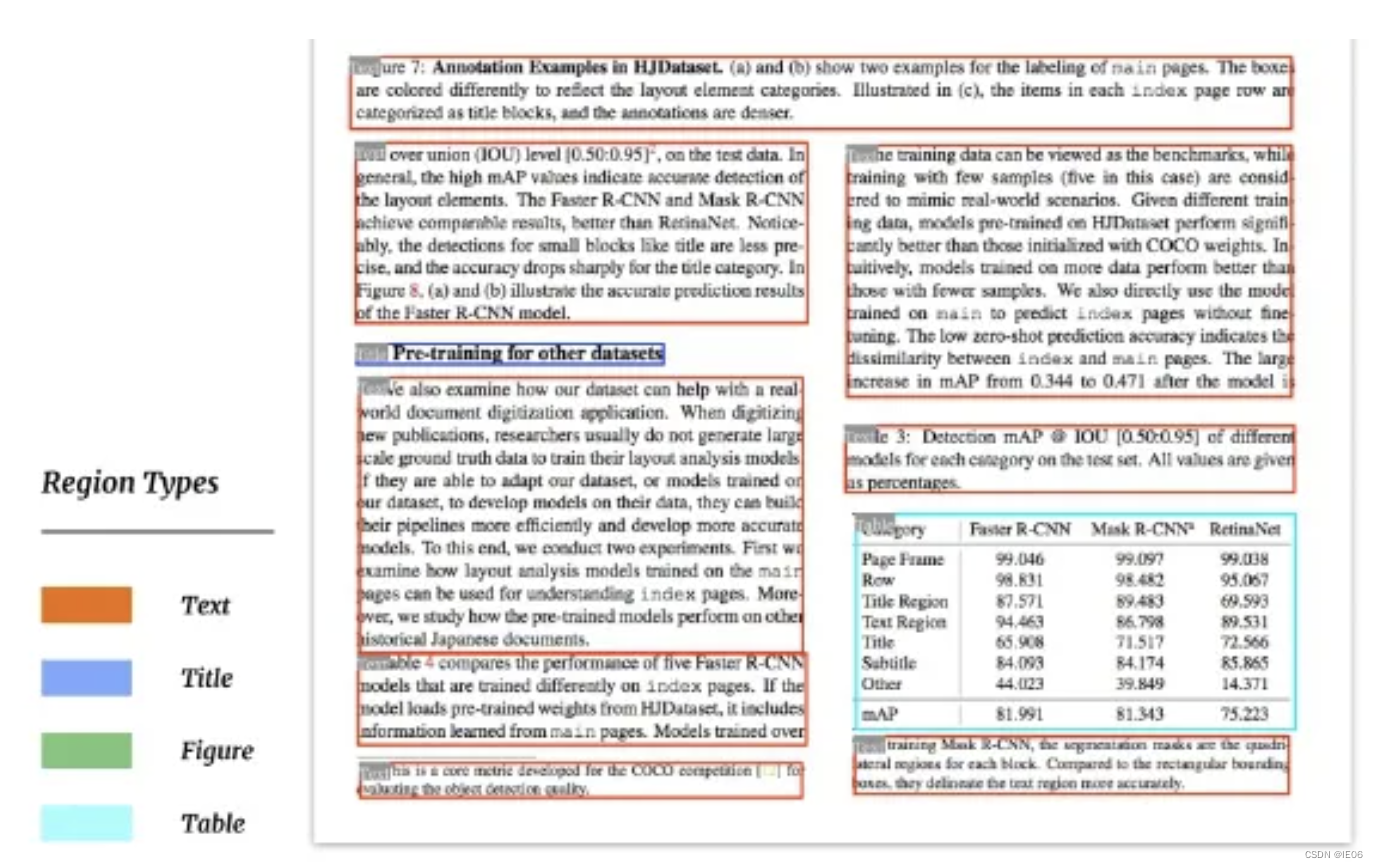
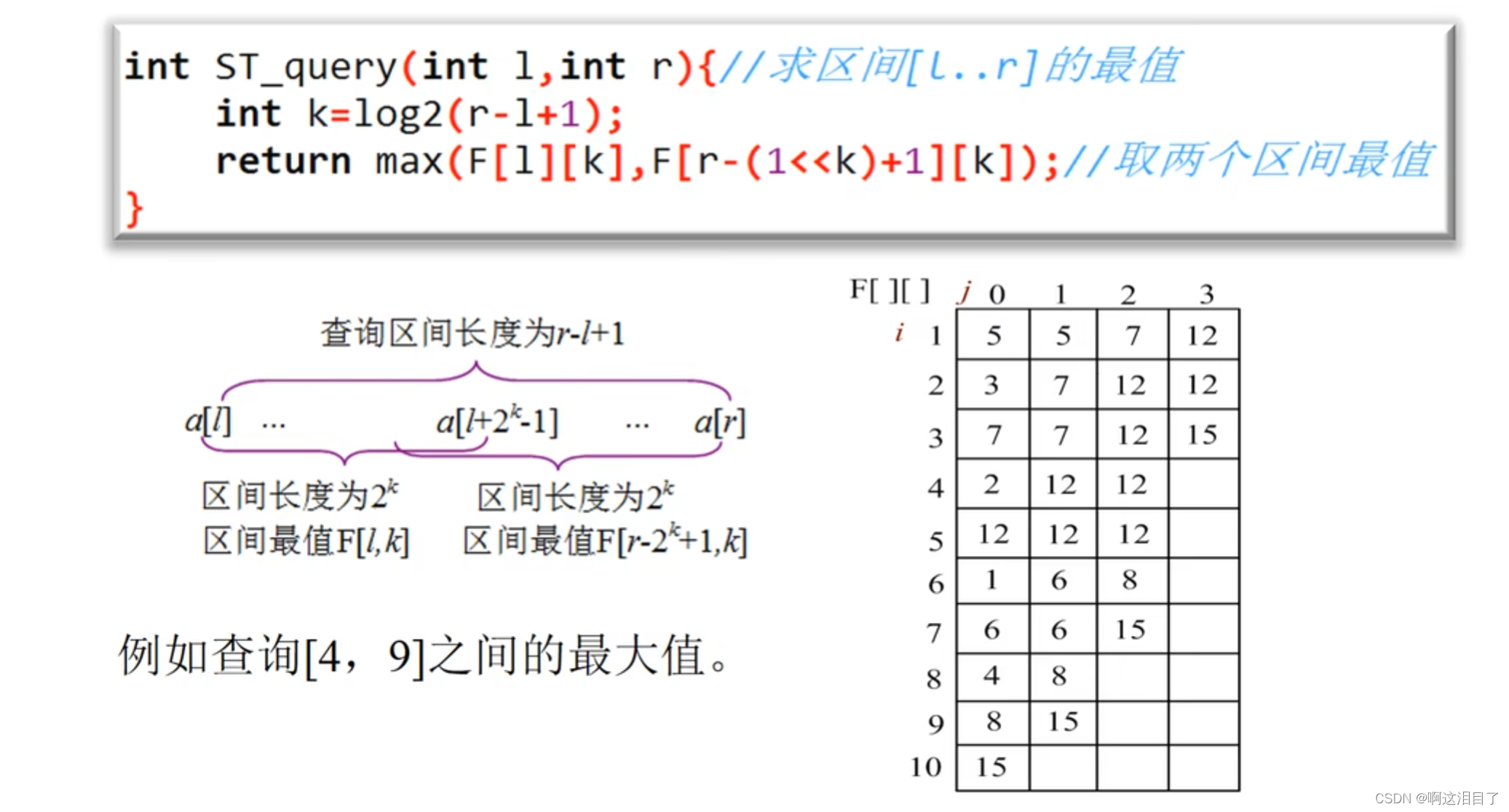
思路:主要只有预处理和查询两个重要的阶段,这是基于动态规划的思想,我们先建立一个二维的数组,命名为st,即st[i][j],这里的定义为以索引i为左端点,距离为2^j次的最大(最小)值为st[i][j]
以下是一个例子:

所以构建的st表如下:
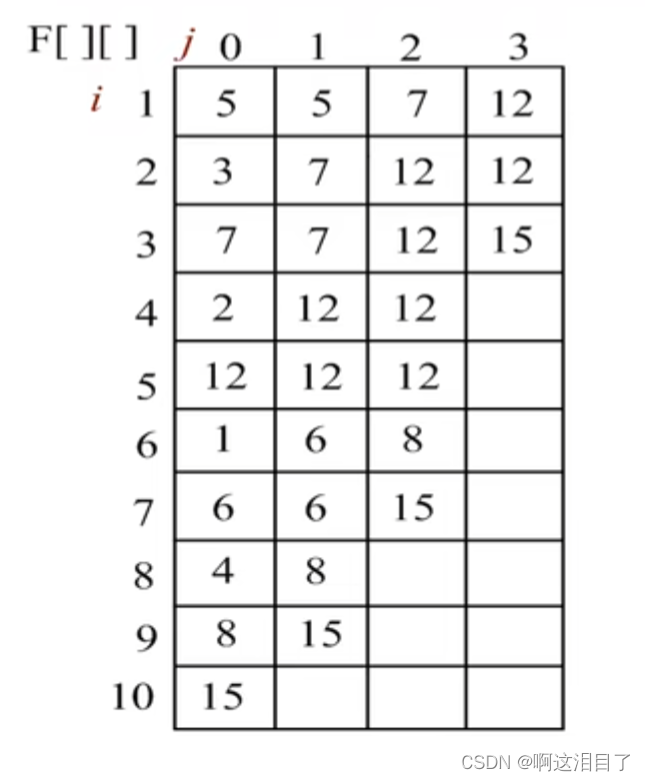
首先初始化st表:这里的定义为在以i为端点距离为1的区间内的最值就是它本身。
for (int i=1;i<=n;++i) st[i][0]=read();预处理:O(nlogn) 这里的18是给定数组大小的对数
for (int j=1;j<=18;++j){for (int i=1;i+(1<<(j-1))-1<=n;++i){st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);}}这里的预处理,不是一行一行下去的,是一列一列
这个转移方程的思路是:将长度为2^j的数组分成两份,每分的长度是2^(j-1),比较两个区间的最大值,所以就得出了这个大区间的最大值
st[i+(1<<(j-1))][j-1]这里就是改变了端点,使得找的范围是第二个区间。
查询功能:
给定一个查询区间[l,r],找到一个长度x,x<(r-l+1),然后继续上述的思想,比较划分的两个区间的大小,如下图所示
for (int i=1;i<=m;++i){int l=read(),r=read();int x=__lg(r-l+1);printf("%d\n", max(st[l][x], st[r - (1 << x) + 1][x]));} 所以就可以得到完整的AC代码
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3finline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
} const int N=1e5+5;int n,m,st[N][18];signed main(){n=read(),m=read();for (int i=1;i<=n;++i) st[i][0]=read();//预处理for (int j=1;j<=18;++j){for (int i=1;i+(1<<(j-1))-1<=n;++i){st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);}}//查询for (int i=1;i<=m;++i){int l=read(),r=read();int x=__lg(r-l+1);printf("%d\n", max(st[l][x], st[r - (1 << x) + 1][x]));}
}Balanced Lineup Ghttps://www.luogu.com.cn/problem/P2880
题目描述
For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 180,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.
每天,农夫 John 的 �(1≤�≤5×104)n(1≤n≤5×104) 头牛总是按同一序列排队。
有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊,牛的身高不应该相差太大。John 准备了 �(1≤�≤1.8×105)q(1≤q≤1.8×105) 个可能的牛的选择和所有牛的身高 ℎ�(1≤ℎ�≤106,1≤�≤�)hi(1≤hi≤106,1≤i≤n)。他想知道每一组里面最高和最低的牛的身高差。
输入格式
Line 1: Two space-separated integers, N and Q.
Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i
Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.
第一行两个数 �,�n,q。
接下来 �n 行,每行一个数 ℎ�hi。
再接下来 �q 行,每行两个整数 �a 和 �b,表示询问第 �a 头牛到第 �b 头牛里的最高和最低的牛的身高差。
输出格式
Lines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.
输出共 �q 行,对于每一组询问,输出每一组中最高和最低的牛的身高差。
输入输出样例
输入 #1复制
6 3
1
7
3
4
2
5
1 5
4 6
2 2输出 #1复制
6
3
0
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3finline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
} const int N=5e4+5;int n,q,st1[N][18],st2[N][18];signed main(){n=read(),q=read();for (int i=1;i<=n;++i){st1[i][0]=st2[i][0]=read();}//预处理for (int j=1;j<=18;++j){for (int i=1;i+(1<<(j-1))-1<=n;++i){st1[i][j]=max(st1[i][j-1],st1[i+(1<<(j-1))][j-1]);st2[i][j]=min(st2[i][j-1],st2[i+(1<<(j-1))][j-1]);}}//查询for (int i=1;i<=q;++i){int l=read(),r=read();int x=__lg(r-l+1);int ma=max(st1[l][x],st1[r-(1<<x)+1][x]);int mi=min(st2[l][x],st2[r-(1<<x)+1][x]);cout<<ma-mi<<endl;}
} 最近公共祖先(LCA)https://www.luogu.com.cn/problem/P3379
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式
第一行包含三个正整数 �,�,�N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 �−1N−1 行每行包含两个正整数 �,�x,y,表示 �x 结点和 �y 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 �M 行每行包含两个正整数 �,�a,b,表示询问 �a 结点和 �b 结点的最近公共祖先。
输出格式
输出包含 �M 行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例
输入 #1复制
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5输出 #1复制
4
4
1
4
4说明/提示
对于 30%30% 的数据,�≤10N≤10,�≤10M≤10。
对于 70%70% 的数据,�≤10000N≤10000,�≤10000M≤10000。
对于 100%100% 的数据,1≤�,�≤5000001≤N,M≤500000,1≤�,�,�,�≤�1≤x,y,a,b≤N,不保证 �≠�a=b。
对于LCA问题:
步骤1:建树,建树过程中,需要把每个节点的深度找到,因为最近的祖先的深度一定是一样的
这里先通过链式前向星存图:
void add(int u,int v){e[++tot].from=u;e[tot].to=v;e[tot].next=head[u];head[u]=tot;
}通过DFS建树:
建树的过程有几点:
第一个循环中,i的大小要小于等于它本身节点的深度
第一个循环中的递推式表示的含义是:节点v向上走2^i个节点就等于了节点v先走了2^(i-1)个节点,然后再走了2^(i-1)个节点
void dfs(int v,int fa){dep[v]=dep[fa]+1;f[v][0]=fa;for (int i=1;(1<<i)<=dep[v];++i){f[v][i]=f[f[v][i-1]][i-1];}for (int i=head[v];i;i=e[i].next){int p=e[i].to;if (p==fa) continue;dfs(p,v);}
}查询功能:
int LCA(int x,int y){if (dep[x]<dep[y]) swap(x,y); //规定x的深度要大于yfor (int i=20;i>=0;--i){ //x向上找节点,直到深度与y相同if (dep[f[x][i]]>=dep[y]) x=f[x][i];if (x==y) return x;}
/*
//等价
while(dep[x] > dep[y]){x=f[x][__lg(dep[x]-dep[y]-1)];}if (x==y) return x;
*/for (int i=20;i>=0;--i){ //x,y一起共同的向上找祖先,这里是从上向下找if (f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3finline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
} const int N=5e5+5;struct edge{int from;int to;int next;
}e[N*2];int n,m,s,f[N][25],tot,head[N],dep[N];void add(int u,int v){e[++tot].from=u;e[tot].to=v;e[tot].next=head[u];head[u]=tot;
}void dfs(int v,int fa){dep[v]=dep[fa]+1;f[v][0]=fa;for (int i=1;(1<<i)<=dep[v];++i){f[v][i]=f[f[v][i-1]][i-1];}for (int i=head[v];i;i=e[i].next){int p=e[i].to;if (p==fa) continue;dfs(p,v);}
}int LCA(int x,int y){if (dep[x]<dep[y]) swap(x,y);for (int i=20;i>=0;--i){if (dep[f[x][i]]>=dep[y]) x=f[x][i];if (x==y) return x;}for (int i=20;i>=0;--i){if (f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}signed main(){n=read(),m=read(),s=read();for (int i=0;i<n-1;++i){int u=read(),v=read();add(u,v);add(v,u);}dfs(s,0);for (int i=0;i<m;++i){int a=read(),b=read();cout<<LCA(a,b)<<endl;}
}景区导游https://www.dotcpp.com/oj/problem3156.html
题目描述
某景区一共有 N 个景点,编号 1 到 N。景点之间共有 N − 1 条双向的摆渡车线路相连,形成一棵树状结构。在景点之间往返只能通过这些摆渡车进行,需要花费一定的时间。
小明是这个景区的资深导游,他每天都要按固定顺序带客人游览其中 K 个景点:A1, A2, . . . , AK。今天由于时间原因,小明决定跳过其中一个景点,只带游客按顺序游览其中 K − 1 个景点。具体来说,如果小明选择跳过 Ai,那么他会按顺序带游客游览 A1, A2, . . . , Ai−1, Ai+1, . . . , AK, (1 ≤ i ≤ K)。
请你对任意一个 Ai,计算如果跳过这个景点,小明需要花费多少时间在景点之间的摆渡车上?
输入格式
第一行包含 2 个整数 N 和 K。
以下 N − 1 行,每行包含 3 个整数 u, v 和 t,代表景点 u 和 v 之间有摆渡车线路,花费 t 个单位时间。
最后一行包含 K 个整数 A1, A2, . . . , AK 代表原定游览线路。
输出格式
输出 K 个整数,其中第 i 个代表跳过 Ai 之后,花费在摆渡车上的时间。
样例输入
复制
6 4
1 2 1
1 3 1
3 4 2
3 5 2
4 6 3
2 6 5 1样例输出
复制
10 7 13 14
提示
原路线是 2 → 6 → 5 → 1。
当跳过 2 时,路线是 6 → 5 → 1,其中 6 → 5 花费时间 3 + 2 + 2 = 7,5 → 1 花费时间 2 + 1 = 3,总时间花费 10。
当跳过 6 时,路线是 2 → 5 → 1,其中 2 → 5 花费时间 1 + 1 + 2 = 4,5 → 1 花费时间 2 + 1 = 3,总时间花费 7。
当跳过 5 时,路线是 2 → 6 → 1,其中 2 → 6 花费时间 1 + 1 + 2 + 3 = 7,6 → 1 花费时间 3 + 2 + 1 = 6,总时间花费 13。
当跳过 1 时,路线时 2 → 6 → 5,其中 2 → 6 花费时间 1 + 1 + 2 + 3 = 7,6 → 5 花费时间 3 + 2 + 2 = 7,总时间花费 14。
对于 20% 的数据,2 ≤ K ≤ N ≤ 102。
对于 40% 的数据,2 ≤ K ≤ N ≤ 104。
对于 100% 的数据,2 ≤ K ≤ N ≤ 105,1 ≤ u, v, Ai ≤ N,1 ≤ t ≤ 105。保证Ai 两两不同。
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3finline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
} const int N=5e5+5;struct edge{int from;int to;int next;int d;
}e[N*2];int n,m,s,f[N][20],tot,head[N],dep[N],dis[N],luxian[N];void add(int u,int v,int d){e[++tot].from=u;e[tot].d=d;e[tot].to=v;e[tot].next=head[u];head[u]=tot;
}void dfs(int v,int fa,int d){dep[v]=dep[fa]+1;f[v][0]=fa;dis[v]=d;for (int i=1;(1<<i)<=dep[v];++i){f[v][i]=f[f[v][i-1]][i-1];}for (int i=head[v];i;i=e[i].next){int p=e[i].to;if (p==fa) continue;dfs(p,v,dis[v]+e[i].d);}
}int LCA(int x,int y){if (dep[x]<dep[y]) swap(x,y);for (int i=__lg(n);i>=0;--i){if (dep[f[x][i]]>=dep[y]) x=f[x][i];if (x==y) return x;}for (int i=__lg(n);i>=0;--i){if (f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}int get(int x,int y){return dis[x]+dis[y]-2*dis[LCA(x,y)];
}signed main(){n=read(),m=read();for (int i=0;i<n-1;++i){int u=read(),v=read(),d=read();add(u,v,d);add(v,u,d);}dfs(1,0,0);for (int i=1;i<=m;++i){luxian[i]=read();}int sum=0;for (int i=1;i<m;++i){sum+=get(luxian[i],luxian[i+1]);}for (int i=1;i<=m;++i){int ans=sum;if (i!=1) ans-=get(luxian[i],luxian[i-1]);if (i!=m) ans-=get(luxian[i],luxian[i+1]);if (i!=1 && i!=m) ans+=get(luxian[i-1],luxian[i+1]);cout<<ans<<" ";}
}