面试经典150题 -- 二叉树搜索树 (总结)

总的链接 :

https://leetcode.cn/studyplan/top-interview-150/

二叉搜索树相关概念 :

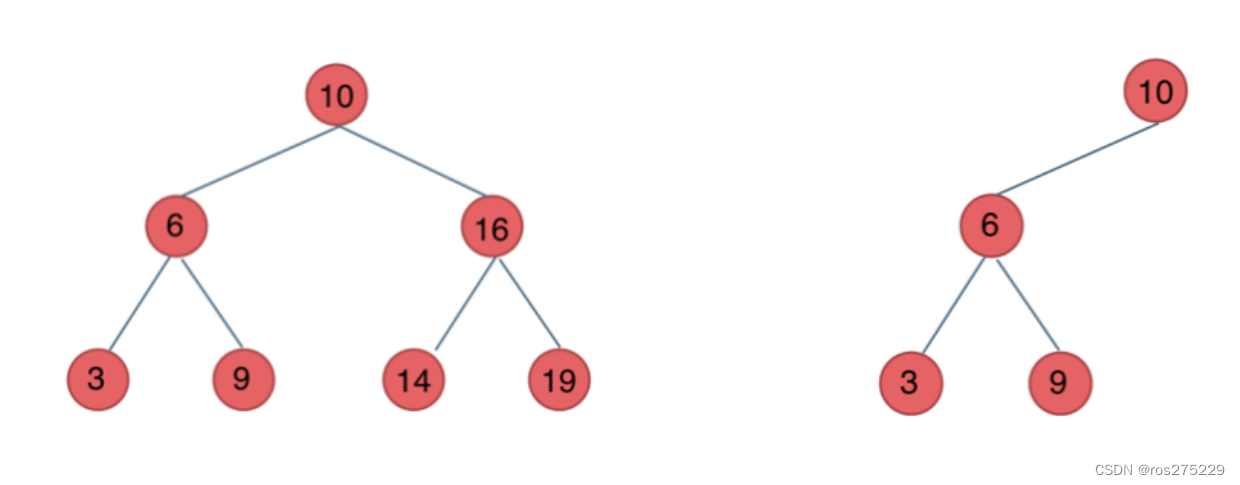
二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树;

如下图所示 : 两颗都是搜索树

530 . 二叉搜索树的最小绝对差

. - 力扣（LeetCode）

本题与下题相同 :

. - 力扣（LeetCode）

递归1

根据二叉搜索树的特点，左 < 根 < 右 , 使用中序遍历可以得到一个包含所有结点值得从小到大得有序数组 ;

然后遍历这个得到得数组，依次更新ans = min (ans , res[i] - res[i-1]) ;即可 ;

class Solution {
public:vector<int> res ;void dfs(TreeNode* root){if(root == nullptr) return ;dfs(root->left) ;res.push_back(root->val);dfs(root->right);}int getMinimumDifference(TreeNode* root) {int ans = INT_MAX ;dfs(root) ;for(int i=1;i<res.size();i++){ans = min(ans , res[i] - res[i-1]);}return ans ;}
};

递归2

其实在递归得过程中，可以借助一个pre结点表示当前结点得上一个结点，那么就不需要再创建一个数组来存了，直接在遍历得过程中，更新答案即可 ;

class Solution {
public:int ans = INT_MAX ;TreeNode* pre = nullptr ;void dfs(TreeNode* root){if(root == nullptr) return ;dfs(root->left) ;if(pre!=nullptr){ans = min(ans , root->val - pre->val);}pre = root ;dfs(root->right);}int getMinimumDifference(TreeNode* root) {dfs(root) ;return ans ;}
};

230 . 二叉搜索树中第k小的元素

递归(中序遍历)

用中序遍历得到一个排好序的存放所有节点值的数组，然后输出第k个元素即可 ;

class Solution {
public:vector<int> res ;void dfs(TreeNode* root){if(root == nullptr) return ;dfs(root->left) ;res.push_back(root->val);dfs(root->right);}int kthSmallest(TreeNode* root, int k) {dfs(root);return res[k-1] ;}
};

递归2 :

找到第k个，直接返回即可，不用存数组 ;

class Solution {
public: int t = 0 ;TreeNode* ans ;void dfs(TreeNode* root,int k){if(root == nullptr) return ;dfs(root->left,k) ;if(++t==k){ans = root ;return  ;}dfs(root->right,k);}int kthSmallest(TreeNode* root, int k) {dfs(root,k);return ans->val;}
};

98 . 验证二叉搜索树

用中序遍历得到结点值数组，判断该数组是否有序即可;

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> vc;void traversal(TreeNode* root){if(!root) return;traversal(root->left);vc.push_back(root->val);traversal(root->right);}bool isValidBST(TreeNode* root) {vc.clear();traversal(root);for(int i=1;i<vc.size();i++){if(vc[i] <= vc[i-1]) return false;}return true;}
};