530.二叉搜索树的最小绝对差 

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

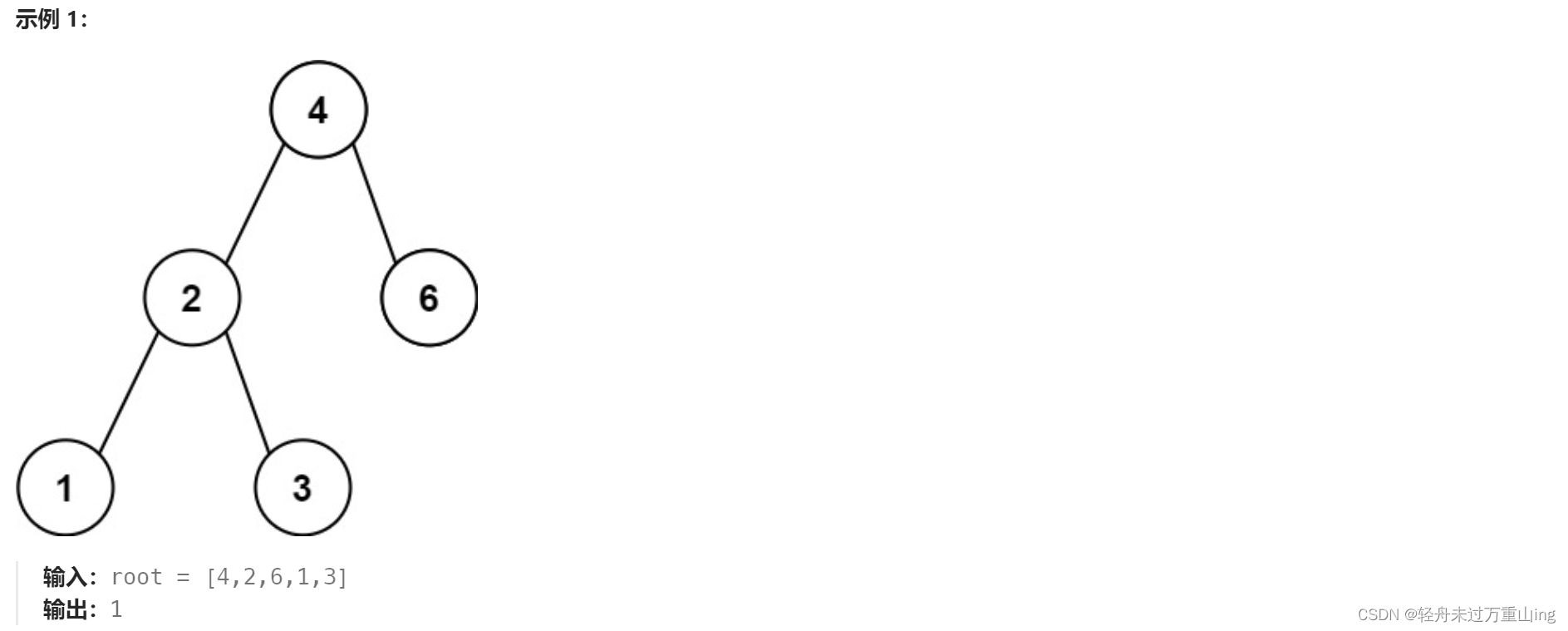
思路

题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。

注意是【二叉搜索树】，二叉搜索树可是有序的。

遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值，这样就简单多了。

#递归

那么二叉搜索树采用中序遍历，其实就是一个有序数组。

在一个有序数组上求两个数最小差值，这是不是就是一道送分题了。

最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。

....

以上代码是把二叉搜索树转化为有序数组了，其实在二叉搜素树中序遍历的过程中，我们就可以直接计算了。

需要用一个pre节点记录一下cur节点的前一个节点。

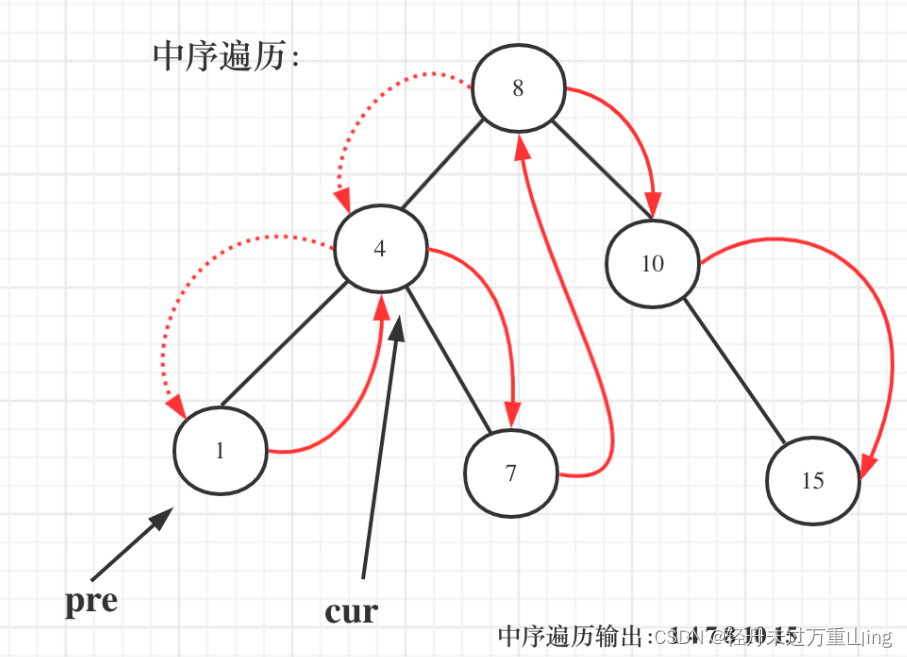
一些同学不知道在递归中如何记录前一个节点的指针，其实实现起来是很简单的，大家只要看过一次，写过一次，就掌握了。

class Solution {TreeNode pre = null; // 全局变量pre，记录上一个遍历的节点int result = Integer.MAX_VALUE; // 初始化结果为整数的最大值public int getMinimumDifference(TreeNode root) {if(root == null) return 0; // 如果根节点为空，直接返回 0traversal(root); // 开始中序遍历return result;  // 返回最小差值}public void traversal(TreeNode root){if(root == null) return ;  // 若当前节点为空，直接返回//左traversal(root.left);   // 递归遍历左子树//中if(pre != null){  // 计算当前节点值和上一个节点值的差值，更新结果result = Math.min(result,root.val - pre.val);}pre = root; // 更新上一个节点pre为当前节点root//右traversal(root.right);}
}

总结

遇到在二叉搜索树上求什么最值，求差值之类的，都要思考一下二叉搜索树可是有序的，要利用好这一特点。

同时要学会在递归遍历的过程中如何记录前后两个指针，这也是一个小技巧，学会了还是很受用的。

后面我将继续介绍一系列利用二叉搜索树特性的题目。

501.二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

• 结点左子树中所含节点的值 小于等于 当前节点的值
• 结点右子树中所含节点的值 大于等于 当前节点的值
• 左子树和右子树都是二叉搜索树

思路

这道题目呢，递归法我从两个维度来讲。

首先如果不是二叉搜索树的话，应该怎么解题，是二叉搜索树，又应该如何解题，两种方式做一个比较，可以加深大家对二叉树的理解。

#递归法

#如果不是二叉搜索树

如果不是【二叉搜索树】，最直观的方法一定是把这个树都遍历了，用map统计频率，把频率排个序，最后取前面高频的元素的集合。

具体步骤如下：

1. 这个树都遍历了，用map统计频率

至于用前中后序哪种遍历也不重要，因为就是要全遍历一遍，怎么个遍历法都行，层序遍历都没毛病！这里采用前序遍历，代码如下：

// map<int, int> key:元素，value:出现频率
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历if (cur == NULL) return ;map[cur->val]++; // 统计元素频率searchBST(cur->left, map);searchBST(cur->right, map);return ;
}

        2.把统计得出来的出现频率（即map中的value）排个序

有的同学可能可以想直接对map中的value排序，还真做不到，C++中如果使用std::map或者std::multimap可以对key排序，但不能对value排序。

所以要把map转化数组即vector，再进行排序，当然vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率。

bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {return a.second > b.second; // 按照频率从大到小排序
}vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序

        3.取前面高频的元素

此时数组vector中已经是存放着按照频率排好序的pair，那么把前面高频的元素取出来就可以了。

result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {// 取最高的放到result数组中if (vec[i].second == vec[0].second) result.push_back(vec[i].first);else break;
}
return result;

所以如果本题没有说是二叉搜索树的话，那么就按照上面的思路写！

方法一：针对一般的普通二叉树的 暴力法（有点难）

import java.util.*;
import java.util.stream.*;class Solution {public int[] findMode(TreeNode root) {//创建一个HashMap来统计每个节点值 出现的频率  Map<Integer,Integer> map  =  new HashMap<>();List<Integer> resList = new ArrayList<>();if(root == null) return resList.stream().mapToInt(Integer::intValue).toArray();//调用辅助递归函数来统计每个节点值出现的频率searchBST(root,map);//将频率 Map 转换为 List，按照值（出现的频率）降序排列List<Map.Entry<Integer,Integer>> mapList = map.entrySet().stream().sorted((c1,c2) -> c2.getValue().compareTo(c1.getValue())).collect(Collectors.toList());//将出现频率最高的节点值加入结果列表resList.add(mapList.get(0).getKey());//将出现频率相同的节点值加入结果列表for(int i = 1;i < mapList.size(); i ++){if(mapList.get(i).getValue() == mapList.get(i - 1).getValue()) {resList.add(mapList.get(i).getKey());}else{break;}}return resList.stream().mapToInt(Integer::intValue).toArray();}//辅助函数，用于递归地统计每个节点值出现的频率void searchBST(TreeNode root,Map<Integer,Integer> map){if(root == null) return; //如果当前节点为空，直接返回//更新节点值出现的频率map.put(root.val,map.getOrDefault(root.val,0) + 1);//递归地统计左子树和 右子树的节点值 出现的频率 searchBST(root.left,map);searchBST(root.right,map);}
}

补充说明：

①list.stream().mapToInt(Integer::intValue).toArray();

• 这行代码将 List 中的元素转换为整数流（Stream<Integer>），然后使用 mapToInt 方法将流中的每个 Integer 元素转换为对应的 int 值，最后使用 toArray 方法将转换后的 int 值存储到一个新的 int 数组中。

②List<Map.Entry<Integer, Integer>> mapList = map.entrySet().stream() .sorted((c1, c2) -> c2.getValue().compareTo(c1.getValue())) .collect(Collectors.toList());

• 使用 entrySet() 方法将 Map 转换为一个包含键值对的 Set。
• 调用 stream() 方法将 Set 转换为一个流（Stream<Map.Entry<Integer, Integer>>），其中每个元素是一个键值对（Map.Entry<Integer, Integer>）。
• 使用 sorted() 方法对流中的元素进行排序。在这里，使用的排序规则是按照键值对的值（频率）降序排列。这里使用了一个 Lambda 表达式 (c1, c2) -> c2.getValue().compareTo(c1.getValue())，它表示按照键值对的值从大到小排序。
• 最后使用 collect() 方法将排序后的流转换为一个 List，其中每个元素是一个排好序的键值对。

③map.put(cur.val, map.getOrDefault(cur.val, 0) + 1);

这行代码的作用是更新 map 中键为 cur.val 的值对应的频率。具体来说：

• 如果 map 中已经包含了键为 cur.val 的值，那么就将其对应的值加 1，并更新到 map 中。
• 如果 map 中不包含键为 cur.val 的值，那么使用 getOrDefault 方法获取到的默认值为 0，再加 1，并将结果更新到 map 中。

#如果是【二叉搜索树】

既然是搜索树，它中序遍历就是有序的。

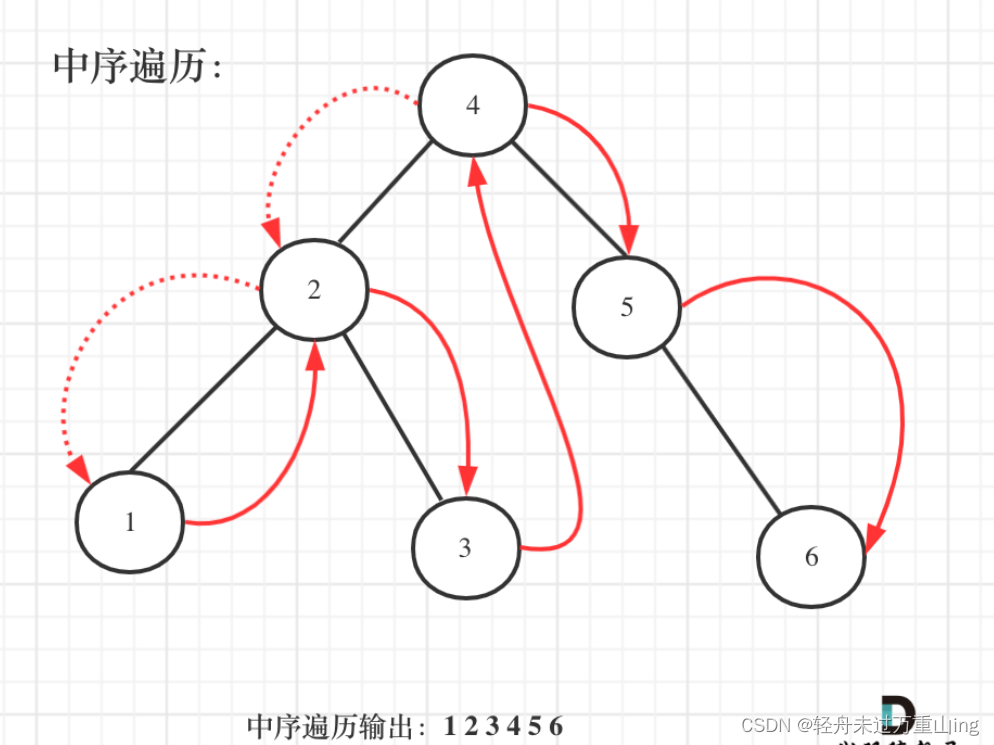
中序遍历代码如下：

void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);       // 左（处理节点）                // 中searchBST(cur->right);      // 右return ;
}

遍历有序数组的元素出现频率，从头遍历，那么一定是相邻两个元素作比较，然后就把出现频率最高的元素输出就可以了。

关键是在有序数组上的话，好搞，在树上怎么搞呢？

这就考察对树的操作了。

在二叉树：搜索树的最小绝对差 (opens new window)中我们就使用了pre指针和cur指针的技巧，这次又用上了。

弄一个指针指向前一个节点，这样每次cur（当前节点）才能和pre（前一个节点）作比较。

而且初始化的时候pre = NULL，这样当pre为NULL时候，我们就知道这是比较的第一个元素。

代码如下：

if (pre == NULL) { // 第一个节点count = 1; // 频率为1
} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;
} else { // 与前一个节点数值不同count = 1;
}
pre = cur; // 更新上一个节点

此时又有问题了，因为要求最大频率的元素集合（注意是集合，不是一个元素，可以有多个众数），如果是数组上大家一般怎么办？

应该是先遍历一遍数组，找出最大频率（maxCount），然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合。（因为众数有多个）

这种方式遍历了两遍数组。

那么我们遍历两遍二叉搜索树，把众数集合算出来也是可以的。

但这里其实只需要遍历一次就可以找到所有的众数。

那么如何只遍历一次呢？

如果 频率count 等于 maxCount（最大频率），当然要把这个元素加入到结果集中（以下代码为result数组），代码如下：

if (count == maxCount) { // 如果和最大值相同，放进result中result.push_back(cur->val);
}

是不是感觉这里有问题，result怎么能轻易就把元素放进去了呢，万一，这个maxCount此时还不是真正最大频率呢。

所以下面要做如下操作：

频率count 大于 maxCount的时候，不仅要更新maxCount，而且要清空结果集！（以下代码为result数组），因为结果集之前的元素都失效了，说明之前结果集里的都不是众数。

if (count > maxCount) { // 如果计数大于最大值maxCount = count;   // 更新最大频率result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了result.push_back(cur->val);
}

关键代码都讲完了，完整代码如下：（只需要遍历一遍二叉搜索树，就求出了众数的集合）

class Solution {//法二：中序遍历-不使用额外空间，利用二叉搜索树特性ArrayList<Integer> resList; //存放符合条件的众数 结果的列表int maxCount; //最大出现次数int count;  //当前节点值出现的次数TreeNode pre;  //前一个遍历的节点public int[] findMode(TreeNode root) {//初始化 成员变量resList =  new ArrayList<>();maxCount = 0;count = 0;pre = null;//开始遍历二叉搜索树（中序遍历）traversal(root);//将结果列表转化为 数组int[] res = new int[resList.size()];for(int i=0; i < resList.size(); i ++){res[i] = resList.get(i);}//返回结果数组resreturn res;}//定义递归方法traversal （中序）遍历搜索二叉树public void traversal(TreeNode root){if (root == null) {return; // 如果当前节点为空，直接返回}//递归遍历左子树traversal(root.left);int rootValue = root.val;//计数if(pre == null || rootValue != pre.val){ //pre==null，说明这是比较的第一个元素count = 1; //如果当前节点与上一个节点值不相同，计数为1}else{count++;  //否则，当前节点值=上一个节点值，计数加1}//更新结果以及maxCountif(count > maxCount){resList.clear(); //如果当前节点值出现次数大于最大出现次数，清空结果列表resList.add(rootValue); //将当前节点值加入结果列表 maxCount = count; //更新最大出现次数 }else if(count == maxCount){resList.add(rootValue);//如果当前节点值出现次数等于最大出现次数，将当前节点值加入结果列表}pre = root;  //更新上一个节点pre为当前节点 //递归遍历右子树traversal(root.right);}       
}

总结

本题在递归法中，我给出了如果是普通二叉树，应该怎么求众数。

知道了普通二叉树的做法时候，我再进一步给出二叉搜索树又应该怎么求众数，这样鲜明的对比，相信会对二叉树又有更深层次的理解了。

在递归遍历二叉搜索树的过程中，我还介绍了一个统计最高出现频率元素集合的技巧， 要不然就要遍历两次二叉搜索树才能把这个最高出现频率元素的集合求出来。

为什么没有这个技巧一定要遍历两次呢？ 因为要求的是集合，会有多个众数，如果规定只有一个众数，那么就遍历一次稳稳的了。

最后我依然给出对应的迭代法，其实就是迭代法中序遍历的模板加上递归法中中间节点的处理逻辑，分分钟就可以写出来，中间逻辑的代码我都是从递归法中直接粘过来的。

236. 二叉树的最近公共祖先  

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

思路

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

那么二叉树如何可以自底向上查找呢？

【回溯】啊，二叉树回溯的过程就是从低到上。

后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。

接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。 即情况一：

 判断逻辑是 如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果 左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。

那么有录友可能疑惑，会不会左子树 遇到q 返回，右子树也遇到q返回，这样并没有找到 q 和p的最近祖先。

这么想的录友，要审题了，题目强调：二叉树节点数值是不重复的，而且一定存在 q 和 p。

---但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q(p)。 情况二：

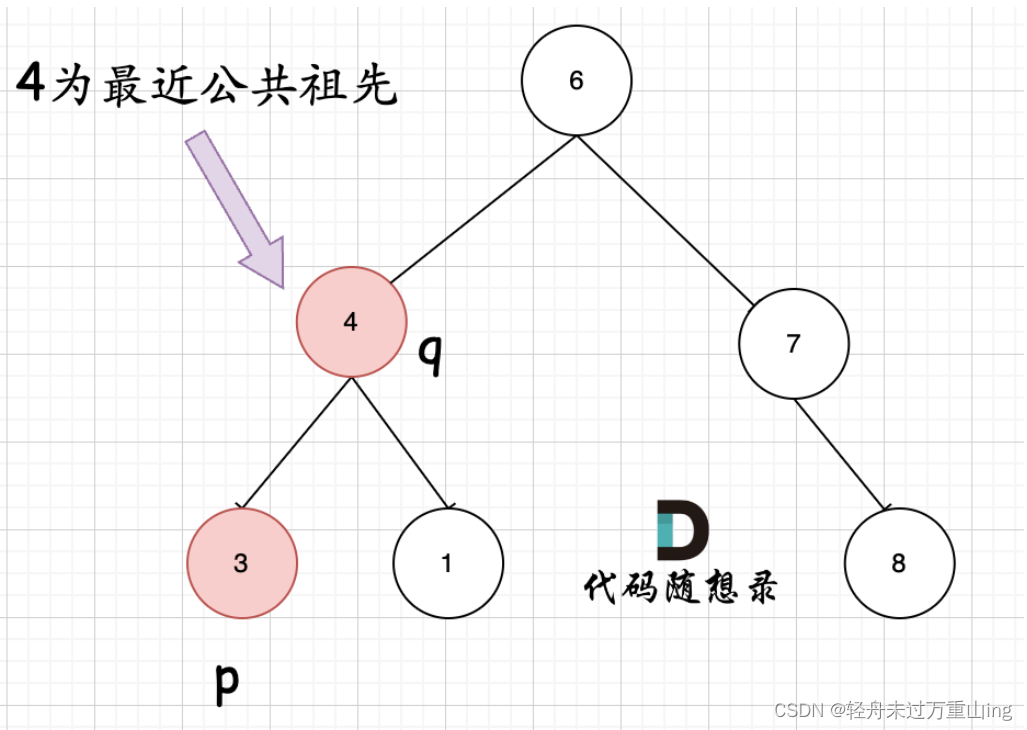
 其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。

因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。

这一点是很多录友容易忽略的，在下面的代码讲解中，可以再去体会。

递归三部曲：

• 确定递归函数返回值以及参数

需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。

但--我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)

• 确定单层递归逻辑

值得注意的是 本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。

我们在二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？ (opens new window)中说了 递归函数有返回值就是要遍历某一条边，但有返回值也要看如何处理返回值！

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：

if (递归函数(root->left)) return ;if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

看出区别了没？

在递归函数有返回值的情况下：

• 如果要搜索一条边，递归函数返回值不为空的时候，立刻返回；
• 如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。

 就像图中一样直接返回7。

但事实上还要遍历根节点右子树（即使此时已经找到了目标节点了），也就是图中的节点4、15、20。

因为在如下代码的后序遍历中，如果想利用left和right做逻辑处理， 不能立刻返回，而是要等left与right逻辑处理完之后才能返回。

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

所以此时大家要知道我们要遍历整棵树。知道这一点，对本题就有一定深度的理解了。

那么先用left和right接住左子树和右子树的返回值，代码如下：

TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);

如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解

如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之亦然！

这里有的同学就理解不了了，为什么left为空，right不为空，目标节点通过right返回呢？

如图：

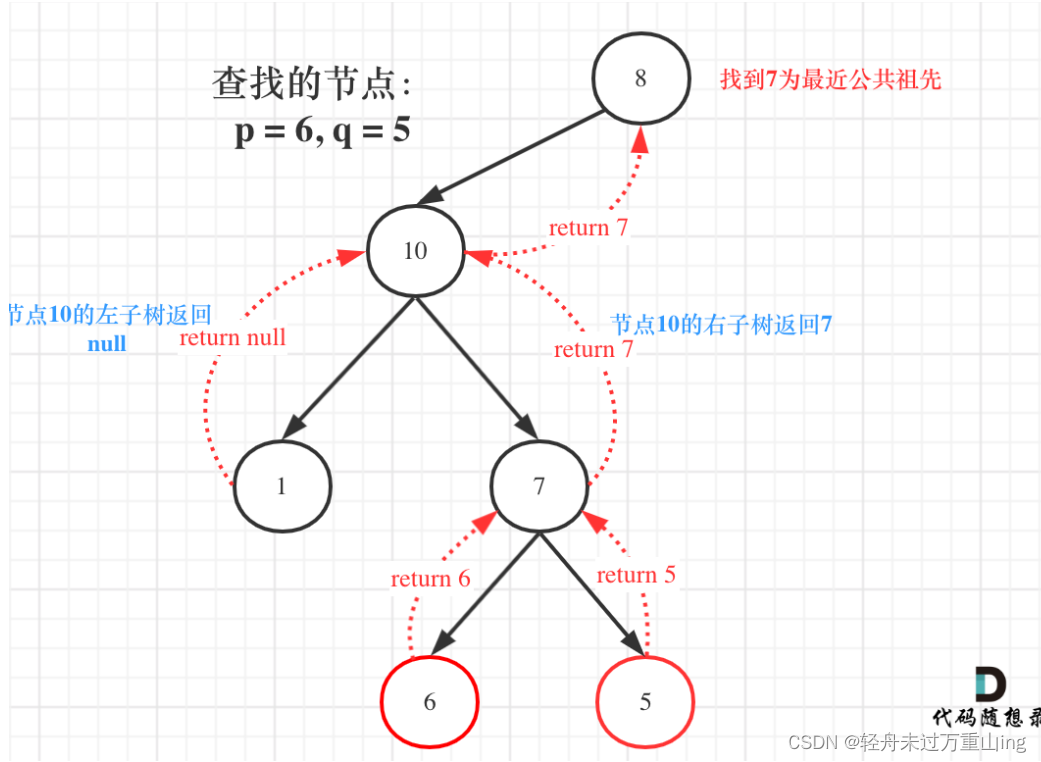
 图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

这里也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else  { //  (left == NULL && right == NULL)return NULL;
}

那么寻找最小公共祖先，完整流程图如下：

 从图中，可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 递归结束条件：如果根节点为空，或者根节点等于 p 或 q，则返回根节点if(root == null || root == p || root == q){return root;}//后序遍历：分别在左右子树中寻找p和q的最低公共祖先 TreeNode left = lowestCommonAncestor(root.left,p,q);  //【左】TreeNode right = lowestCommonAncestor(root.right,p,q); //【右】// 【中】//如果左右子树都没有找到p和q，则返回 null  if(left == null && right == null) {return null;}//如果只在右子树找到了一个节点，则返回右子树找到的节点 else if(left == null && right != null){return right;}//如果只在左子树找到了一个节点，则返回左子树找到的节点else if(left != null && right == null){return left;}//如果左右子树各找到一个节点，则当前节点就是它们的最近公共祖先else{return root;}}
}

总结

这道题目刷过的同学未必真正了解这里面回溯的过程，以及结果是如何一层一层传上去的。

那么我给大家归纳如下三点：

1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。

2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

3. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。

本题没有给出迭代法，因为迭代法不适合模拟回溯的过程。理解递归的解法就够了。