代码随想录算法训练营第39天| Leetcode 62.不同路径、Leetcode 63. 不同路径 II

文章目录

Leetcode 62.不同路径
Leetcode 63. 不同路径 II

Leetcode 62.不同路径

题目链接：Leetcode 62.不同路径
题目描述： 一个机器人位于一个 m x n 网格的左上角，机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。问总共有多少条不同的路径？
思路： 本题算是属于高中数学排列组合的基本问题，如果想从左上角移动到右下角，无论如何移动，整体上一定是向下移动m-1次，向右移动n-1次，一共移动m+n-2次，因此用数学表达式描述就是：

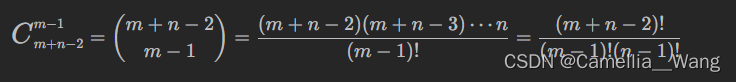
注：上述图片来源于Leetcode题解区
想了解更多排列组合的基础知识可以自行搜索，在这里不再赘述。

代码如下：（数学方法）

class Solution {
public:int uniquePaths(int m, int n) {long long result = 1;for (int x = n, y = 1; y < m; x++, y++) {result = result * x / y;}return result;}
};

时间复杂度： $O (min (m, n))$
空间复杂度： $O (1)$

当然本题还可以利用动态规划来解决：

定义dp[i][j] ：表示从（0 ，0）出发，到（i ，j） 有dp[i][j]条不同的路径。
求解dp[i][j]：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
初始化：dp[i][0]和dp[0][i]都可以从起点移动一次到达，因此初始化为1
结果：dp[m-1][n-1]

代码如下：（动态规划）

class Solution {
public:int uniquePaths(int m, int n) {int dp[m + 5][n + 5]; //防止数组越界for (int i = 0; i < n; i++)dp[0][i] = 1;for (int i = 0; i < m; i++)dp[i][0] = 1;for (int i = 1; i < m; i++)for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}return dp[m-1][n-1];}
};

时间复杂度： $O (m \times n)$
空间复杂度： $O (m \times n)$

（动态规划+滚动数组优化）

class Solution {
public:int uniquePaths(int m, int n) {int dp[n + 5]; //防止数组越界for (int i = 0; i < n; i++)dp[i] = 1;for (int i = 1; i < m; i++)for (int j = 1; j < n; j++) {dp[j] += dp[j - 1];}return dp[n - 1];}
};

时间复杂度： $O (m \times n)$
空间复杂度： $O (n)$

Leetcode 63. 不同路径 II

题目链接：Leetcode 63. 不同路径 II
题目描述： 一个机器人位于一个 m x n 网格的左上角 ,机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0来表示。
思路： 这道题就用不了数学方法了，因为不能确定障碍物挡住了多少路线，所以使用动态规划。

定义dp[i][j] ：表示从（0 ，0）出发，到（i ，j） 有dp[i][j]条不同的路径。
求解dp[i][j]：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，如果dp[i][j]为障碍物，则跳过本次循环
初始化：dp[i][0]和dp[0][i]都可以从起点移动一次到达，未被障碍物挡住的元素初始化为1
结果：dp[m-1][n-1]

代码如下：

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1)return 0; //起点和终点有障碍物则无路径vector<vector<int>> dp(m, vector<int>(n, 0));//初始化for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++)dp[0][i] = 1;for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)dp[i][0] = 1;//计算for (int i = 1; i < m; i++)for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1)continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}return dp[m - 1][n - 1];}
};