【寸铁的刷题笔记】树、dfs、bfs、回溯、递归(一)
大家好 我是寸铁👊
总结了一篇刷题关于树、dfs、bfs、回溯、递归的文章✨
喜欢的小伙伴可以点点关注 💝
105. 从前序与中序遍历序列构造二叉树
模拟分析图
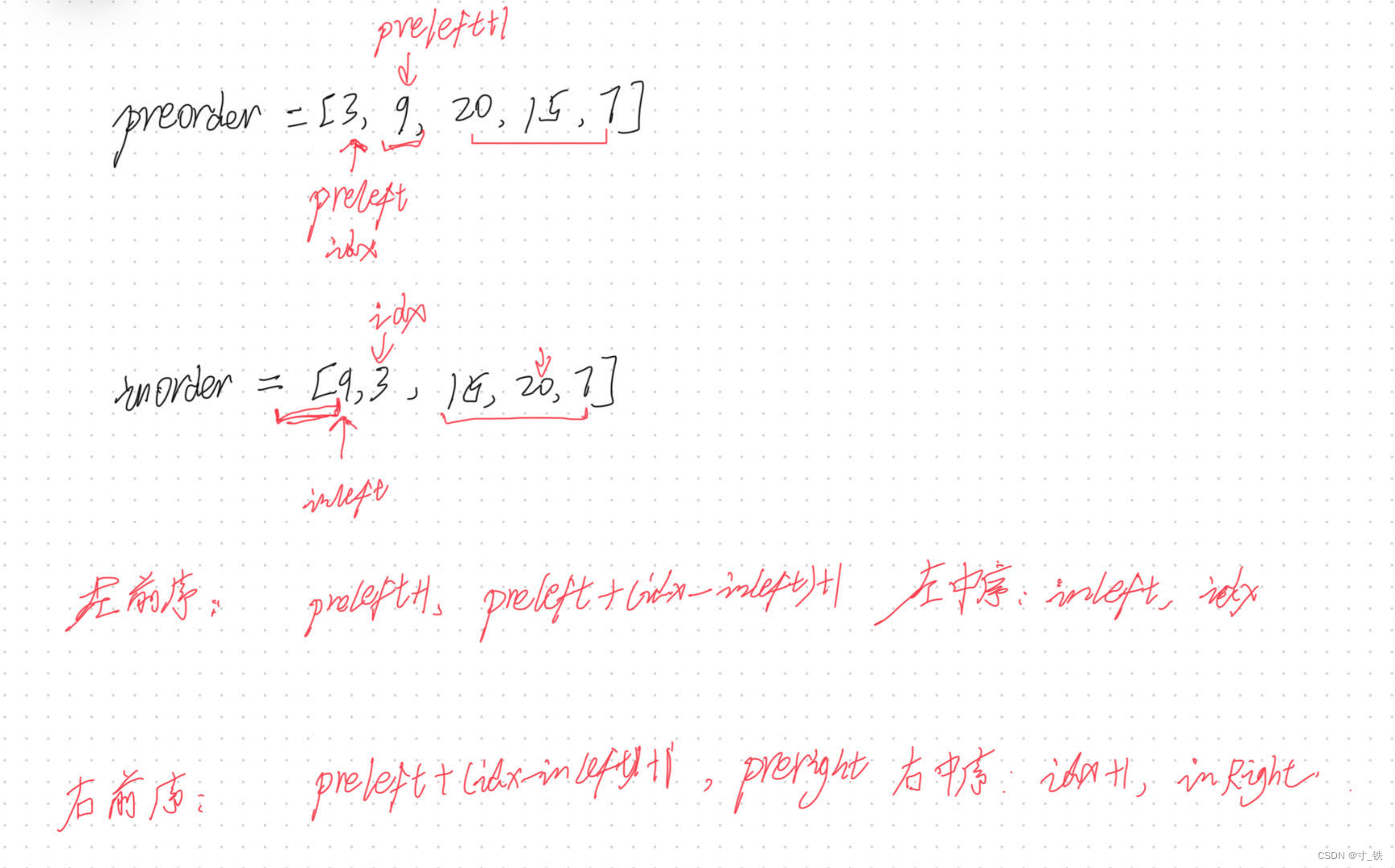
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTree1(preorder , 0 , preorder.length , inorder , 0 , inorder.length);}public TreeNode buildTree1(int []preorder , int preLeft, int preRight , int []inorder , int inLeft , int inRight){//递归终止条件//中序数组中右边界-左边界 < 1//返回nullif(inRight - inLeft < 1){return null;}//只有一个节点//则创建该值的节点返回出去即可if(inRight - inLeft == 1){return new TreeNode(inorder[inLeft]);}//前序遍历中的第一个值为根节点的值int Val = preorder[preLeft];//记录根节点的下标索引int rootIdx = 0;//在中序数组中查找到第一个值所在的下标//用于根据该下标进行数组的切割TreeNode root = new TreeNode(Val);for(int i = inLeft; i < inRight; i++){if(inorder[i] == Val){rootIdx = i;break;}}//递归根节点的左子树和右子树//注意: 编写递归时要统一规范//由于上面写的是i < inRight//这里需要不断查找每个切分的数组的根节点进行切割。//区间是左闭右开的 要统一规范去写//清楚是左闭右开后 编写逻辑如下:root.left = buildTree1(preorder , preLeft + 1 , preLeft + 1 + (rootIdx - inLeft) , inorder , inLeft , rootIdx);root.right = buildTree1(preorder , preLeft+1+(rootIdx - inLeft) , preRight , inorder , rootIdx + 1 , inRight);//返回最后的根节点//每次递归时,向上返回该节点,接住该节点的是左孩子或者右孩子return root;}
}106. 从中序与后序遍历序列构造二叉树
模拟分析图

代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {//注:传入的是中序和后序数组的长度//区间是左闭右开return buildTree1(inorder , 0 , inorder.length , postorder , 0 , postorder.length);}public TreeNode buildTree1(int []inorder , int inleft, int inRight , int[]postorder , int postLeft,int postRight){//对中序数组进行判断//如果说中序数组的长度 - 起点下标 < 1 //则说明没有元素 返回空// 0 - 0 = 0 < 1if(inRight - inleft < 1){return null;}//只有一个元素//则创建一个该元素的节点返回即可if(inRight - inleft == 1){return new TreeNode(inorder[inleft]);}//后序数组中的最后一个元素即为根起点int rootVal = postorder[postRight - 1];TreeNode root = new TreeNode(rootVal);int rootIndex = 0;//根据拿到的根节点root在中序数组中找到切割点for(int i = inleft; i < inRight; i++){if(inorder[i] == rootVal){rootIndex = i;}}//根据rootIndex在中、后序数组中划分左右子树//在中序中划分root.left = buildTree1(inorder , inleft , rootIndex, postorder , postLeft , postLeft + (rootIndex - inleft));//在后序中划分 root.right = buildTree1(inorder, rootIndex + 1, inRight , postorder , postLeft + (rootIndex - inleft) , postRight - 1); return root;}
}
112. 路径总和
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {//如果说根节点为空 则无法得到目标和 直接返回falseif(root == null) return false;//采用的是减法 看最后targetSum 减少到最后是否为0//递归调用 传入根节点 此时count和为targetSum - 当前根节点的值return traversal(root , targetSum - root.val);}public boolean traversal(TreeNode cur , int count){//如果说左子树和右子树都为空(此为叶子节点) 并且count等于0//则说明存在路径使得节点之和为targetSum//返回trueif(cur.left == null && cur.right == null && count == 0)return true;//否则返回falseif(cur.left == null && cur.right == null && count == 0)return false;//递归逻辑//递归左子树if(cur.left != null){//减去当前遍历到的节点值count -= cur.left.val;//注意:这里需要向上返回布尔值//如果往左子树遍历的结果为true//则向上返回trueif(traversal(cur.left , count)){return true;}//回溯 把之前减去的节点值加上//再从另一个分支去寻找是否存在路径count += cur.left.val;}//同理,递归右子树if(cur.right != null){count -= cur.right.val;if(traversal(cur.right , count)){return true;}count += cur.right.val;}return false;}
}113. 路径总和 II
相比较 112. 路径总和
113. 路径总和 II || 与下面的 129. 求根节点到叶节点数字之和
共同的逻辑都是需要遍历一棵树从根节点到所有叶子节点
这意味着需要一个数据结构(list)去存储所有经过的路径上的节点
也就意味着不需要返回值,但是由于需要遍历所有的叶子节点
这里需要进行向上回溯,也就是怎么来的就怎么去(恢复现场)
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//result队列用于接收满足条件的pathList<List<Integer>> result;//path用于接收每次搜索的结果//这里不用开启全局变量//原因:path会遍历到叶子节点会向上回溯 LinkedList<Integer> path;public List<List<Integer>> pathSum(TreeNode root, int targetSum) {result = new LinkedList<>();path = new LinkedList<>();travesal(root , targetSum);return result;}//这里由于有path接收搜索的结点//所以,这里不需要去返回值public void travesal(TreeNode root , int count){//如果说根节点为空 则直接结束if(root == null) return;//先把当前的节点值加入到path队列中path.offer(root.val);//然后,更新当前的count 把当前添加入队列的节点值减去count -= root.val;//接着,处理临界条件,也就是遍历到叶子节点对答案的判断if(root.left == null && root.right == null && count == 0){//满足条件则把当前遍历的节点添加到path队列中result.add(new LinkedList<>(path));}//向下递归,遍历左子树和右子树//这里是直接往左子树或者右子树的某个方向能走的路走到底//无论是往右还是左走 走到底即可//走到底无路可走后再向上回溯 依次移除最后一个元素 再去搜索其他分支travesal(root.left , count);travesal(root.right , count);path.removeLast();}
}
debug
class Solution {List<List<Integer>> result;LinkedList <Integer> path;public List<List<Integer>> pathSum(TreeNode root, int targetSum) {result = new LinkedList<>();path = new LinkedList<>();travesal(root , targetSum);return result;}public void travesal(TreeNode root , int count){if(root == null)return;path.offer(root.val);count -= root.val;System.out.println("111111111");System.out.println(path);if(root.left == null && root.right == null && count == 0){//打印出来去看path的变化过程System.out.println("22222222");System.out.println(path);result.add(new LinkedList<>(path));}travesal(root.left , count);System.out.println("leftleftleftleftleftleft");System.out.println(path);travesal(root.right , count);System.out.println("333333333333");System.out.println(path);//依次移除掉最后一个节点,向上回溯//直至移除到最后一个根节点path.removeLast();}
}
129. 求根节点到叶节点数字之和
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {//path存储dfs到的节点List<Integer>path = new LinkedList<>();//记录最终求和的结果int res = 0;public int sumNumbers(TreeNode root) {//如果root为null 则返回0if(root == null)return 0;//如果root不为null 则把根节点添加到path中path.add(root.val);travesal(root);return res;}public void travesal(TreeNode root){//遍历到叶子节点则对当前的path的值求和if(root.left == null && root.right == null){res += listToInt(path);}//遍历左子树if(root.left != null){//先添加左子树节点的值path.add(root.left.val);//再继续递归到下一层travesal(root.left);//移除掉当前队列中的最后一个元素 向上回溯path.remove(path.size() - 1);}//遍历右子树if(root.right != null){path.add(root.right.val);travesal(root.right);path.remove(path.size() - 1);}}//对path中存储的节点值进行求和public int listToInt(List<Integer> path){int sum = 0;//这里由于list是队列 先进先出//在原来的sum基础上乘10 再加上最后一个元素即可for(Integer s : path){sum = sum * 10 + s;}return sum;}}
总结
大逻辑其实还是最核心的三个点,一个是根节点,一个是左孩子 ,一个是右孩子。
可以把递归函数看成是一个整体部分,整体的去对左子树进行处理,整体
的去对右子树进行处理,然后返回结果或者说记录结果,不必去深究递归里面的细节,会让整个的解题思路变得十分复制混乱,就是理解为递归函数去帮助你进行处理,最后返回一个结果或者将结果存起来就好了!
看到这里的小伙伴,恭喜你又掌握了一个技能👊
希望大家能取得胜利,坚持就是胜利💪
我是寸铁!我们下期再见💕
往期好文💕
保姆级教程
【保姆级教程】Windows11下go-zero的etcd安装与初步使用
【保姆级教程】Windows11安装go-zero代码生成工具goctl、protoc、go-zero
【Go-Zero】手把手带你在goland中创建api文件并设置高亮
报错解决
【Go-Zero】Error: user.api 27:9 syntax error: expected ‘:‘ | ‘IDENT‘ | ‘INT‘, got ‘(‘ 报错解决方案及api路由注意事项
【Go-Zero】Error: only one service expected goctl一键转换生成rpc服务错误解决方案
【Go-Zero】【error】 failed to initialize database, got error Error 1045 (28000):报错解决方案
【Go-Zero】Error 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using password: YES)报错解决方案
【Go-Zero】type mismatch for field “Auth.AccessSecret“, expect “string“, actual “number“报错解决方案
【Go-Zero】Error: user.api 30:2 syntax error: expected ‘)‘ | ‘KEY‘, got ‘IDENT‘报错解决方案
【Go-Zero】Windows启动rpc服务报错panic:context deadline exceeded解决方案
Go面试向
【Go面试向】defer与time.sleep初探
【Go面试向】defer与return的执行顺序初探
【Go面试向】Go程序的执行顺序
【Go面试向】rune和byte类型的认识与使用
【Go面试向】实现map稳定的有序遍历的方式

![[linux]进程间通信(IPC)———共享内存(shm)(什么是共享内存,共享内存的原理图,共享内存的接口,使用演示)](https://img-blog.csdnimg.cn/direct/bc619ee07ca34a1cac56b6dae55988f1.png)