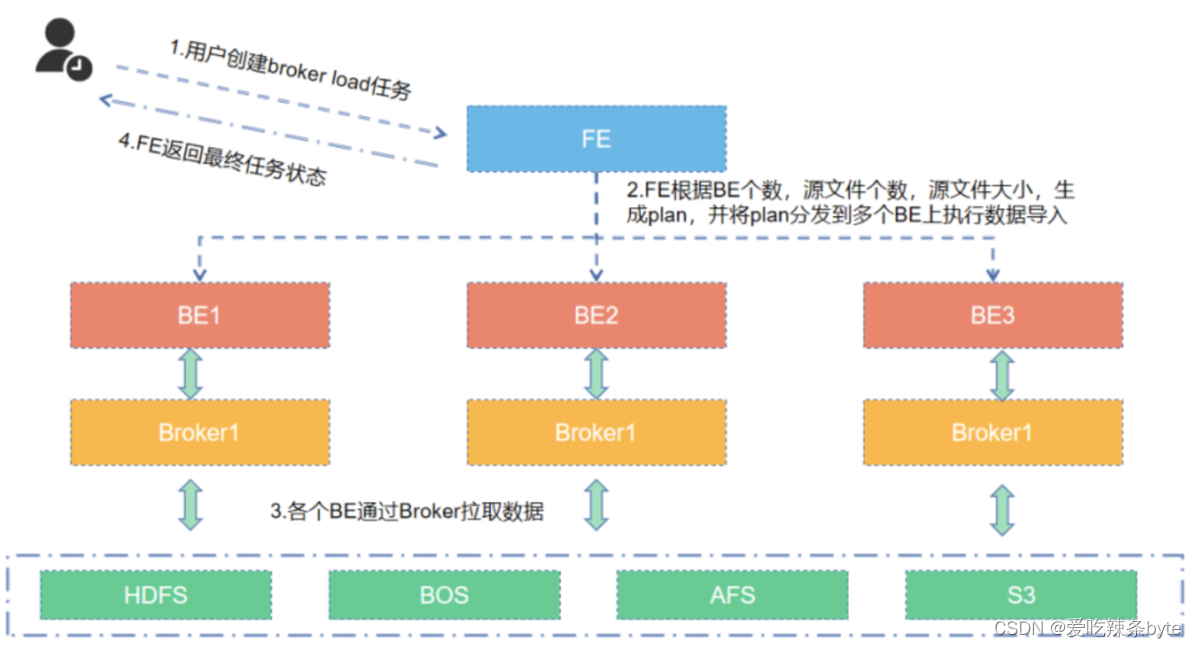
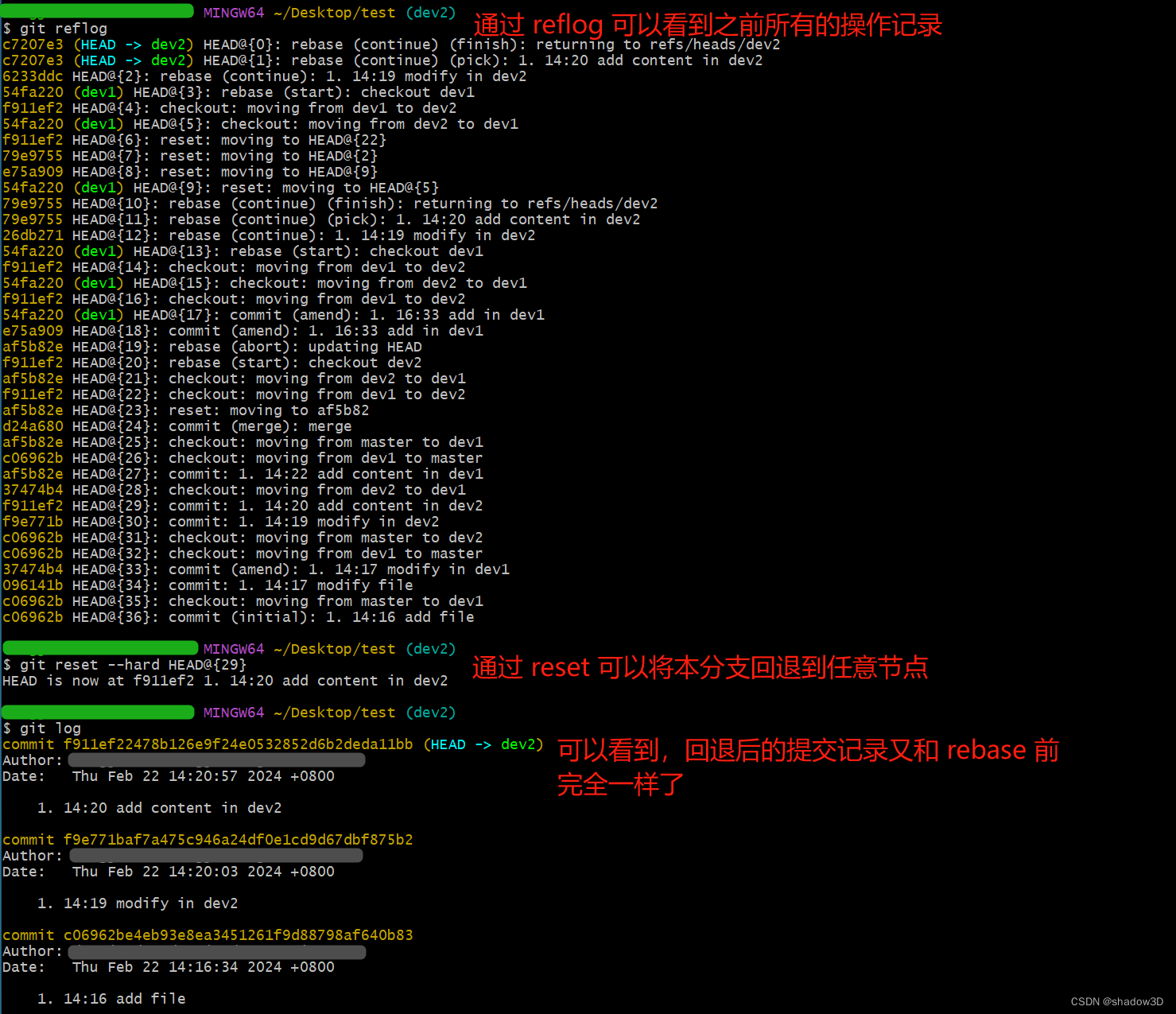
树-王道-复试

树

1.度： 树中孩子节点个数，所有结点的度最大值为树的度
2.有序树： 逻辑上看，树中结点的各子树从左至右是有次序的，不能互换。
**3.**树的根节点没有前驱，其他节点只有一个前驱
**4.**所有节点可有零个或者多个后继

常考性质

1. 节点数 = 总度数（总边数）+1
2.度为 m 的树、m 叉树的区别：
在这里插入图片描述
** 3. 度为m的数第 i 层至多有m^{(i-1)个结点，m叉树第i层至多有m}(i-1)个节点 **
**4.高度为 h 的 m 叉树至多:**有（m^h-1）/m-1个节点
5.高度为 h 的 m 叉树至少: h个节点
6.高度为 h、度为 m 的树至少: h+m-1个节点
7.最小高度为： logmn
在这里插入图片描述

最小高度的计算：

2.完全二叉树

就是右叶子节点为缺，左边都是连起来的
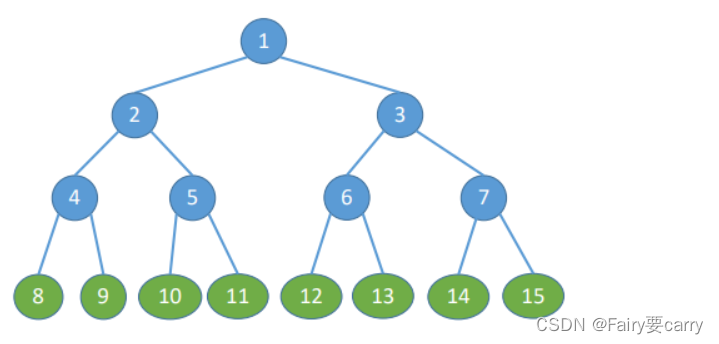
在这里插入图片描述
特点：

1.只有最后两层可能有叶子结点。
2最多只有一个度为 1 的结点。(屁股节点，也就是度为1的节点只有1个)
3若按层序从 1 开始编号，结点 i 的左孩子为 2i，右孩子为 2i+1；结点 i 的父节点为 ⌊ i / 2 ⌋ \lfloor i/2\rfloor⌊i/2⌋。
4 i ≤ ⌊ n / 2 ⌋ 为分支结点，i > ⌊ n / 2 ⌋ 为叶子结点。

3.平衡二叉树与二叉搜索树的区别：

平衡：树上任一结点的左子树和右子树的深度之差不超过 1。
搜索：左小于根，右大于根
https://blog.csdn.net/weixin_57128596/article/details/127216542?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522170853038416800185813532%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=170853038416800185813532&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_blogfirst_rank_ecpm_v1~rank_v31_ecpm-1-127216542-null-null.nonecase&utm_term=BST&spm=1018.2226.3001.4450

4.度合节点数的区别：

1.节点总数n=n0+n1+n2（度为0的节点数+度为1的节点数+度为2的节点数）
n0=n2+1（度为0的节点数=度为2的节点数+1）
2.二叉树的第i层至多有2的i-1次方个节点
3.高度为h的二叉树至多有2的h次方-1个节点
4.如果完全二叉树有2K个节点（偶数），则n1=1，n0=k，n2=k-1
5.如果完全二叉树有2K-1个节点（奇数），则n1=0，n0=k，n2=k-1

5.二叉树的左右孩子

1:节点i的左孩子为 2i
2:节点i的右孩子为 2i+1
3:节点i的父节点为【i/2】
4:节点i的层次为【log2(i+1)】

6.前中后序遍历

前序：
根左右
中序：
左根右
后序：
左右根

typedef struct BiNode{ElemType data;struct BiNode *lchild,*rchild;
}BiNode,*BiTree;void PreOrder(BiTree T){if(T!=NULL){visit(T);//访问根节点PreOrder(T->lChild);//递归左子树PreOrder(T->rChild);//递归右子树}
}void InOrder(BiTree T){if(T!=NULL){InOrder(T->lchild);//递归左子树visit(T);//访问当前节点InOrder(T->rchild);//递归右子树}
}void PostOrder(BiTree T){if(T!=NULL){PostOrder(T->lchild);//递归左子树PostOrder(T->lright);//递归右子树visit(T);}
}

求树的最大深度

int maxDepth(BiTree T){if(T==NULL) return 0;int lDepth=maxDepth(T->lchild);//当前节点的左子树深度int rDepth=maxDepth(T->rchild);//当前节点的右子树深度return lDepth>rDepth?lDepth+1:rDepth+1;
}

二叉树的层序遍历

//二叉树节点
typedef struct BiNode{ElemeType data;struct BiNode* lchild,*rchild;
}BiNode,*BiTree;
//链式队列节点，作层序
typedef struct LinkNode{BiNode* data;struct LinkNode* next;
}LinkNode;//层序集合，类似List<List<TreeNode>>
typedef struct{LinkNode *front,*rear;
}LinkQueue;void LevelOrder(BiTree T){LinkQueue Q; //类似List<List<TreeNode>>InitQueue(Q);BiTree p;//二叉树节点EnQueue(Q,T);//将T入到我们的队列Q中while(!IsEmpth(Q)){DeQueue(Q,p);//将队列中的队首元素出队，并将其赋值给 p，这样就可以访问当前节点 pvisit(p);//将节点的子节点入队if(p->lchild!=NULL){EnQueue(Q,p->lchild);}if(p->rchild!=NULL){EnQueue(Q,p->rchild);}}
}

7.中序前序后序的节点变换

8.树和森林题目

1.
1.：讨论二叉树高度，必须要说他是完全二叉树，高度为log2(n)+1
2.：树-一般我们阐述的是左孩子右兄弟树，左侧图，叶子节点树为1，对应二叉树-因为右兄弟，所以转为二叉树，有两个叶子节点
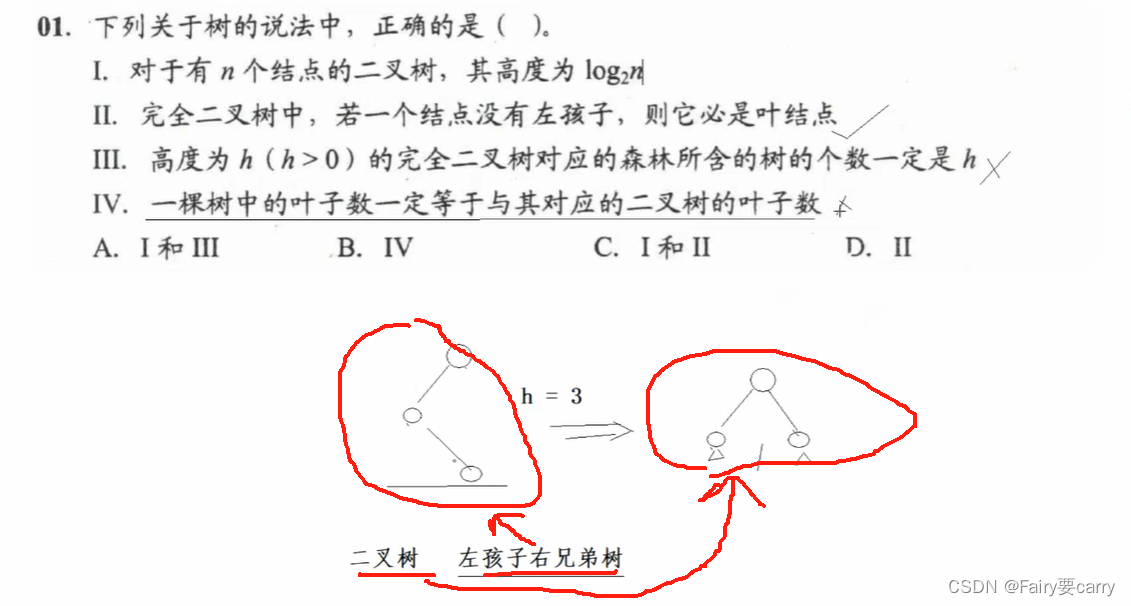
在这里插入图片描述

树转二叉树的规则：

左孩子右兄弟，BCD三个节点彼此就是兄弟，B是A的孩子，CD是B的兄弟，
但是有个从左到右的顺序，最左的是长兄，
**画法：**从左开始搜，平层为兄弟节点

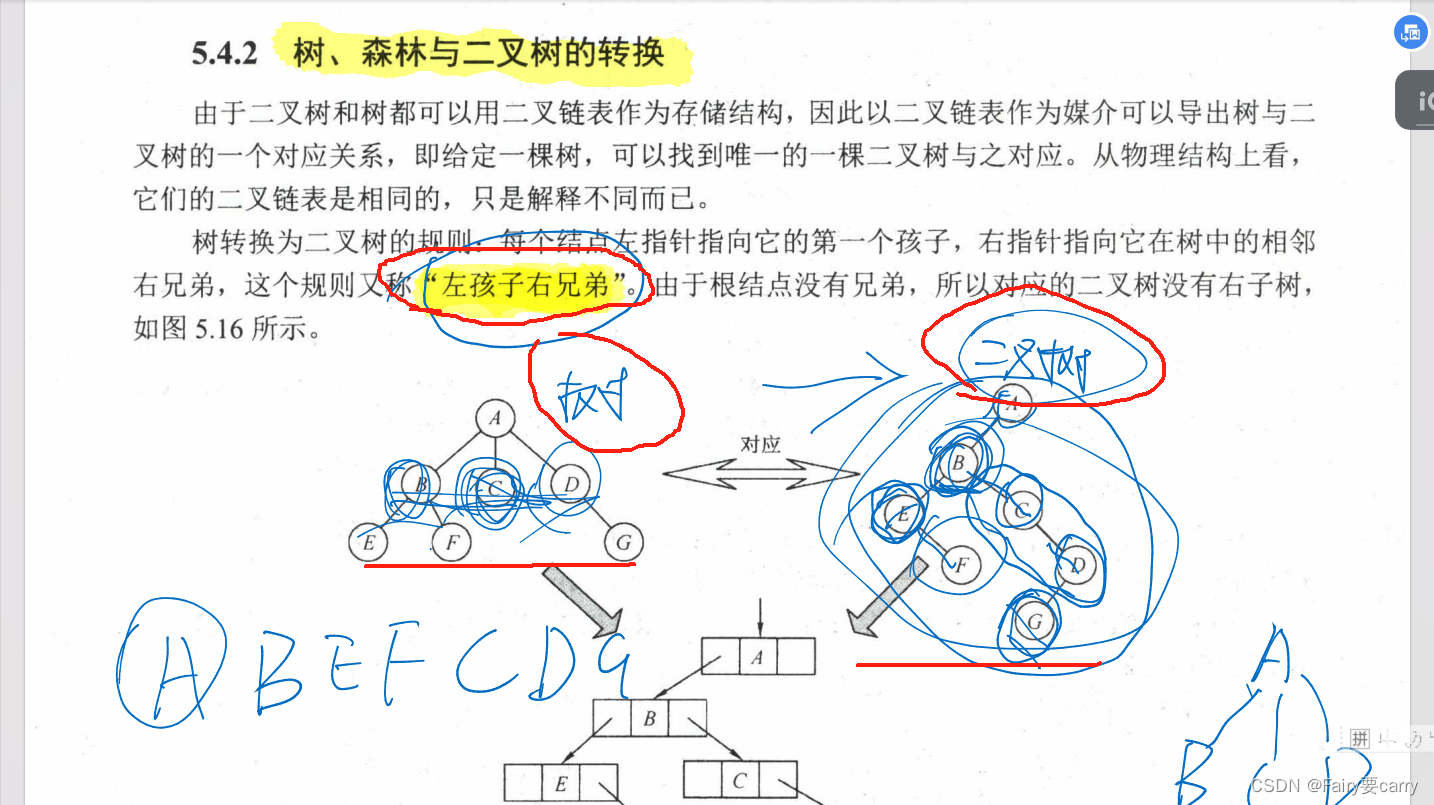
在这里插入图片描述
森林应该保持平层；注重左右带来的关系

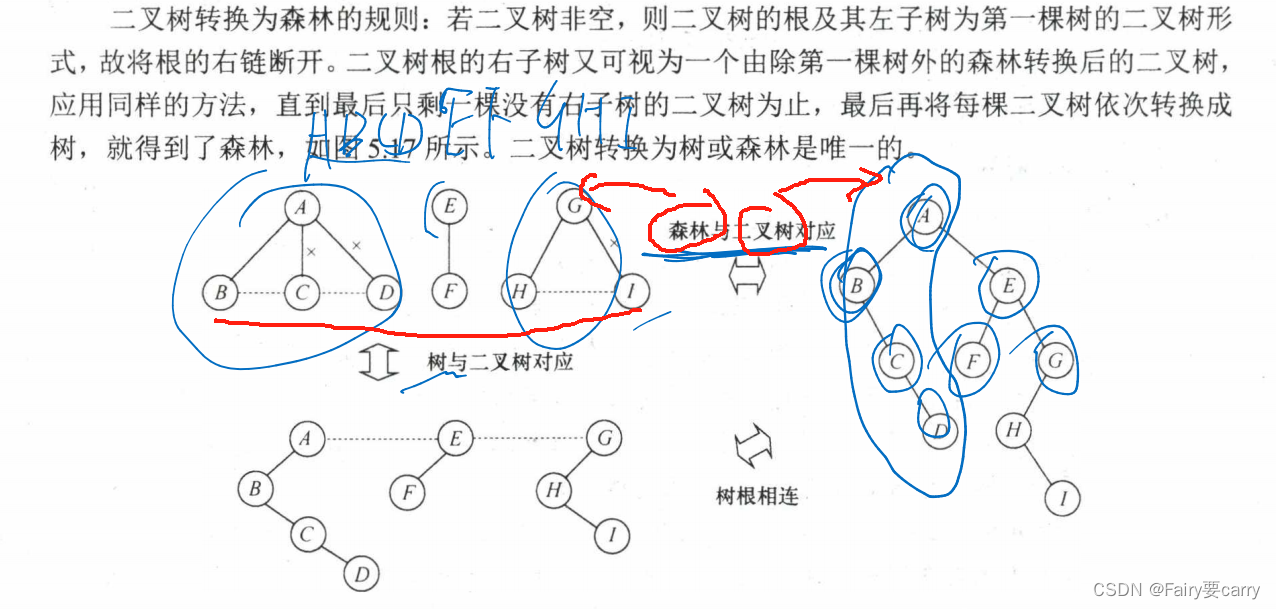
树和森林和二叉树的遍历关系：

森林和二叉树是一种遍历关系
在这里插入图片描述

9.题目

1.
在这里插入图片描述
2.
节点数=所有节点度数之和+1；

3.
最大值是高度

4.
1.节点数=至多高度+度-1
2. 度为n，第i层至多有n的i-1次方

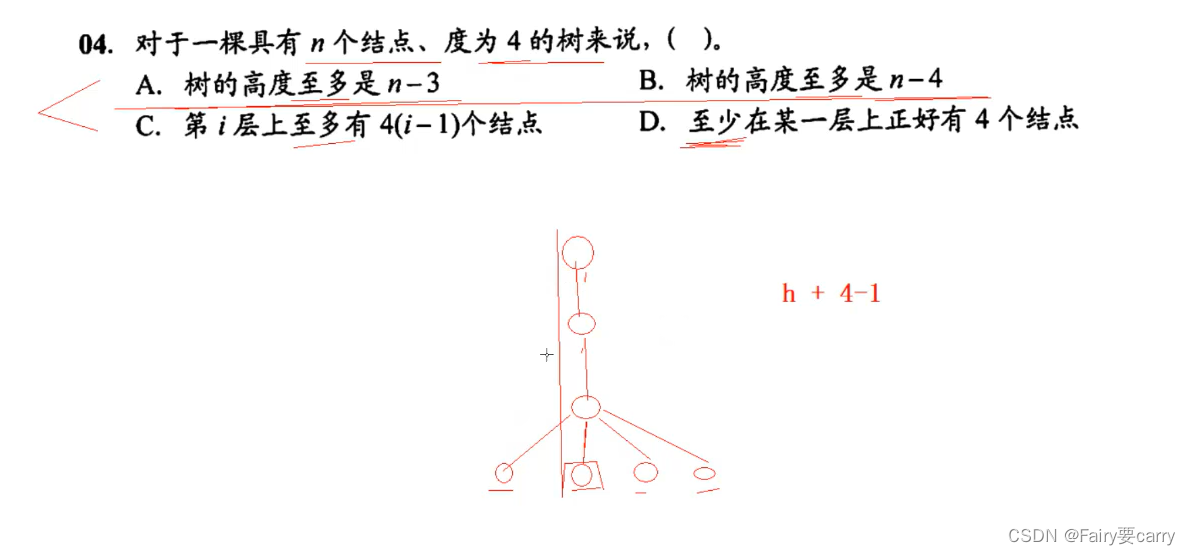
5.

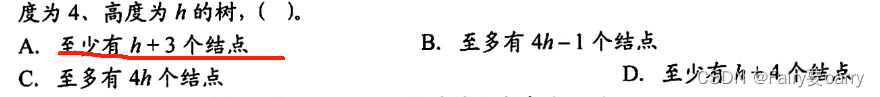
度为4，高度为h，至少节点数=h+4-1
度为4，高度为h，最多节点数：(4^h-1)/(度-1)

6
logm(n(m-1)+1)
在这里插入图片描述
7.

n节点总数=对应度数对应的节点个数+…
n0=n-n1-n2-n3-n4…
n节点总数=叶子节点个数n0+其余度数节点的累加

8.
1.完全二叉树的高度为：(log2n)+1，n为节点个数**（注意一定要是完全二叉树）**
否则链式情况需要考虑，可能有4个节点高度为4
2.如果一个完全二叉树没有左孩子，那么该节点一定是叶子节点

9.
需要注意i是否是>0，如果i从0开始，那么第i个节点的左孩子为2i+1，否则为2i

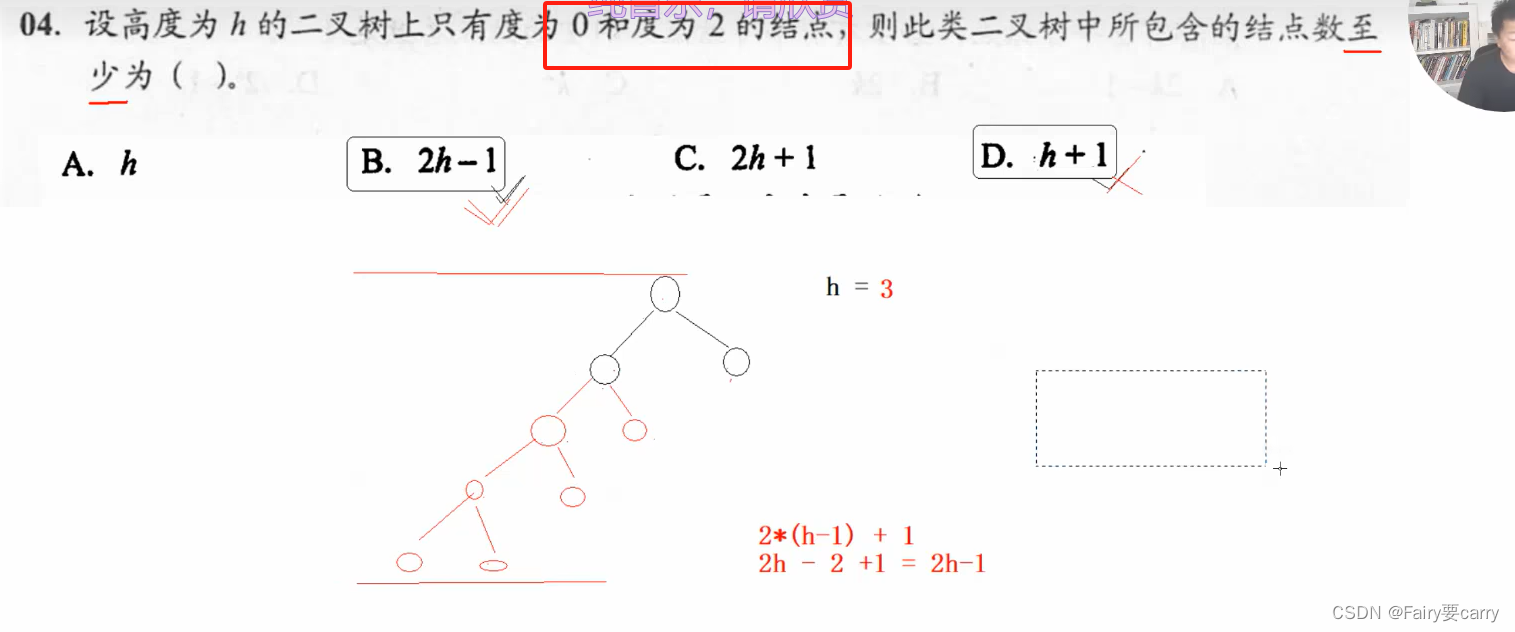
在这里插入图片描述

度为0说明该节点为叶子节点，所以在具象化的时候，我们只需要重点在度为2上，所含节点数至少为：2(h-1)+1*
高度为h，所包含节点数至少为2h-1

在这里插入图片描述
11.
最小高度，马上想到完全二叉树，完全二叉树的高度为：（log2n）+1，2为叉树，n为节点数

在这里插入图片描述

12.
公式一：节点总数2n=n0+n1+n2（各度数节点之和）
公式二：节点总数2n=非叶子节点n1数量1+n22（度数）+1

在这里插入图片描述
13.
二叉树最大深度，每层节点数最少即可，每层最少为2，所以2*h- 1=节点数n

14.

完全二叉树，已知高为h，最少节点——>(log2^n)+1=h)
由于高度h的满二叉树共有2^h-1个结点
高度为h-1的满二叉树有2^(h-1)-1个结点
可得2^(h-1)-1 < n <=2^h-1
不等式同时+1：2h-1 < n+1 <=2h
不等式同时取对数：
h-1 < log2n+1 <= h
在这里插入图片描述
15.
计算满二叉树的节点个数：2^n-1，比如这里的五层，就是2的5次方-1
如果是计算某i层的节点个数：2^(i-1)

16.
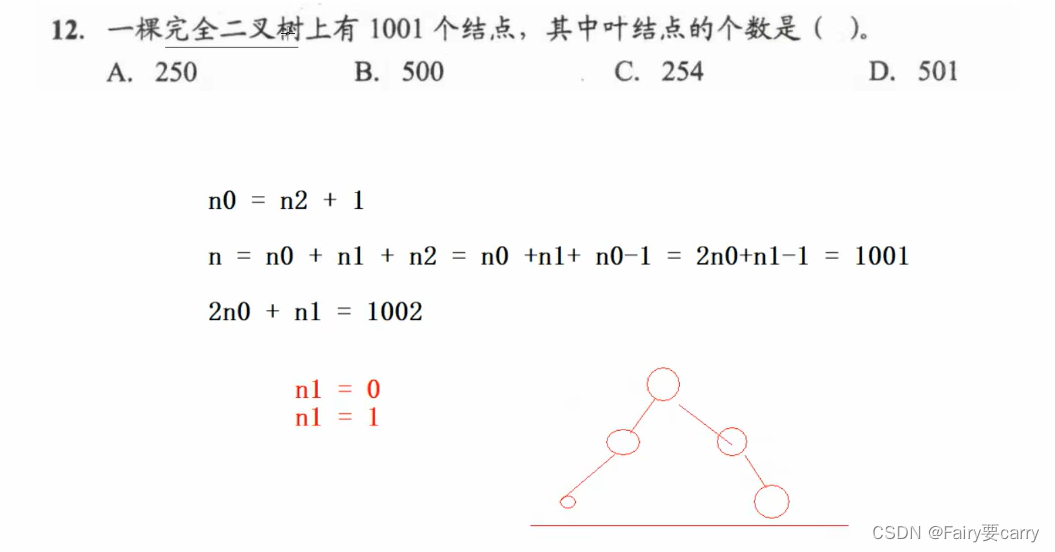
方法一：必然大于n/2，所以D
方法二：1.n0=n2+1 ；2.n=n0个数+n1+n2；3.然后完全二叉树的n1不是0就是1，再往里代入，只有D满足
在这里插入图片描述

17.
完全二叉树前n层至多节点数：2^n-1——>前6层最多有 2 ^6-1
完全二叉树前n层至少节点数：2^(n-1)
满二叉树某层节点数：2^(i-1)
满二叉树所有节点数：2^n-1
在这里插入图片描述
18.
1.124个叶子节点，说明这是n0的数量
2.n0=n2+1；n2=n0-1；
3.n=n0+n1+n2——>n=2n0+n1-1
带入n0=124,n1=0/1求解

在这里插入图片描述
19.
1.空指针数量=n+1
2.结点数=度+1

20
判断节点所在层数的公式：[log2(n)]+1，向下取整

21.
m叉树拥有n个节点，最小高度为：[logm(n(m-1))]向上取整

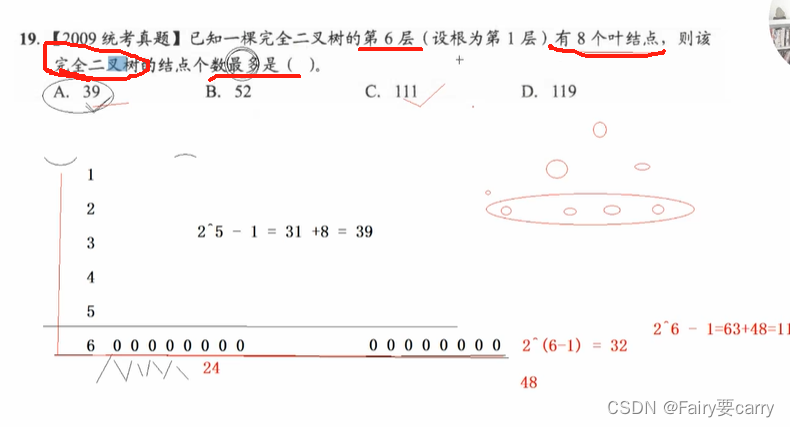
在这里插入图片描述
21.
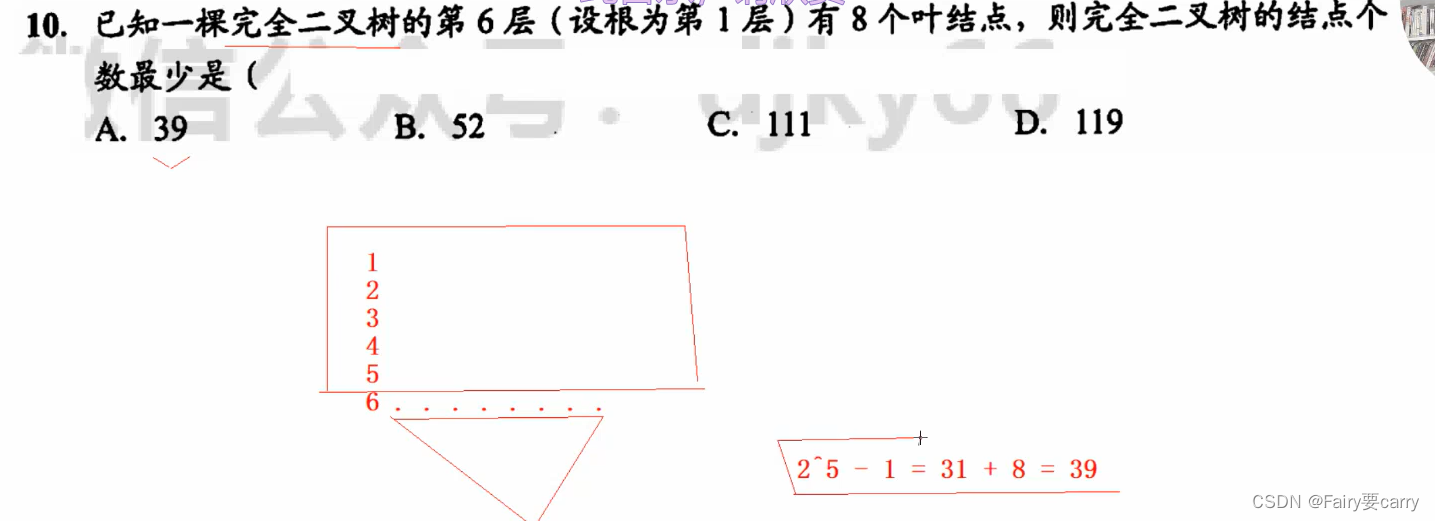
1.首先计算前5层，节点数为：2^5-1（相当于满二叉树）=31
2.第6层有8个叶子节点，有两种情况：倒数第一层或者倒数第二层，因为考虑最多节点数，所以为倒数第二层
第i层节点数为最大：2^(i-1)=32，所以第6层非叶子节点个数为32-8=24个，所以第7层有48个
3.总数为：31+32+48=111