一、工作原理
1. 正则化网络
dropout 将遍历网络的每一层,并设置消除神经网络中节点的概率。
-
1. 每个节点保留/消除的概率为0.5:
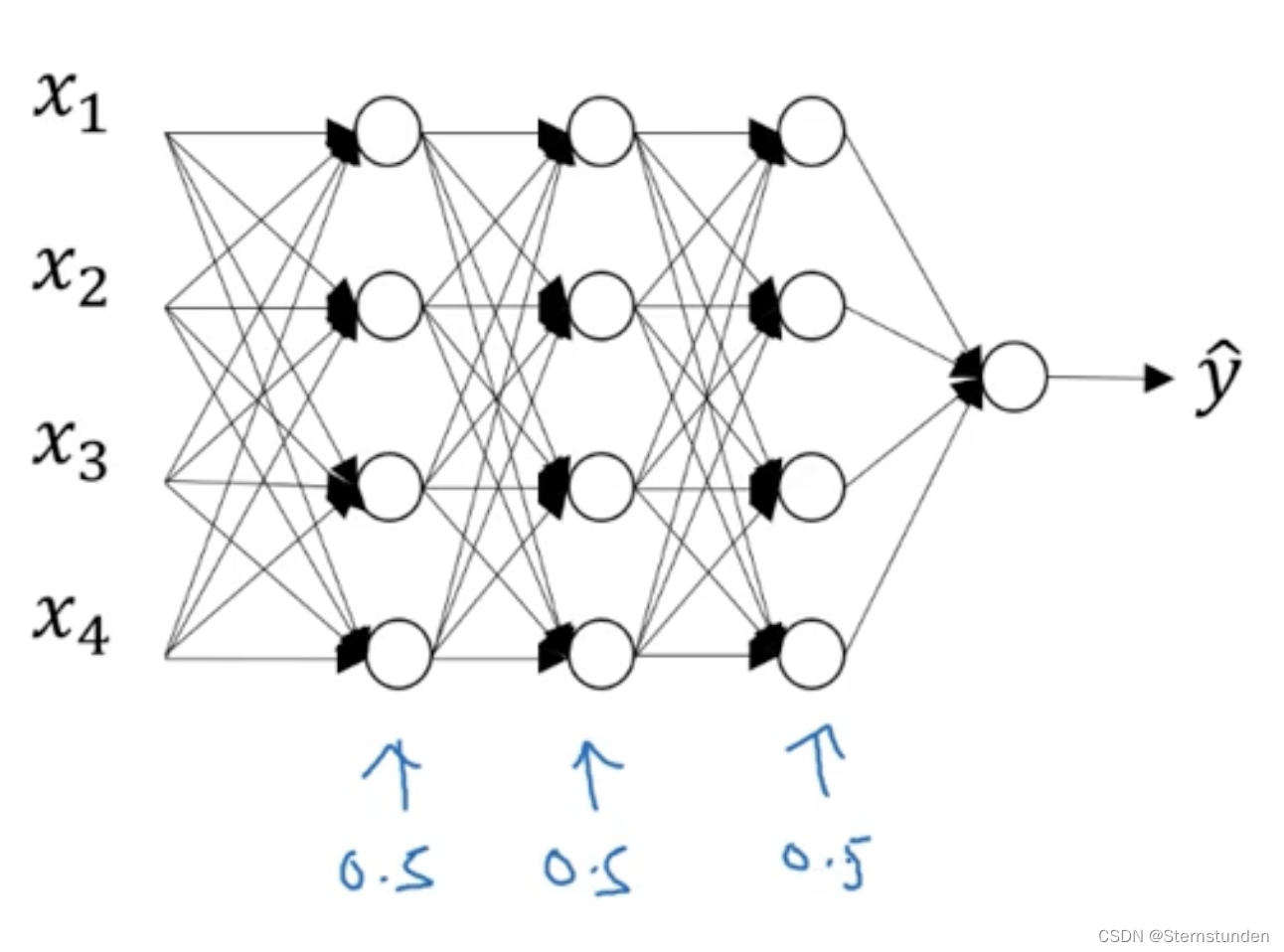
-
2. 消除节点:
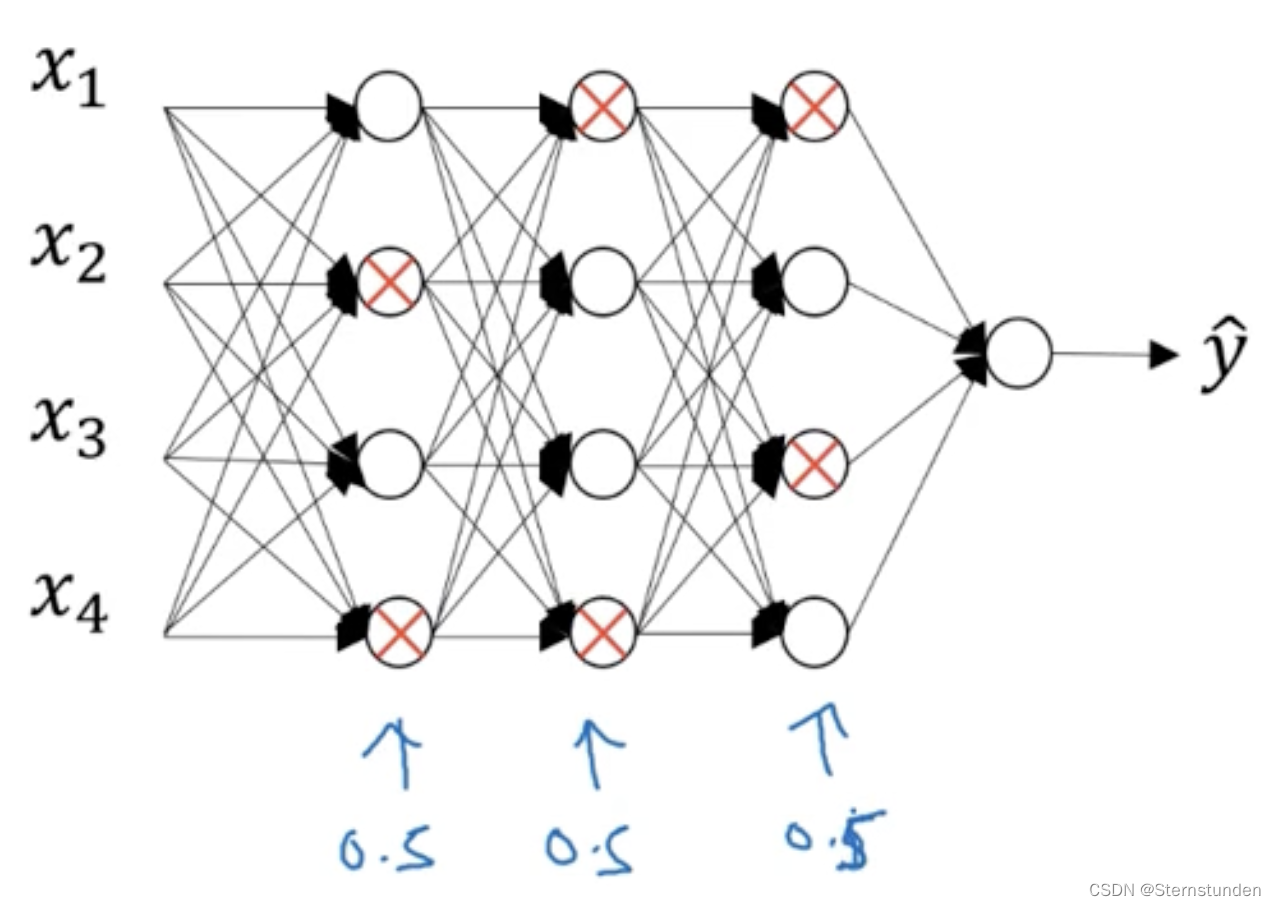
-
3. 得到一个规模更小的神经网络:

2. dropout 技术
最常用:反向随机失活 "Inverted dropout"
以三层网络 (l=3) 为例:
keep-prob = 0.8 #保留某个隐藏单元的概率 #生成随机矩阵,每个单元对应值为1的概率是0.8,用于决定第三层哪些元素应该归零 d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep-prob #元素相乘,从第三层获取激活函数,过滤d3中所有等于0的元素 a3 = np.multiply(a3,d3) a3 /= keep-prob #dropout方法:修正,使得a3期望值不变
Inverted dropout 通过除以 keep-prob,确保激活值的期望值不变,使得测试阶段更加容易。
每次梯度下降归零的隐藏单元可能不一样。
3. 在测试阶段训练算法
-
将第0层激活函数标记为测试样本x
a^{[0]} = x
-
在测试阶段不使用 dropout 技术,我们不希望输出结果随机。特别地:
z^{[1]} = w^{[1]} a^{[0]} +b^{[1]}
a^{[1]} = g^{[1]}(z^{[1]})
z^{[2]} = w^{[2]} a^{[1]} +b^{[2]}
a^{[2]} = g^{[2]}(z^{[2]})
...
\widehat{y}
目标:在测试阶段即使不执行 dropout,激活函数的预测结果也不会发生变化
二、理解 dropout
-
1. 每次 dropout 会生成一个更小的神经网络。
-
2. 收缩权重的平方范数:单元不能依赖任何特征 (该单元的任何特征都有可能被随机清除),故不会给任何一个输入加上过多的权重。
-
3. 一般来说,某层的隐藏单元越多,该层的 keep-prob 越小;可以某些层用 dropout,某些层不用。
用途:防止过拟合,常用在输入数据不足的情况 (如计算机视觉)。
缺点:代价函数 J 不再被明确定义,结果难以复查。
三、其他正则化方法
1. 增加训练集
以图片为例,可将图片进行水平翻转/旋转/裁剪/放大/扭曲图片,可扩增算法数据。(但需要人工验证图片经过处理后仍是原物)
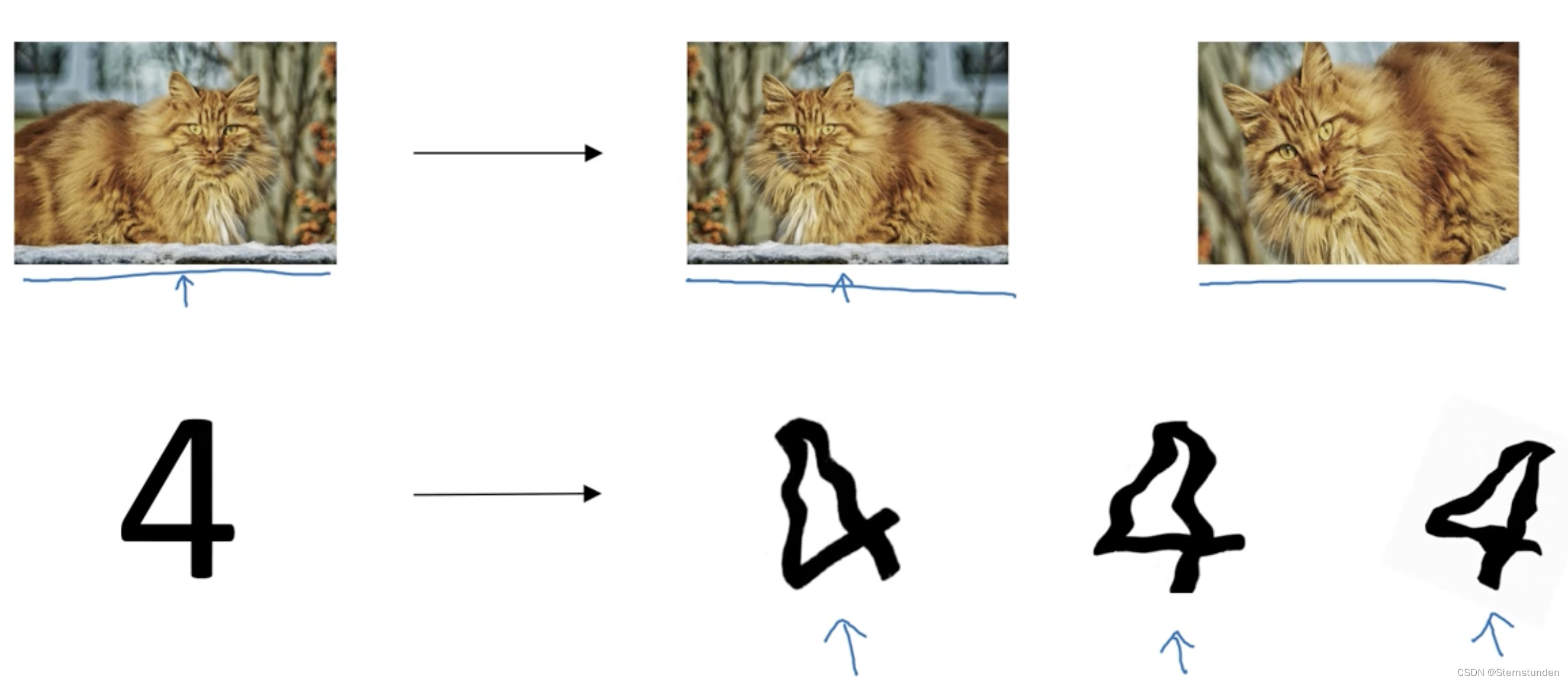
2. early stopping
运行梯度下降时,绘制训练误差或代价函数 J 的优化过程 + 验证集的误差
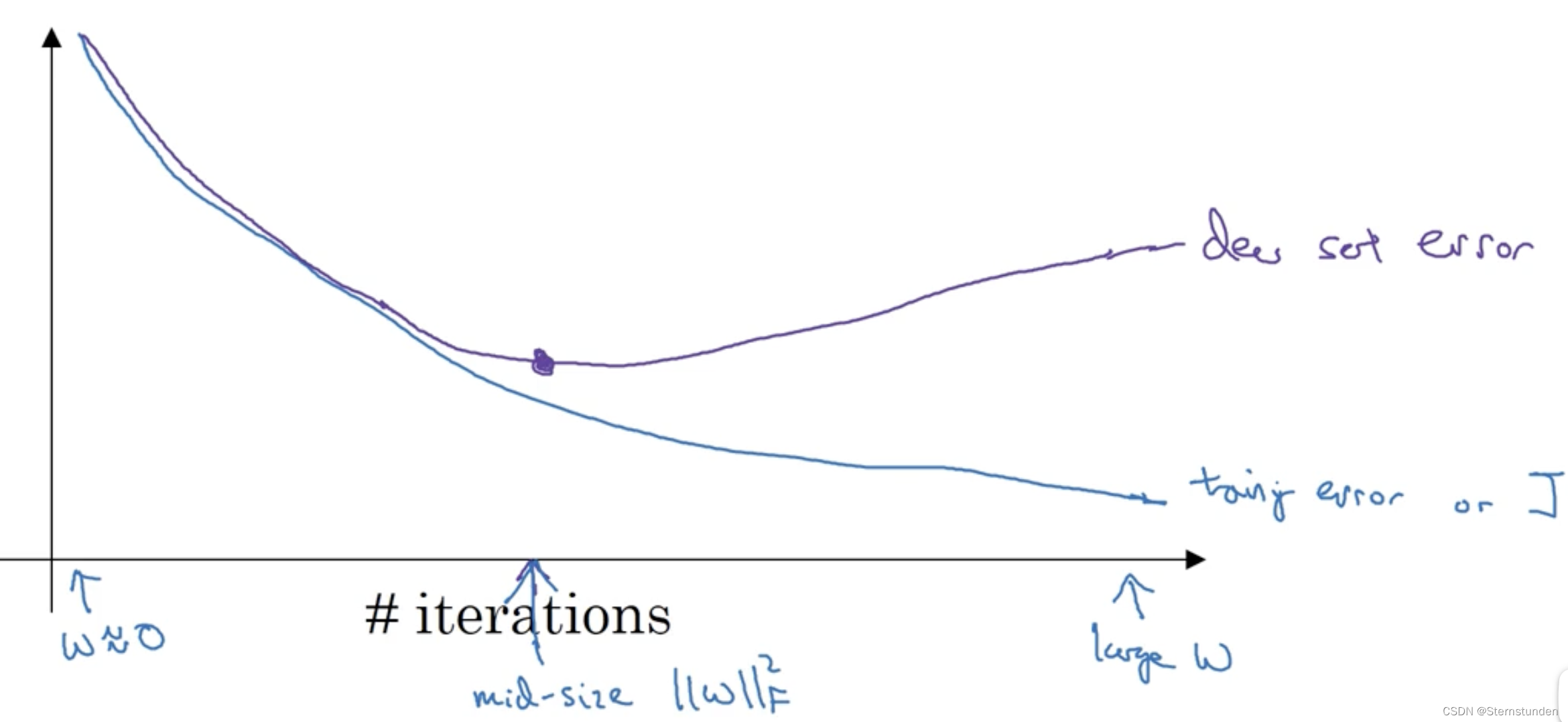
early stopping:在中间点停止迭代过程,即提早停止训练神经网络。
优点:只需要一次梯度下降,就可以找到 w 的较小值、中间值、较大值。
缺点:不能同时进行代价函数 J 的优化和 防止过拟合两个问题的解决。
3. L2 正则化
缺点:神经网络的训练时间更长,需要尝试很多次正则化参数 \lambda 的值,计算代价高。