目录
面试题 38 : 每日温度
面试题 39 : 直方图最大矩形面积
方法一、暴力求解
方法二、递归求解
方法三、单调栈法
面试题 40 : 矩阵中的最大矩形
面试题 38 : 每日温度
题目:
输入一个数组,它的每个数字是某天的温度。请计算每天需要等几天才会出现更高的温度。例如,如果输入数组 [35, 31, 33, 36, 34],那么输出为 [3, 1, 1, 0, 0]。由于第 1 天的温度是 35℃,要等 3 天才会出现更高的温度 36℃,因此对应的输出为 3。第 4 天的温度是 36℃,后面没有更高的温度,它对应的输出是 0。其他的以此类推。
分析:
解决这个问题的直观方法很多人很快就能想到。对于数组中的每个温度,可以扫描它后面的温度直到发现一个更高的温度为止。如果数组包含 n 天的温度,那么这种思路的时间复杂度是 O(n^2)。
下面通过一个具体的例子来分析这个问题的规律。假设输入的表示每天的温度的数组为 [35, 31, 33, 36, 34]。第 1 天的温度是 35℃,此时还不知道后面会不会有更高的温度,所以先将它保存到一个数据容器中。第 2 天的温度是 31℃,比第 1 天温度低,同样也保存到数据容器中。第 3 天的温度是 33℃,比第 2 天的温度高,由此可知,第 2 天需要等 1 天才有更高的温度。
每次从数组中读取某一天的温度,并且都将其与之前的温度(也就是已经保存在数据容器中的温度)相比较。从离它较近的温度开始比较看起来是一个不错的选择,也就是后存入数据容器中的温度先拿来比较,这契合 "后进先出" 的特性,所以可以考虑用栈来实现这个数据容器。同时,需要计算出现更高温度的等待天数,存入栈中的数据应该是温度在数组中的下标。等待的天数就是两个温度在数组中的下标之差。
因此,处理到第 3 天的温度时,栈的状态为 [0, 1]。在知道第 2 天需要等 1 天将出现更高的温度之后,它就没有必要再保存在栈中,将它出栈。第 3 天的温度也需要入栈,以便和以后的温度比较,此时栈的状态为 [0, 2]。
第 4 天的温度是 36℃。从栈顶开始与之前的温度比较,它比第 3 天的温度 33℃ 高,因此第 3 天需要等 1 天就会出现更高的温度,这一天在数组中的下标 2 出栈。它也比第 1 天的温度 35℃ 高,因此第 1 天需要等 3 天才会出现更高的温度,这一天在数组中的下标 0 出现。然后将第 4 天在数组中的下标 3 入栈,以便和以后的温度比较。此时栈的状态为 [3]。最后一天的温度是 34℃,比位于栈顶的第 4 天的温度低,将其入栈,最终栈的状态是 [3, 4]。最终留在栈中的两天的后面都没有出现更高的温度。
解决这个问题的思路总结起来就是用一个栈保存每天的温度在数组中的下标。每次从数组中读取一个温度,然后将其与栈中保存的温度(根据下标可以得到温度)进行比较。如果当前温度比位于栈顶的温度高,那么就能知道位于栈顶那一天需要等待几天才会出现更高的温度。然后出栈 1 次,将当前温度与下一个位于栈顶的温度进行比较。如果栈中已经没有比当前温度低的温度,则将当前温度在数组中的下标入栈。
代码实现:
class Solution {
public:vector<int> dailyTemperatures(vector<int>& temperatures) {int n = temperatures.size();vector<int> result(n, 0);stack<int> st;for (int i = 0; i < n; ++i){while (!st.empty() && temperatures[i] > temperatures[st.top()]){result[st.top()] = i - st.top();st.pop();}
st.push(i);}return result;}
};保存在栈中的温度(通过数组下标可以得到温度)是递减排序的。这是因为如果当前温度比位于栈顶的温度高,位于栈顶的温度将出栈,所以每次入栈时当前温度一定比位于栈顶的温度低或相同。
假设输入数组的长度为 n。虽然上述代码中有一个嵌套的二重循环,但它的时间复杂度是 O(n),这是因为数组中每个温度入栈、出栈各 1 次。这种解法的空间复杂度也是 O(n)。
面试题 39 : 直方图最大矩形面积
题目:
直方图是由排列在同一基线上的相邻柱子组成的图形。输入一个由非负数组成的数组,数组中的数字是直方图中柱子的高。求直方图中最大矩形面积。假设直方图中柱子的宽都为 1。例如,输入数组 [3, 2, 5, 4, 6, 1, 4, 2],其对应的直方图如下图所示,该直方图中最大矩形面积为 12,如阴影部分所示。

分析:
矩形的面积等于宽乘以高,因此只要能确定每个矩形的宽和高,就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始,到下标为 j 的柱子结束,那么这两根柱子之间的矩形(含两端的柱子)的宽是 j - i + 1。矩形的高就是两根柱子之间的所有柱子最矮的高度。例如,上图中从下标为 2 的柱子到下标为 4 的柱子之间的矩形宽度是 3,矩形的高度最多只能是 4,即它们之间 3 根柱子最矮的高度。
方法一、暴力求解
如果能逐一找出直方图中所有的矩形并比较它们的面积,就能得到最大矩形面积。下面使用嵌套的二重循环遍历所有矩形,并比较它们的面积。
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int maxArea = 0;for (int i = 0; i < heights.size(); ++i){int minHeight = heights[i];for (int j = i; j < heights.size(); ++j){if (heights[j] < minHeight)minHeight = heights[j];int area = minHeight * (j - i + 1);
if (area > maxArea)maxArea = area;}}return maxArea;}
};这种解法的时间复杂度是 O(n^2),空间复杂度是 O(1)。
方法二、递归求解
上图的直方图中最矮的柱子在数组中的下标是 5,它的高度是 1。这个直方图的最大矩形有以下 3 种可能:
-
第 1 种是矩形通过这根最矮的柱子。通过最矮的柱子的最大矩形的高度是 1,宽度是 7。
-
第 2 种是矩形的起始柱子和终止柱子都在最矮的柱子的左侧,也就是从下标为 0 的柱子到下标为 4 的柱子的直方图的最大矩形。
-
第 3 种是矩形的起始柱子和终止柱子都在最矮的柱子的右侧,也就是从下标为 6 的柱子到下标为 7 的柱子的直方图的最大矩形。
第 2 种和第 3 种本质上来说和求整个直方图的最大矩形面积是同一个问题,可以调用递归函数解决。
class Solution {
private:int _largestRectangleArea(vector<int>& heights, int left, int right){if (left > right)return 0;if (left == right)return heights[left];
int minHeightIndex = left;for (int i = left + 1; i <= right; ++i){if (heights[i] < heights[minHeightIndex])minHeightIndex = i;}int maxArea = heights[minHeightIndex] * (right - left + 1);int area1 = _largestRectangleArea(heights, left, minHeightIndex - 1);int area2 = _largestRectangleArea(heights, minHeightIndex + 1, right);if (area1 > maxArea)maxArea = area1;if (area2 > maxArea)maxArea = area2;return maxArea;}
public:int largestRectangleArea(vector<int>& heights) {return _largestRectangleArea(heights, 0, heights.size() - 1);}
};假设输入数组的长度为 n。如果每次都能将 n 根柱子分成两根柱子数量为 n / 2 的子直方图,那么递归调用的深度为 O(logn),整个递归算法的时间复杂度是 O(nlogn)。但如果直方图中柱子的高度是排序的(递增排序或递减排序),那么每次最矮的柱子都位于直方图的一侧,递归调用的深度就是 O(n),此时递归算法的时间复杂度也变成 O(n^2)。
递归算法的空间复杂度取决于调用栈的深度,因此平均空间复杂度是 O(logn),最坏情况下的空间复杂度是 O(n)。
方法三、单调栈法
计算以每根柱子为顶的最大矩形面积,比较这些矩形面积就能得到直方图中的最大矩形面积。
以某根柱子为顶的最大矩形,一定是从该柱子向两侧延伸直到遇到比它矮的柱子,这个最大矩形的高就是该柱子的高,最大矩形的宽是两侧比它矮的柱子中间的间隔。例如,为了求上图所示的直方图中以下标为 3 的柱子为顶的最大矩形面积,应该从该柱子开始向两侧延伸,左侧比它矮的柱子的下标是 1,右侧比它矮的柱子的下标是 5。因此,以下标为 3 的柱子为顶的最大矩形的高为 4,宽为 3(左右两侧比它矮的柱子的下标之差再减 1,即 5 - 1 - 1)。
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n = heights.size();vector<int> left(n, -1);vector<int> right(n, n);
stack<int> st;for (int i = n - 1; i >= 0; --i){while (!st.empty() && heights[i] < heights[st.top()]){left[st.top()] = i;st.pop();}st.push(i);}st = stack<int>();for (int i = 0; i < n; ++i){while (!st.empty() && heights[i] < heights[st.top()]){right[st.top()] = i;st.pop();}st.push(i);}
int maxArea = 0;for (int i = 0; i < n; ++i){int area = heights[i] * (right[i] - left[i] - 1);if (area > maxArea)maxArea = area;}return maxArea;}
};这种解法的时间复杂度是 O(n),空间复杂度也是 O(n)。
面试题 40 : 矩阵中的最大矩形
题目:
请在一个由 0、1 组成的矩阵中找出最大的只包含 1 的矩形并输出它的面积。例如,在下图的矩阵中,最大的只包含 1 的矩形如阴影部分所示,它的面积是 6。

分析:
面试题 2.4 是关于最大矩形的,这个题目还是关于最大矩形的,它们之间有没有某种联系?如果能从矩阵中找出直方图,那么就能通过计算直方图中的最大矩形面积来计算矩阵中的最大矩形面积。
直方图是由排列在同一基线上的相邻柱子组成的图形。由于题目要求矩形中只包含数字 1,因此将矩阵中上下相邻的值为 1 的格子看成直方图中的柱子。如果分别以上图中的矩阵的每行为基线,就可以得到 4 个由数字 1 的格子组成的直方图,如下图所示。
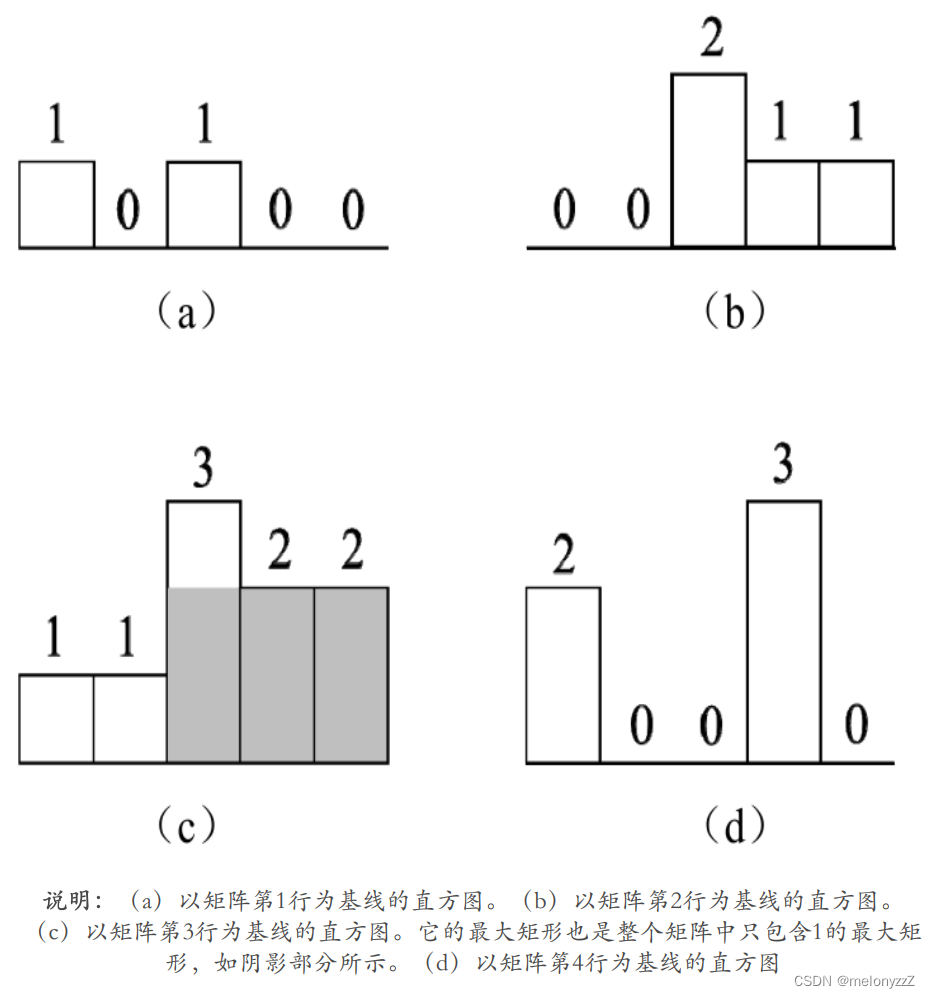
在将矩阵转换成多个直方图之后,就可以计算并比较每个直方图的最大矩形面积,所有直方图中的最大矩形就是整个矩阵中的最大矩形。
代码实现:
class Solution {
private:int largestRectangleArea(vector<int>& heights) {int n = heights.size();vector<int> left(n, -1);vector<int> right(n, n);
stack<int> st;for (int i = n - 1; i >= 0; --i){while (!st.empty() && heights[i] < heights[st.top()]){left[st.top()] = i;st.pop();}st.push(i);}st = stack<int>();for (int i = 0; i < n; ++i){while (!st.empty() && heights[i] < heights[st.top()]){right[st.top()] = i;st.pop();}st.push(i);}
int maxArea = 0;for (int i = 0; i < n; ++i){int area = heights[i] * (right[i] - left[i] - 1);if (area > maxArea)maxArea = area;}return maxArea;}public:int maximalRectangle(vector<string>& matrix) {if (matrix.size() == 0 || matrix[0].size() == 0)return 0;
int result = 0;vector<int> heights(matrix[0].size(), 0);for (int i = 0; i < matrix.size(); ++i){for (int j = 0; j < matrix[i].size(); ++j){if (matrix[i][j] == '0')heights[j] = 0;else++heights[j];}
int maxArea = largestRectangleArea(heights);if (maxArea > result)result = maxArea;}return result;}
};