一、说明

   Geometry_tools 是一个 Python 包，旨在帮助您处理和可视化双曲空间和射影空间上的群动作。

   该包主要构建在 numpy、matplotlib 和 scipy 之上。或者，该包可以使用 Sage 提供的工具来执行（缓慢的）精确计算。

   几何工具可以帮助您：

• 在多个模型（即克莱因模型、双曲面模型、射影模型、庞加莱模型和半空间模型）中对双曲空间中的对象执行数值（或有时是精确）计算

• 在双曲平面、实射影平面、复射影线上画出漂亮的图画

• 将有限生成组的表示处理为$\text{O}(d,1)$
  ,$\text{GL}(d,\mathbb{R})$， 和$\text{GL}(d,\mathbb{C})$

• 使用 Coxeter 群的表示进行实际计算$\text{GL}(d,\mathbb{R})$

• 使用有限状态自动机在字双曲群中进行一些简单的计算在双曲平面、实射影平面、复射影线上画出漂亮的图画

   还提供了对 3D 图形的一些有限支持（通过 matplotlib）。

   这个包的所有功能（在数学上）都不是很深。大多数情况下，该软件包只是包装了更复杂的工具，旨在使您可以轻松地快速绘制好图画。在,${\mathbb{H}}^2$，和${\mathbb{H}}^3$ 和$\mathbb{R}{P}^2$ 和$\mathbb{C}{P}^1$。

二、​环境问题：如何安装

   现在，最简单的安装方法是从 git 存储库下载或克隆geometry_tools项目，然后运行

pip install .

   从您下载它的目录中。如果您没有安装 pip，则应先安装 pip。或者，您可以尝试从项目目录运行（不建议这样做）。

python setup.py install

三、实现一个简单的例子

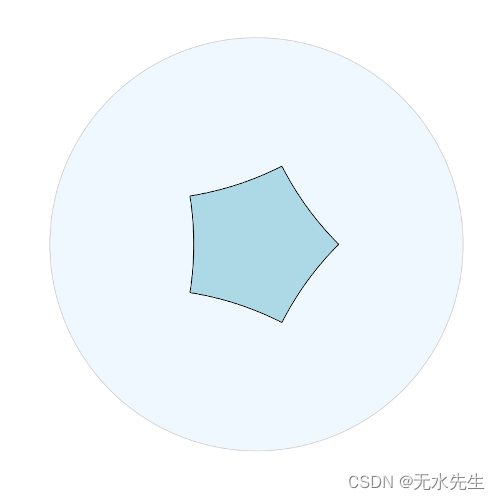
   要在双曲平面上绘制直角五边形的图片：

from geometry_tools import hyperbolic, drawtools
from numpy import pi# make a right-angled pentagon
pentagon = hyperbolic.Polygon.regular_polygon(5, angle=pi/2)# draw the pentagon
figure = drawtools.HyperbolicDrawing()
figure.draw_plane()
figure.draw_polygon(pentagon, facecolor="lightblue")figure.show()

   代码结果：

​

四、绘制双曲组

   该软件包方便绘制平铺图片geometry_tools在${\mathbb{H}}^2$空间.在这里，我们将可视化 （2,3,7） 三角形平铺：

from geometry_tools import hyperbolic, coxeter, drawtools
from geometry_tools.automata import fsa# make the triangle group representation and load a finite-state automaton
triangle_group = coxeter.TriangleGroup((2,3,7))
triangle_rep = triangle_group.hyperbolic_rep()
triangle_fsa = triangle_group.automaton()# find a fundamental domain for the action by finding 
# fixed points of length-2 elements
vertices = triangle_rep.isometries(["ab", "bc", "ca"]).fixed_point()
fund_triangle = hyperbolic.Polygon(vertices)# find all orientation-preserving isometries of length at most 30
words = triangle_fsa.enumerate_words(30)
even_words = [word for word in words if len(word) % 2 == 0]
pos_isometries = triangle_rep.isometries(even_words)# draw the translated triangles
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(pos_isometries @ fund_triangle, facecolor="royalblue", edgecolor="none")fig.show()

​
   首先，首先实例化该类coxeter.TriangleGroup以获得一个 （2,3,7） 三角形组，并将其几何表示计算为双曲平面的等距：

# get a representation for a triangle group.
# (these are built in to the program)
from geometry_tools import hyperbolic, coxeter, drawtoolstriangle_rep = coxeter.TriangleGroup((2,3,7)).hyperbolic_rep()

​
   我们可以使用子包绘制组的反射墙：geometry_tools.drawtools

# find the fixed points at infinity for the generating reflectionsreflections = triangle_rep.isometries(["a", "b", "c"])
walls = hyperbolic.Geodesic.from_reflection(reflections)wall_a, wall_b, wall_c = wallsfig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()fig.draw_geodesic(wall_a, color="green")
fig.draw_geodesic(wall_b, color="blue")
fig.draw_geodesic(wall_c, color="red")

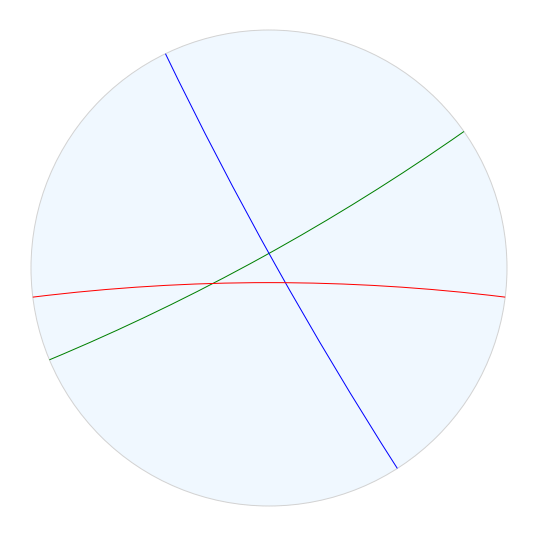
   我们可以通过取三角形群的顶点是群的长度 2 元素的固定点的三角形来找到三角形群的基本域。

triangle_vertices = triangle_rep.isometries(["ab", "bc", "ac"]).fixed_point()
fund_triangle = hyperbolic.Polygon(triangle_vertices)
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(fund_triangle, facecolor="lightgreen")

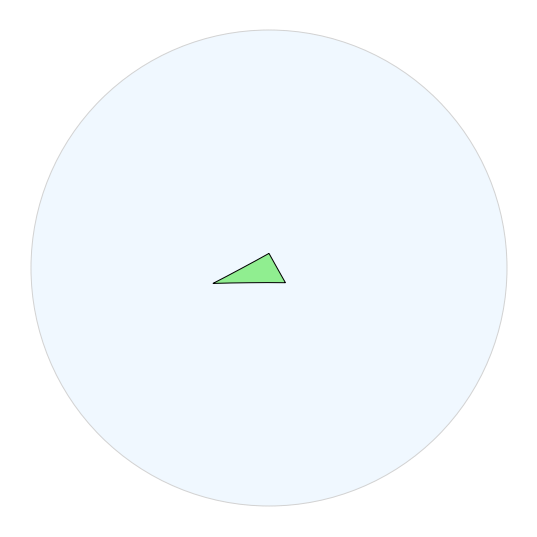
   如果我们想开始可视化$({\mathbb{H}}^2)$我们从这个三角形组中得到，我们可以开始绘制这个基本域的翻译。要做到这一点，最简单（但效率较低且吸引人）的方法是，只绘制由组中自由简化的单词图像翻译的基本域的副本。

words = triangle_rep.free_words_less_than(5)
isometries = triangle_rep.isometries(words)tiles = isometries @ fund_trianglefig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()fig.draw_polygon(tiles, facecolor="lightgreen")

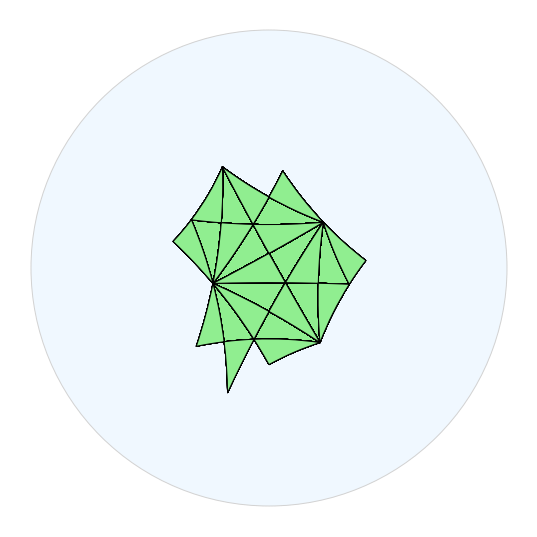
五、使用有限状态自动机加快速度

   绘制由所有自由缩小的单词的图像翻译的三角形的副本有点慢。而且，我们最终多次在其顶部绘制同一个三角形。我们可以使用有限状态自动机为组中的每个元素选择一个唯一的单词，从而加快该过程。

   Geometry_tools.automata 子包提供了一些用于处理有限状态自动机的工具。它可以加载和操作 kbmag 程序生成的自动机。虽然 kbmag 不包含在 Geometry_tools 中，但该包确实为许多单词双曲群提供了预先计算的自动机。要获取预先计算的自动机列表，请导入 automata.fsa 子模块并调用 fsa.list_builtins()。调用 fsa.load_builtin() 加载自动机。

   感谢 Florian Stecker 提供的代码，geometry_tools 包还可以为任何 Coxeter 组生成自动机。所以我们可以得到 (2,3,7) 三角形组的自动机，如下所示：

# construct the (2,3,7) automaton
triangle_fsa = coxeter.TriangleGroup((2,3,7)).automaton()# get a unique word for each group element of length < 25.
# (we convert to a list since enumerate_words returns a generator)
words = list(triangle_fsa.enumerate_words(30))free_words = list(triangle_rep.free_words_less_than(9))# compare unique words of length <30 to freely reduced words of length <9.
# when we don't consider the relation, we get many redundant words!
len(words), len(free_words)

(5951, 585937)
   为了让图片更漂亮一点，我们可以制作一个只接受偶数长度的单词的自动机。然后我们可以得到所有等距的集合，这些等距是这个自动机接受的单词的图像。

even_triangle_fsa = triangle_fsa.even_automaton()
pos_isometries = triangle_rep.automaton_accepted(even_triangle_fsa, 15)tiles = pos_isometries @ fund_trianglefig = drawtools.HyperbolicDrawing()
fig.draw_plane()
fig.draw_polygon(tiles, facecolor="royalblue", edgecolor="none")

回顾一下，以下是生成上图所需的所有代码：

from geometry_tools import hyperbolic, coxeter, drawtools# make the triangle group representation
triangle_group = coxeter.TriangleGroup((2,3,7))
triangle_rep = triangle_group.hyperbolic_rep()# find a fundamental domain for the action by finding 
# fixed points of length-2 elements
vertices = triangle_rep.isometries(["ab", "bc", "ca"]).fixed_point()
fund_triangle = hyperbolic.Polygon(vertices)# find all orientation-preserving isometries of length at most 30 using an automaton
triangle_fsa = triangle_group.automaton(even_length=True)
pos_isometries = triangle_rep.automaton_accepted(triangle_fsa, 15)# draw the translated triangles
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(pos_isometries @ fund_triangle, facecolor="royalblue", edgecolor="none")

六、资源和代码

本文资源下载地址是：
vvvvvv

(未完待续)