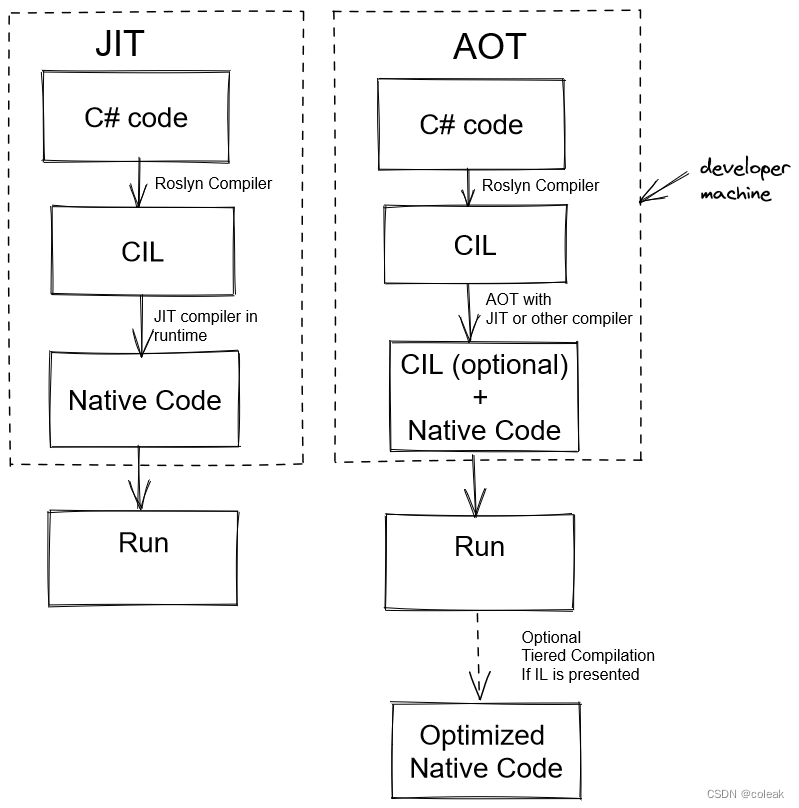
题目链接:LCR 037. 行星碰撞 - 力扣(LeetCode)
题目:
输入一个表示小行星的数组,数组中每个数字的绝对值表示小行星的大小,数字的正负号表示小行星运动的方向,正号表示向右飞行,负号表示向左飞行。如果两颗小行星相撞,那么体积较小的小行星将会爆炸最终消失,体积较大的小行星不受影响。如果相撞的两颗小行星大小相同,那么它们都会爆炸消失。飞行方向相同的小行星永远不会相撞(因为每一颗小行星以相同的速度移动)。求最终剩下的小行星。例如,有 6 颗小行星 [4, 5, -6, 4, 8, -5],如下图所示(箭头表示飞行的方向),它们相撞之后最终剩下 3 颗小行星 [-6, 4, 8]。
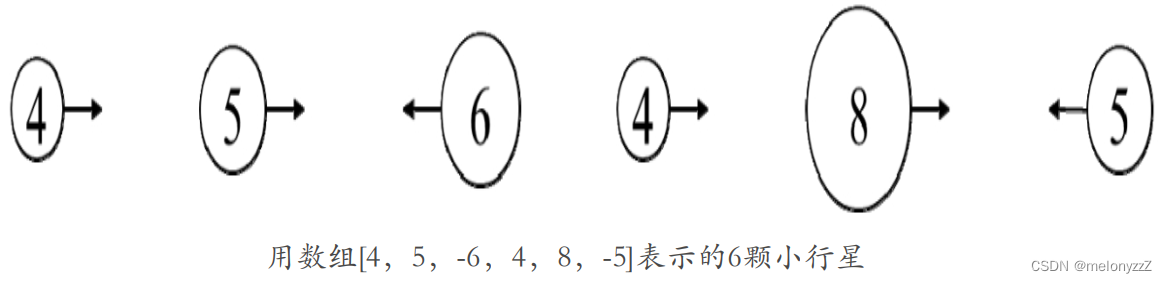
分析:
下面以一个具体的例子来分析小行星碰撞的规律。先假设有 6 颗小行星 [4, 5, -6, 4, 8, -5],然后逐一分析它们的飞行情况。第 1 颗是向右飞行的大小为 4 的小行星,此时还不知道它会不会和其他小行星碰撞,可以先将它保存到某个数据容器中。第 2 颗还是一颗向右飞行的小行星,它的大小为 5,它和前面一颗小行星的飞行方向相同,所以不会碰撞。但现在还不知道它会不会和后面的小行星碰撞,因此也将它保存到数据容器中。第 3 颗是一颗向左飞行的小行星,大小为 6,由于它和前面两颗小行星是相向而行的,因此会和前面两颗小行星相撞。先后向数据容器中保存了大小为 4、5 的两颗小行星,后保存到数据容器中的小行星先和其他的小行星相撞,这符合 "后进先出" 的顺序,所以可以考虑用栈来实现这个数据容器。
根据题目的碰撞规则,小的小行星将会爆炸消失,因此当大小分别为 5 和 6 的两颗小行星相撞时,大小为 5 的小行星会爆炸消失。大小为 6 的小行星继续向左飞行,它将和大小为 4 的小行星相撞。大小为 4 的小行星爆炸消失,留下大小为 6 的小行星向左飞行。此时左边已经没有更多的小行星和这颗大小为 6 的小行星相撞,将它入栈。
接下来是两颗向右飞行的小行星,大小分别为 4 和 8,它们和大小为 6 的小行星背向飞行,肯定不会相撞,因此将它们也先后入栈。最后是一颗大小为 5 向左飞行的小行星,此时栈中保存了 3 颗小行星 [-6, 4, 8],大小为 8 的小行星离它最近而且相向飞行,因此它将与大小为 8 的小行星相撞,然后爆炸消失。最终剩下 3 颗小行星 [-6, 4, 8]。
上述分析过程可以用下表来总结:
| 步骤 | 小行星 | 操作 | 栈 | 注释 |
|---|---|---|---|---|
| 1 | 4 | 入栈 | [4] | |
| 2 | 5 | 入栈 | [4, 5] | |
| 3 | -6 | 相撞 | [-6] | -6、5 相撞,5 出栈;-6、4 相撞,4 出栈;-6 入栈 |
| 4 | 4 | 入栈 | [-6, 4] | |
| 5 | 8 | 入栈 | [-6, 4, 8] | |
| 6 | -5 | 相撞 | [-6, 4, 8] | -5、8 相撞 |
由此可以总结出小行星相撞的规律:
-
如果一颗小行星向右飞行,那么它一定不会和前面的小行星相撞,可以直接将它入栈。
-
如果一颗小行星向左飞行,而位于栈顶的小行星向右飞行,那么它将与位于栈顶的小行星相撞。如果位于栈顶的小行星较小,那么它将爆炸消失,也就是说它将出栈。然后判断它是否将与下一颗位于栈顶的小行星相撞。如果小行星与栈中所有小行星相撞之后仍然没有爆炸消失,那么它将入栈。
代码实现:
class Solution {
public:vector<int> asteroidCollision(vector<int>& asteroids) {vector<int> result; // 用数组模拟栈for (int as : asteroids){if (as > 0){result.push_back(as);}else // as < 0{while (!result.empty() && result.back() > 0 && result.back() < -as){result.pop_back();}if (!result.empty() && result.back() == -as){result.pop_back();}else if (result.empty() || result.back() < 0){result.push_back(as);}}}return result;}
};栈中保存的小行星彼此都不会相撞。如果栈中既有向左飞行的小行星也有向右飞行的小行星,那么所有向左飞行的小行星都位于向右飞行的小行星的左边,也就是说,栈中所有负数都位于正数的左边。