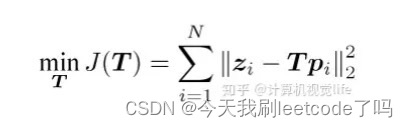图片来源
一、说明
深度学习通常被认为是人工智能的巅峰之作,它的成功很大程度上归功于数学,尤其是线性代数和微积分。本文将探讨深度学习与数学之间的深刻联系,阐明为什么数学概念是该领域的核心。
二、数学框架
从本质上讲,深度学习就是从数据中学习复杂的模式和表示。这些模式是使用数学运算捕获和操作的。以下是对所涉及的数学的仔细研究:
2.1. 线性代数
矩阵运算:神经网络被构造为相互连接的神经元层。这些连接可以表示为权重矩阵中的权重。整个前向和后向传播过程对于训练神经网络至关重要,本质上是乘法、加法和减法等矩阵运算。
激活功能:虽然线性变换是基础,但深度学习模型也采用激活函数,如 sigmoid、ReLU 或 tanh。这些函数将非线性引入网络,使其能够对数据中复杂的非线性模式进行建模。
2.2. 微积分
梯度下降:优化是训练深度神经网络的核心。微积分,尤其是梯度下降,在最小化损失函数方面起着关键作用。梯度表示损失相对于网络权重的变化率,引导权重更新朝着正确的方向发展。
链式法则:微积分中的链式规则广泛用于反向传播,这是计算网络中所有权重梯度的过程。它确保错误正确地归因于单个神经元。
三、神经网络的构建块
3.1向量和张量
数据表示:深度学习中的数据通常表示为向量或更高维的张量。例如,图像表示为多维数组,其中每个元素对应于一个像素值。
型号参数:神经网络权重和偏差也表示为张量,从而可以执行高效的并行计算。
3.2 激活函数
激活函数是代数映射,其目的是将线性映射抑制下来,导致非线性性。
3.3 代价函数
是可以控制方程精度的的函数,该函数具有凸性,也就是极值唯一性。
四、深度学习中的高等数学
4.1 概率与统计
贝叶斯深度学习:概率模型和贝叶斯推理用于深度学习中的不确定性估计,这在自动驾驶汽车和医疗诊断等应用中至关重要。
生成模型:变分自动编码器 (VAE) 和生成对抗网络 (GAN) 等高级概率模型用于生成数据、图像合成和风格迁移
4.2. 信息论
熵和交叉熵:信息论概念,如熵和交叉熵,是深度学习中使用的损失函数的核心。它们量化了信息内容和概率分布之间的差异。
4.3 图论
图神经网络:在涉及社交网络或分子等结构化数据的应用中,图神经网络利用图论原理来执行节点分类和链接预测等任务。
强化学习:强化学习算法通常涉及马尔可夫决策过程和动态规划,借鉴数学优化和控制理论。
五、结论
深度学习与数学的深刻联系凸显了其在建模数据中复杂关系方面的卓越能力。
理解深度学习的数学基础不仅仅是一项理论练习,而是研究人员、工程师和数据科学家推动人工智能界限的实际需要。
简单示例:
它通过使用 NumPy 在 Python 中实现的简单前馈神经网络,演示了线性代数和微积分在深度学习中的使用:
import numpy as np# Define a simple feedforward neural network
class NeuralNetwork:def __init__(self, input_size, hidden_size, output_size):self.input_size = input_sizeself.hidden_size = hidden_sizeself.output_size = output_size# Initialize weights and biases with random valuesself.weights_input_hidden = np.random.randn(self.input_size, self.hidden_size)self.biases_hidden = np.zeros((1, self.hidden_size))self.weights_hidden_output = np.random.randn(self.hidden_size, self.output_size)self.biases_output = np.zeros((1, self.output_size))def forward(self, inputs):# Linear transformation and activation in the hidden layerhidden_input = np.dot(inputs, self.weights_input_hidden) + self.biases_hiddenhidden_output = 1 / (1 + np.exp(-hidden_input)) # Sigmoid activation function# Linear transformation in the output layeroutput_input = np.dot(hidden_output, self.weights_hidden_output) + self.biases_outputpredicted_output = 1 / (1 + np.exp(-output_input)) # Sigmoid activation functionreturn predicted_output# Create a sample input
input_data = np.array([[0, 1]])# Initialize the neural network with 2 input neurons, 2 hidden neurons, and 1 output neuron
neural_network = NeuralNetwork(input_size=2, hidden_size=2, output_size=1)# Perform a forward pass to get predictions
predictions = neural_network.forward(input_data)# Display the predictions
print("Predicted Output:", predictions)在此代码片段中,我们使用 Python 和 NumPy 创建一个简单的前馈神经网络。它重点介绍了矩阵乘法、sigmoid 激活函数(微积分概念)和矢量化运算的使用——这些深度学习的关键组成部分依赖于线性代数和微积分。神经网络的前向传递展示了这些数学概念的实际应用,展示了它们与深度学习密不可分的联系。