前言
- 这两天机器狗终于搞定了,一个控制ROS大佬,一个计院编程大佬,竟然真把创新点这个弄出来了,牛牛牛牛(菜鸡我只能负责在旁边喊加油)。下午翘了自辩课来刷题,这次应该是元旦前最后一刷了,下午尽量刷多点吧(活就是2024再说嘿嘿)~
96. 不同的二叉搜索树 - 力扣(LeetCode)
- 这一题最难的还是找规律,和整数拆分类似,DST定头节点后,左边是小的DST,右边是大的DST,所以可能数是左右可能数相乘
- dp含义:dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]
- 递推公式:dp[i] += dp[j] * dp[i - j - 1](j从0开始)
- 初始化:dp[0] = dp[1] = 1,从前往后遍历
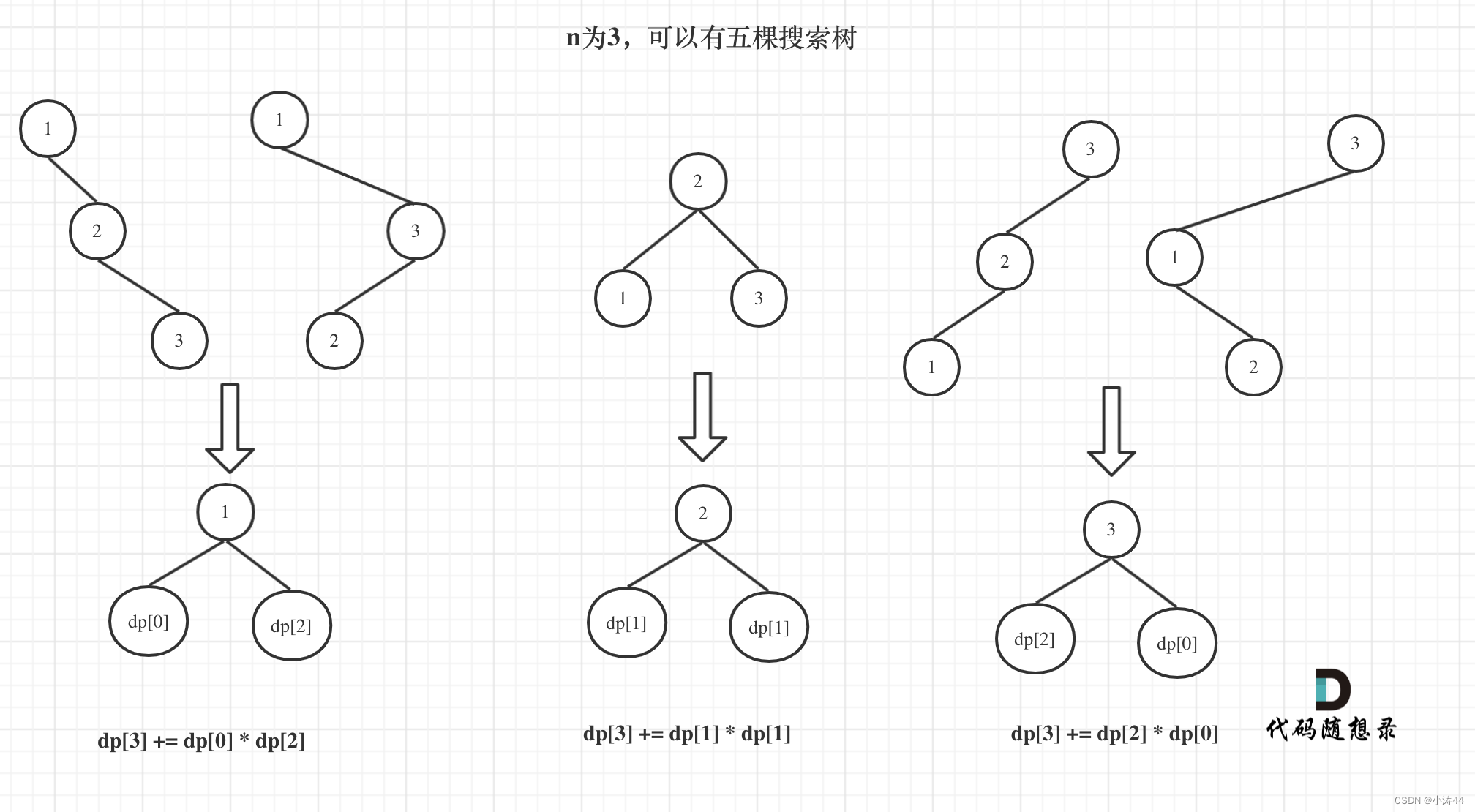
-
class Solution { public:int numTrees(int n) {vector<int> dp(20);dp[0] = 1;dp[1] = 1;for(int i = 2; i < dp.size(); i++){for(int j = 0; j < i; j++){dp[i] += dp[j] * dp[i - j - 1];}}return dp[n];} };
01背包问题理论基础(二维数组)
- 问题定义
- 有限个物体(都只有一个),有大小和价值,放进固定容量的背包里如何放是最大价值,暴力算的话时间复杂度为2^n(每件物品状态01),需要用动态规划,刚开始看有点懵,但是结合算法图解看很好懂

- dp数组含义
- dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少

- 递推公式
- dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

- 初始化
- 第一行初始化从能装开始放value[0],第一列and其它全初始化为0

- 遍历顺序
- 两层for循环,按行先遍历物品再遍历背包(反过来其实也行)
- →↓ 或 ↓→(前者好理解一些)
-
void test_2_wei_bag_problem1() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;// 二维数组vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 初始化for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}// weight数组的大小 就是物品个数for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl; }int main() {test_2_wei_bag_problem1(); }
01背包问题理论基础(滚动数组)
- 和二维数组比,一维只要更新一行就行,但是遍历顺序要从后往前(用没更新d[j])
- dp数组含义
- dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
- 递推公式
- dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- 初始化
- 全初始为0,保证用没放物品的值进行更新最大值
- 遍历顺序
- 倒序遍历:本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖

-
void test_1_wei_bag_problem() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;// 初始化vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl; }int main() {test_1_wei_bag_problem(); }
后言
- 正式开始放假!有什么事2024再说!晚上看晚会去咯!看能不能抽到遥遥领先!