使用自相关求周期性

测量不确定性和噪声有时会导致难以发现信号中的振荡行为，即使该震荡行为是预期存在的。

周期信号的自相关序列与信号本身具有相同的周期特征。因此，自相关可以帮助验证周期的存在并确定其持续时间。

以由办公楼内温度计采集的一组温度数据为例。该设备每半小时读取一次读数，持续读取四个月。加载数据并对其绘图。减去均值以重点关注温度波动。将温度转换为摄氏度。测量时间以天为单位。因此，采样率为 2 次测量/小时 × 24 小时/天 = 48 次测量/天。

load officetemptempC = (temp-32)*5/9;tempnorm = tempC-mean(tempC);fs = 2*24;
t = (0:length(tempnorm) - 1)/fs;plot(t,tempnorm)
xlabel('Time (days)')
ylabel('Temperature ( {}^\circC )')
axis tight

如图所示：

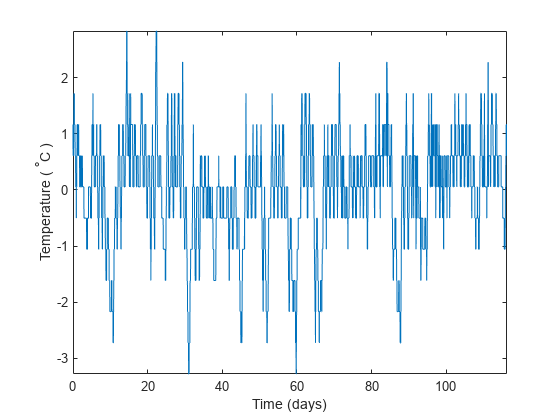
Figure contains an axes object. The axes object with xlabel Time (days), ylabel Temperature ( blank toThePowerOf degree baseline C blank ) contains an object of type line.

温度似乎确实有震荡特性，但周期的长度并不容易确定。

计算温度的自相关性（时滞为零时该值为 1）。将正时滞和负时滞限制为三周。请注意信号的双周期性。

[autocor,lags] = xcorr(tempnorm,3*7*fs,'coeff');plot(lags/fs,autocor)
xlabel('Lag (days)')
ylabel('Autocorrelation')
axis([-21 21 -0.4 1.1])

如图所示：

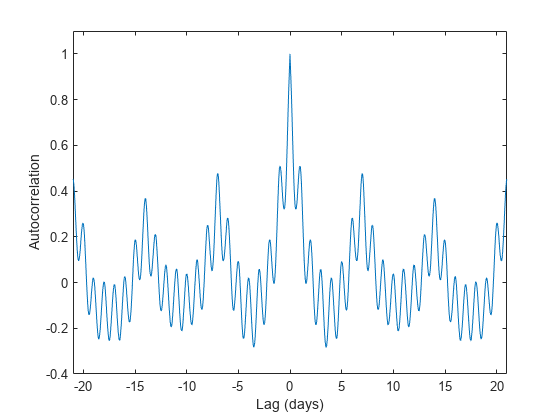
Figure contains an axes object. The axes object with xlabel Lag (days), ylabel Autocorrelation contains an object of type line.

通过找到峰值位置并确定它们之间的平均时间差来确定短周期和长周期。

要找到长周期，请将 findpeaks 限制为只寻找间隔时间超过短周期且最小高度为 0.3 的峰值。

[pksh,lcsh] = findpeaks(autocor);
short = mean(diff(lcsh))/fs
short = 1.0021Get [pklg,lclg] = findpeaks(autocor, ...'MinPeakDistance',ceil(short)*fs,'MinPeakheight',0.3);
long = mean(diff(lclg))/fs
long = 6.9896Get hold on
pks = plot(lags(lcsh)/fs,pksh,'or', ...lags(lclg)/fs,pklg+0.05,'vk');
hold off
legend(pks,[repmat('Period: ',[2 1]) num2str([short;long],0)])
axis([-21 21 -0.4 1.1])

如图所示：

Figure contains an axes object. The axes object with xlabel Lag (days), ylabel Autocorrelation contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Period: 1, Period: 7.