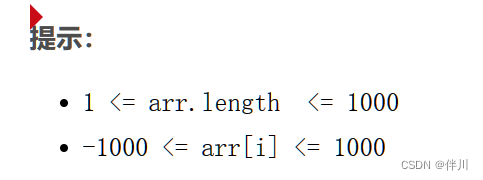S型函数 sigmoid ( x ) = 1 1 + e − x \text{sigmoid}(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1将全体实数 R \text{R} R映射到 ( 0 , 1 ) (0,1) (0,1),称为逻辑函数。其图像为

该函数连续、有界、单调、可微,性质量好。拟合函数为
F ( w ; x ) = sigmoid ( ( x ⊤ , 1 ) w ) = 1 1 + e − ( x ⊤ , 1 ) w F(\boldsymbol{w};\boldsymbol{x})=\text{sigmoid}((\boldsymbol{x}^\top,1)\boldsymbol{w})=\frac{1}{1+e^{-(\boldsymbol{x}^\top,1)\boldsymbol{w}}} F(w;x)=sigmoid((x⊤,1)w)=1+e−(x⊤,1)w1
的回归模型称为逻辑回归模型。其实,逻辑回归模型的拟合函数就是线性回归拟合函数与sigmoid函数的复合。下列代码实现逻辑回归模型
import numpy as np #导入numpy
sigmoid = lambda x: 1/(1 + np.exp(-x)) #逻辑函数
class LogicModel(LineModel): #逻辑模型def F(self, w, x): #重载拟合函数return sigmoid(LineModel.F(self, w, x))
class LogicRegressor(Regression, LogicModel):'''逻辑回归模型'''
程序的第2行将逻辑函数sigmoid实现为Python的lambda表达式。第3~5行表示逻辑模型的LogicModel实现为LineModel类(详见博文《最优化方法Python计算:无约束优化应用——线性回归模型》)的子类。在LogicModel的实现体中,仅在第4~5重载了拟合函数F,即表示为线性模型的拟合函数与sigmoid函数的复合。与Regression类(详见博文《最优化方法Python计算:无约束优化应用——回归模型的测试》)配合即可构成第6~7行的用于预测的逻辑回归模型LogicRegressor类。
例1 电影公司生产的影片的票房收入与该片的拍摄投资和广告推广费用相关。下表给出了5部影片的数据。
| No. | 投资(百万) | 广告(百万) | 票房(百万) |
|---|---|---|---|
| 1 | 6 | 1 | 9 |
| 2 | 9 | 3 | 12 |
| 3 | 12 | 2 | 29 |
| 4 | 14 | 3 | 35 |
| 5 | 16 | 4 | 59 |
设 x = ( x 1 x 2 ) ∈ R 2 \boldsymbol{x}=\begin{pmatrix}x_1\\x_2\end{pmatrix}\in\text{R}^2 x=(x1x2)∈R2,其中, x 1 , x 2 x_1,x_2 x1,x2分别表示影片投资与广告费用, y ∈ R y\in\text{R} y∈R表示影片的票房收入。数据集 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi), i = 1 , 2 , ⋯ , 5 i=1,2,\cdots,5 i=1,2,⋯,5。构成样本特征矩阵 X = ( 6 1 9 3 12 2 14 3 16 4 ) \boldsymbol{X}=\begin{pmatrix}6&1\\9&3\\12&2\\14&3\\16&4\end{pmatrix} X= 6912141613234 ,标签向量 y = ( 9 12 29 35 59 ) \boldsymbol{y}=\begin{pmatrix}9\\12\\29\\35\\59\end{pmatrix} y= 912293559 。假定新影片的拍摄投资 x 1 = 10 x_1=10 x1=10,广告费用 x 2 = 3 x_2=3 x2=3,预测票房价值 y y y。如果拍摄投资 x 1 = 18 x_1=18 x1=18,广告费用 x 2 = 6 x_2=6 x2=6呢?
解:下列代码用给定数据训练逻辑回归模型类LogicRegressor对象,并计算预测票房。
import numpy as np #导入numpy
x = np.array([[6, 1], #设置训练数据[9, 3],[12, 2],[14, 3],[16, 4]])
y = np.array([9, 12, 29, 35, 59])
movi = LogicRegressor() #创建逻辑回归模型
movi.fit(x, y) #训练模型
x1 = np.array([[10, 3], #设置预测数据[18, 6]])
print('对新的影片数据x1')
print(x1)
print('预测票房分别为:%s'%movi.predict(x1)) #预测
就这么简单,看官借助注释信息不难理解代码意义。运行程序,输出
训练中...,稍候
14次迭代后完成训练。
对新的影片数据x1
[[10 3][18 6]]
预测票房分别为:[14.4999173 56.96081974]