马氏距离(Mahalanobis Distance)是一种距离的度量，可以看作是欧氏距离的一种修正，修正了欧式距离中各个维度尺度不一致且相关的问题。

 

马氏距离（Mahalanobis Distance）是由马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。
对于一个均值为μ = ( μ 1 , μ 2 , μ 3 , . . . , μ p ) T μ=(μ_1,μ_2,μ_3,...,μ_p)^Tμ=(μ1​,μ2​,μ3​,...,μp​)T，协方差矩阵为S SS的多变量x = ( x 1 , x 2 , x 3 , . . . , x p ) T x=(x_1,x_2,x_3,...,x_p)^Tx=(x1​,x2​,x3​,...,xp​)T，

马氏距离为：

我们可以发现如果Σ^(-1)是单位阵的时候，马氏距离简化为欧氏距离。

 

那我们为什么要用马氏距离呢？
马氏距离有很多优点： 马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；

由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。

马氏距离还可以排除变量之间的相关性的干扰。

 

下面我们来看一个例子：
如果我们以厘米为单位来测量人的身高，以克（g）为单位测量人的体重。每个人被表示为一个两维向量，如一个人身高173cm，体重50000g，则这个人的身高体重信息可以表示为（173,50000），根据身高体重的信息来判断体型的相似程度。

我们已知小明（160,60000）；小王（160,59000）；小李（170，60000）。根据常识可以知道小明和小王体型相似。但是如果根据欧几里得距离来判断，小明和小王的距离要远远大于小明和小李之间的距离，即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。

以克（g）为单位测量人的体重，数据分布比较分散，即方差大，而以厘米为单位来测量人的身高，数据分布就相对集中，方差小。

马氏距离的目的就是把方差归一化，使得特征之间的关系更加符合实际情况。

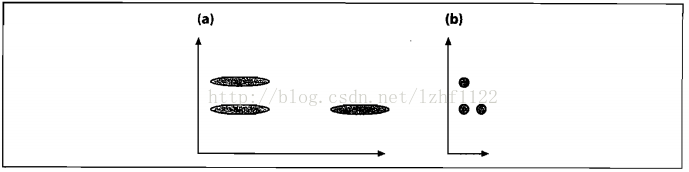
下图（a）展示了三个数据集的初始分布，看起来竖直方向上的那两个集合比较接近。

在我们根据数据的协方差归一化空间之后，如图（b），实际上水平方向上的两个集合比较接近。

 

深入分析：
当求距离的时候，由于随机向量的每个分量之间量级不一样，比如说x1可能取值范围只有零点几，而x2有可能时而是2000，时而是3000，因此两个变量的离散度具有很大差异
马氏距离除以了一个方差矩阵，这就把各个分量之间的方差都除掉了，消除了量纲性，更加科学合理。

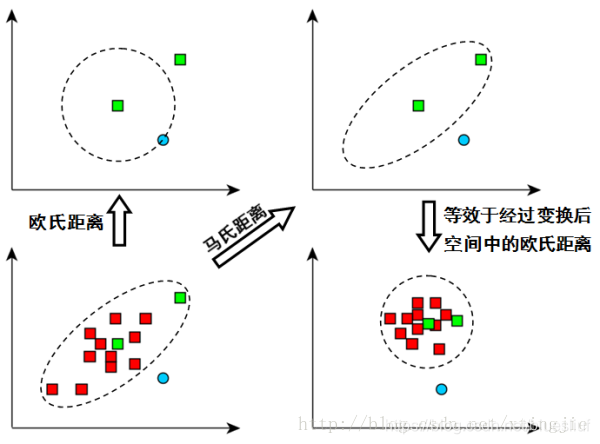
如上图，看左下方的图，比较中间那个绿色的和另外一个绿色的距离，以及中间绿色到蓝色的距离

如果不考虑数据的分布，就是直接计算欧式距离，那就是蓝色距离更近

但实际上需要考虑各分量的分布的，呈椭圆形分布

蓝色的在椭圆外，绿色的在椭圆内，因此绿色的实际上更近

马氏距离除以了协方差矩阵，实际上就是把右上角的图变成了右下角

 

推荐文章：马氏距离(Mahalanobis Distance)

参考文献：

https://blog.csdn.net/bluesliuf/article/details/88862918?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control