平衡二叉树的定义:

 为避免树的高度增长过快，降低二叉排序树的性能，规定在插入和删除二叉树结点时，要保证任意结点的左、右子树高度差的绝对值不超过1，将这样的二义树称为平衡二叉树AVL (Balanced Binary Tree),简称平衡树。

平衡二叉树的插入:

(1) LL平衡旋转(右单旋)

由于在结点A的左孩子(L的在子树(L上插入了新结点，A的平衡因子由1增至2，导致以A为根的子树大去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树。
如图7.11所示，结点旁的数值代表结点的平衡因子，而用方块表示相应结点的子树，下方数值代表该子树的高度。 

 

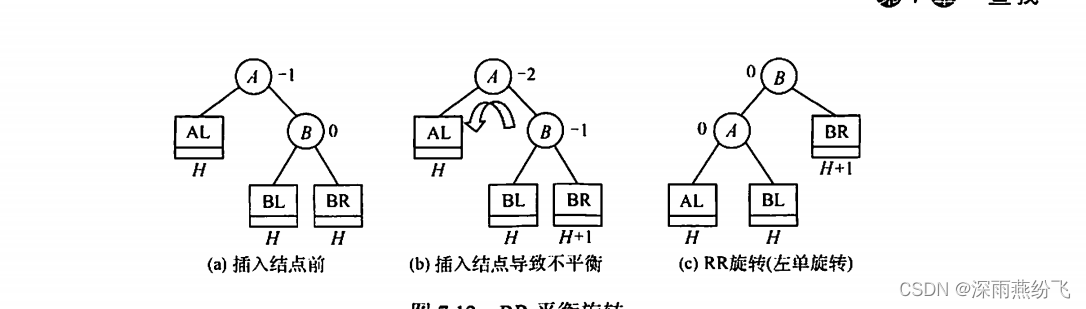
(2) RR平衡旋转(左单旋转)

由于在结点A的右孩子(R)的右子树(R)上插入了新结点，A的平衡因子由-1减至-2,导致以A为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树.

 

(3) LR平衡旋转(先左后右旋转)

由于在A 的左孩子(L)的右子树(R)上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后把该C结点向右上旋转提升到A结点的位置.

 

 (4)RL平衡旋转(先右后左双旋转)

 由于在A的右孩子(R)的左子树(L)上插入新结点，A的平衡因子由-1减至-2,导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后把该C结点向左上旋转提升到A结点的位置.

  

 1.定义结构体

typedef struct TreeNode
{int data;//定义数据域 int height;//定义高度 struct TreeNode *lchild;//左孩子 struct TreeNode *rchild;//右孩子 
}TreeNode;

 2.获取结点高度

int getHeight(TreeNode *node)
{return node ? node->height : 0;//判断node是否为空,为空返回0,不为空返回高度 
}

 3.取最大值

int max(int a,int b)
{return a > b ? a : b;
}

 4.RR平衡旋转(向左旋转一次)

void rrRotation(TreeNode *node,TreeNode **root)
{/*参数一node:代表该结点
参数二root:代表父结点结点*/TreeNode *temp = node->rchild;//右孩子保存给中间指针 node->rchild = temp->lchild;//node的左孩子赋值给node的右孩子 temp->lchild = node;//node代替node的左孩子 node->height = max(getHeight(node->lchild),getHeight(node->rchild))+1;//最大值加一 temp->height = max(getHeight(temp->lchild),getHeight(temp->rchild))+1;*root = temp;
}

5.LL平衡旋转(向右旋转一次)

void llRotation(TreeNode *node,TreeNode **root)
{/*参数一node:代表该结点
参数二root:代表父结点结点*/TreeNode *temp = node->lchild;node->lchild = temp->rchild;temp->rchild = node;node->height = max(getHeight(node->lchild),getHeight(node->rchild))+1;temp->height = max(getHeight(temp->lchild),getHeight(temp->rchild))+1;*root = temp;
}

 6.建立平衡二叉树

void avlInsert(TreeNode **T,int data)
{/*第一个参数**T:双重解引用,用于更改T中的值
第二个参数data:用于传递元素并比较大小*/if(*T==NULL)//首先判断该结点是否为空,是空结点则新建结点并初始化{*T = (TreeNode*)malloc(sizeof(TreeNode));//申请内存空间 (*T)->data = data;//写入数据(*T)->height = 0;//高度初始化为0 (*T)->lchild = NULL;//左孩子初始为空(*T)->rchild = NULL;//右孩子初始为空 }else if(data<(*T)->data)//data小于当前结点值 {avlInsert(&(*T)->lchild,data);//要插入的元素比结点内的元素小,则往左子树走//拿到当前左右子树的高度 int lHeight = getHeight((*T)->lchild);int rHeight = getHeight((*T)->rchild);if(lHeight-rHeight==2)//判断二叉树是否失衡 {//判断高度差 if(data<(*T)->lchild->data)//要插入的元素小于当前结点左孩子的元素 {//LL型  llRotation(*T,T);//右旋一次	}else{//LR型 rrRotation((*T)->lchild,&(*T)->lchild);//先左旋 llRotation(*T,T);//后右旋 }			}}else if(data>(*T)->data)//data大于当前结点值 {avlInsert(&((*T)->rchild),data);//要插入的元素比结点内的元素大,则往右子树走//拿到当前左右子树的高度 		int lHeight = getHeight((*T)->lchild);int rHeight = getHeight((*T)->rchild);if(rHeight-lHeight==2)//判断二叉树是否失衡 {//判断高度差 if (data>(*T)->rchild->data){//RR型 rrRotation(*T,T);//左旋一次 }else{//RL型 llRotation((*T)->rchild,&(*T)->rchild);//先右旋 rrRotation(*T,T);//后左旋 } }}(*T)->height = max(getHeight((*T)->lchild),getHeight((*T)->rchild))+1;
}

7.前序遍历(根左右)

void preOrder(TreeNode *T)
{if(T){printf("%d ",T->data);//输出根结点preOrder(T->lchild);//递归遍历左子树preOrder(T->rchild);//递归遍历右子树}
}

8.主函数

int main()
{TreeNode *T = NULL;//初始树根结点 int nums[5] = {1,2,3,4,5};int i;for(i=0;i<5;i++)avlInsert(&T,nums[i]);//构造平衡二叉树 preOrder(T);printf("\n");return 0;
}

 完整代码:

#include <stdio.h>
#include <stdlib.h>
/*定义结构体*/
typedef struct TreeNode
{int data;//定义数据域 int height;//定义高度 struct TreeNode *lchild;//左孩子 struct TreeNode *rchild;//右孩子 
}TreeNode;
/*获取结点高度*/
int getHeight(TreeNode *node)
{return node ? node->height : 0;//判断node是否为空,为空返回0,不为空返回高度 
}
/*取最大值*/
int max(int a,int b)
{return a > b ? a : b;
}
/*RR平衡旋转(向左旋转一次)*/
void rrRotation(TreeNode *node,TreeNode **root)
{/*参数一node:代表该结点
参数二root:代表父结点结点*/TreeNode *temp = node->rchild;//右孩子保存给中间指针 node->rchild = temp->lchild;//node的左孩子赋值给node的右孩子 temp->lchild = node;//node代替node的左孩子 node->height = max(getHeight(node->lchild),getHeight(node->rchild))+1;//最大值加一 temp->height = max(getHeight(temp->lchild),getHeight(temp->rchild))+1;*root = temp;
}
/*LL平衡旋转(向右旋转一次)*/
void llRotation(TreeNode *node,TreeNode **root)
{/*参数一node:代表该结点
参数二root:代表父结点结点*/TreeNode *temp = node->lchild;node->lchild = temp->rchild;temp->rchild = node;node->height = max(getHeight(node->lchild),getHeight(node->rchild))+1;temp->height = max(getHeight(temp->lchild),getHeight(temp->rchild))+1;*root = temp;
}
/*建立平衡二叉树*/
void avlInsert(TreeNode **T,int data)
{/*第一个参数**T:双重解引用,用于更改T中的值
第二个参数data:用于传递元素并比较大小*/if(*T==NULL)//首先判断该结点是否为空,是空结点则新建结点并初始化{*T = (TreeNode*)malloc(sizeof(TreeNode));//申请内存空间 (*T)->data = data;//写入数据(*T)->height = 0;//高度初始化为0 (*T)->lchild = NULL;//左孩子初始为空(*T)->rchild = NULL;//右孩子初始为空 }else if(data<(*T)->data)//data小于当前结点值 {avlInsert(&(*T)->lchild,data);//要插入的元素比结点内的元素小,则往左子树走//拿到当前左右子树的高度 int lHeight = getHeight((*T)->lchild);int rHeight = getHeight((*T)->rchild);if(lHeight-rHeight==2)//判断二叉树是否失衡 {//判断高度差 if(data<(*T)->lchild->data)//要插入的元素小于当前结点左孩子的元素 {//LL型  llRotation(*T,T);//右旋一次	}else{//LR型 rrRotation((*T)->lchild,&(*T)->lchild);//先左旋 llRotation(*T,T);//后右旋 }			}}else if(data>(*T)->data)//data大于当前结点值 {avlInsert(&((*T)->rchild),data);//要插入的元素比结点内的元素大,则往右子树走//拿到当前左右子树的高度 		int lHeight = getHeight((*T)->lchild);int rHeight = getHeight((*T)->rchild);if(rHeight-lHeight==2)//判断二叉树是否失衡 {//判断高度差 if (data>(*T)->rchild->data){//RR型 rrRotation(*T,T);//左旋一次 }else{//RL型 llRotation((*T)->rchild,&(*T)->rchild);//先右旋 rrRotation(*T,T);//后左旋 } }}(*T)->height = max(getHeight((*T)->lchild),getHeight((*T)->rchild))+1;
}/*前序遍历(根左右)*/
void preOrder(TreeNode *T)
{if(T){printf("%d ",T->data);//输出根结点preOrder(T->lchild);//递归遍历左子树preOrder(T->rchild);//递归遍历右子树}
}
int main()
{TreeNode *T = NULL;//初始树根结点 int nums[5] = {1,2,3,4,5};int i;for(i=0;i<5;i++)avlInsert(&T,nums[i]);//构造平衡二叉树 preOrder(T);printf("\n");return 0;
}

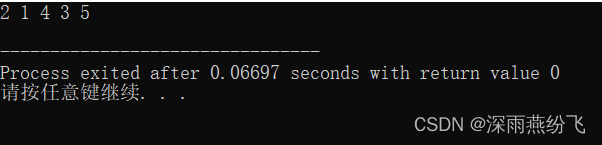
 运行结果: