目录
编辑
一,反转链表
1.题目描述
2.例子
3.题目接口
4.分析以及解题代码
1.迭代法
2.递归写法
二,两两交换两个链表中的节点
1.题目描述
2.例子
3.题目接口
4.题目分析以及解法
一,反转链表
1.题目描述
首先来看看反转链表的题目描述:
给你单链表的头节点
head,请你反转链表,并返回反转后的链表。
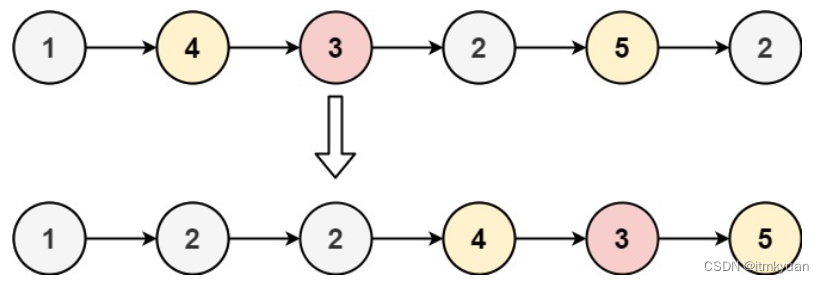
2.例子
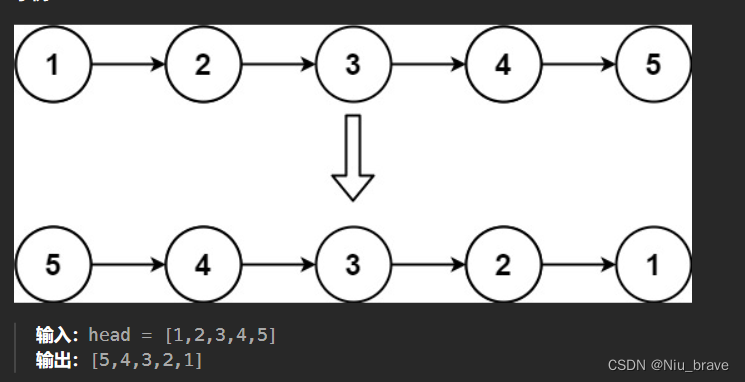
3.题目接口
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {}
};4.分析以及解题代码
1.迭代法
迭代法可谓是比较简单并且好理解的方法了。大概的思路便是定义三个指针,pre,cur,next。然后通过这三个指针来调整节点的指向。代码如下:
class Solution { public:ListNode* reverseList(ListNode* head) {if(head == nullptr||head->next == nullptr){return head;}ListNode* pre = nullptr;ListNode*cur = head;ListNode* next = head->next;while(cur)//不断迭代{cur->next = pre;pre = cur;cur = next;if(cur){next = cur->next;}}return pre;} };看起来迭代法不错,代码也挺简洁的。但是这道题其实还可以用递归来解决,用递归写出来的代码会更加简洁。但是递归写法的代码通常会比较难以理解。
2.递归写法
反转链表这个大任务的实现卡其实是有赖于许多个小任务的实现来完成的,这些小任务的操作又是重复的。所以在这里便会出现重复的子问题,有重复的子问题便有递归的解决方法。
1.重复的子问题:如以上例子,要反转的链表是一个带有五个节点的链表。要反转这五个节点首先就得后面四个节点,要反转后面四个链表就得反转后面的两个节点。
2.递归出口:在反转链表时,如果遇到空节点或者是只有一个节点时就不用反转了。这时直接返回头节点便是了。
3.函数体书写:函数体的书写其实是针对一个子问题来解决的。就比如最小的两个节点,要反转链表便是让头结点的下一位节点的next指向头节点,而让头节点的next指向nullptr。并且要保存最后一个节点并一层一层的返回。
所以递归代码书写如下:
class Solution { public:ListNode* reverseList(ListNode* head) {if(head == nullptr||head->next == nullptr){return head;}ListNode* newhead = reverseList(head->next);//保存最后一个节点head->next->next = head;//从最后的两个链表开始不断地从后往前反转链表head->next = nullptr;return newhead;//返回的一直都是最后一个节点} };递归的代码虽然有点难以理解但是还是特别神奇的。
二,两两交换两个链表中的节点
1.题目描述
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
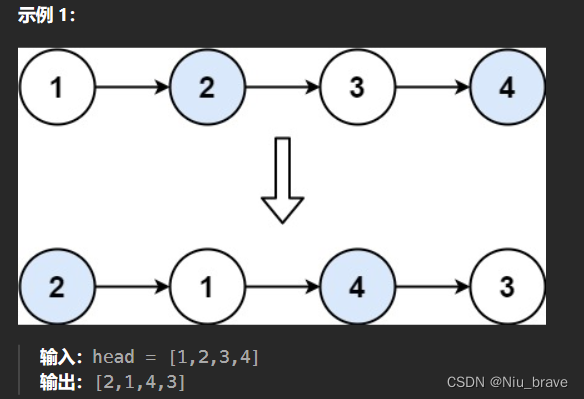
2.例子
3.题目接口
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {}
};4.题目分析以及解法
首先,题目要求的是两两交换节点,所以这个题目的节点的总数就是偶数。所以我们可以大胆的将大问题转换成重复的子问题。
1.子问题就是两个两个为一组交换节点。
2.递归的结束条件就是当传入的节点只有一个或者节点为nullptr时便返回到上层。
3.函数体的书写就要靠函数的实现逻辑了。首先,和反转链表一样得保存上一层的节点。但是这个节点在每一层都会改变成不同的节点。然后便是反转每一层两个节点的指向。然后保存头节点。返回。
代码如下:
class Solution { public:ListNode* swapPairs(ListNode* head) {if(head == nullptr||head->next == nullptr){return head;}ListNode* tmp = swapPairs(head->next->next);//递归回来的一层的头节点ListNode* ret = head->next;//这一层的头节点//反转链表的操作head->next->next = head;head->next = tmp;return ret;//返回这一层的头节点} };