引言
本文介绍本系列的第一个机器学习算法——K近邻算法(K-Nearest Neighbors,knn)。
它的思想很简单,用到的数学知识也比较少(只用到了求距离公式),效果好。
本文还会涉及到和应用机器学习相关的问题的处理方式。
- 上一篇:机器学习入门——numpy与matplotlib的使用简介
- 下一篇:机器学习入门——线性回归
k近邻算法
下面解释下这个算法的思想。我们以一个例子来阐述。
以肿瘤大小和时间作为特征,以良性和恶性作为标签,我们画出下面的图:
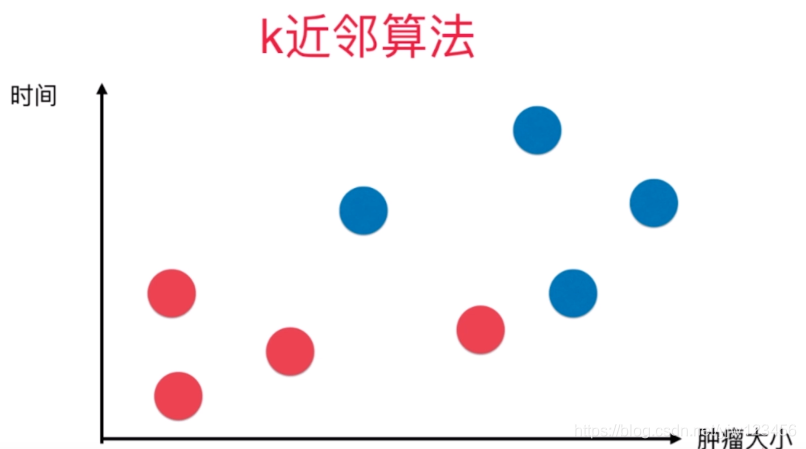
这里用红色表示良性肿瘤,蓝色表示恶性肿瘤。这些作为一个初始信息,假设此时来了一个肿瘤患者,将其映射到上图中得到了下面绿色的点。

此时我们如何判断新来的患者是良性还是恶性(肿瘤)。
如果用k近邻算法来求解的话,我们需要先取一个 k k k值,这里假设为 3 3 3。
对于每个新的数据点,该算法做的事情是,寻找离新的数据点最近的3个点。
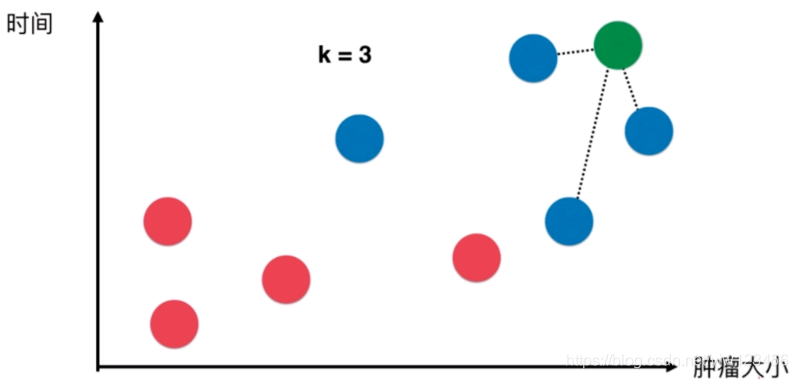
然后最近的点以它们自己的标签进行投票,这里将 k k k设成奇数也是有道理的。
这里最近的3个点都是恶性肿瘤的点,因此k近邻算法就说这个新的数据点很可能是属于恶性肿瘤标签。

k近邻算法认为两个样本足够相似的话,它们就有更高的概率属于同一个类别。
这里用特征空间中的距离来描述相似性。
假设再来了一个新的样本点,下图绿点:
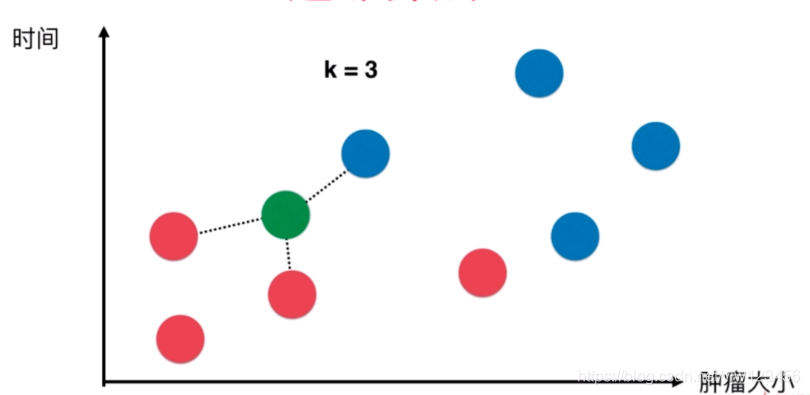
这时,最邻近的点进行投票,其中良性投票:恶性投票为 2 : 1,因此k近邻认为这个样本点更可能属于良性的。
k近邻算法主要解决监督学习中的分类问题。
下面我们通过代码来实现k近邻的思想。
import numpy as np
import matplotlib.pyplot as plt# 这里先用假的数据集
raw_data_X = [[ 3.3935,2.3312],[3.1101,1.7815],[1.3438,3.3684],[3.5823,4.6792],[2.2804,2.8670],[7.4234,4.6965],[5.7451,3.5340],[9.1721,2.5110],[7.7928,3.4241],[7.9398,0.7917]]
raw_data_y = [0,0,0,0,0,1,1,1,1,1] # 0良性肿瘤,1恶性肿瘤
其中大写的X表示矩阵,小写的y表示向量。
我们先绘制散点图,来看数据的分布是怎样的
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)# 分别用不同颜色来绘制不同类别的点
plt.scatter(X_train[y_train == 0,0] ,X_train[y_train==0,1],color='g')
plt.scatter(X_train[y_train == 1,0] ,X_train[y_train==1,1],color='r')
plt.show()
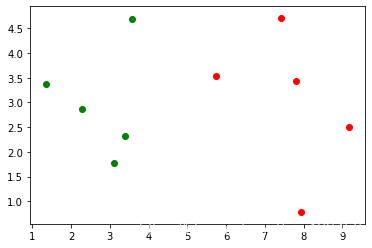
假设此时来了一个新的样本点x = np.array([8.0934,3.3657]),我们如何通过knn来判断其类别。
我们在上面散点图的基础上,增加到新样本的绘制:
x = np.array([8.0934,3.3657]) #新的样本点plt.scatter(X_train[y_train == 0,0] ,X_train[y_train==0,1],color='g')
plt.scatter(X_train[y_train == 1,0] ,X_train[y_train==1,1],color='r')
plt.scatter(x[0],x[1],color='b')
plt.show()

新样本点是上图蓝点,根据knn的思想,我们可以猜到它属于红色样本点类别。
接下来看如何用代码来实现knn的思想。
首先要计算新的样本点与所有原来的点之间的距离。那么怎么计算距离呢,我们用欧几里得距离公式来计算。
d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + … + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 d(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2+…+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^{n}{(x_i-y_i)^2}} d(x,y)=(x1−y1)2+(x2−y2)2+…+(xn−yn)2=i=1∑n(xi−yi)2
在二维平面中,就是 d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 d(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2} d(x,y)=(x1−y1)2+(x2−y2)2
代码实现也很简单(不了解numpy的可以参阅机器学习入门——numpy与matplotlib的使用简介):
distances = []#保存新样本点与原来点的距离
from math import sqrt
for x_train in X_train:d = sqrt(np.sum((x_train - x)**2)) # x_train - x 两个向量对应元素相减,得到一个新的向量,每个元素再求平方,再通过聚合函数得到一个数,最后进行开方distances.append(d)
这样我们就得到了训练数据中的每个点与新样本点之间的距离,接下来找到距离最小的 k k k个点即可。
其实上面的for循环可以用列表推导式简化:
distances = [sqrt(np.sum((x_train - x)**2)) for x_train in X_train]
接下来就是按照距离排序,但是我们知道最小的几个距离是没用的,我们还要知道哪些点与新样本是距离最小的。
此时argsort就可以应用的,它返回的就是索引。
np.argsort(distances)
#array([8, 7, 5, 6, 9, 3, 0, 1, 4, 2], dtype=int64)
从上面可以看到,最近的是索引为8的那个点,其次是7,依此类推。
nearset = np.argsort(distances)
k = 6
topK_y = [y_train[i] for i in nearset[:k]] #i在nearset数组中前k个元素
接下来就计算一下这k个点里面属于哪个类别中的点最多,这里如果用偶数的话,55开怎么办。所以建议取奇数(其实还要考虑类别的个数,如果是3个类别,取奇数9,也有3:3:3的风险,因此k的选择很重要)。
先抛出奇数还是偶数的问题,我们可以用Counter这个类很方便的计算属于哪个类别的多。
from collections import Counter
Counter(topK_y)
# Counter({1: 5, 0: 1})可以看到,5个点投票类别1,1个点投票类别0。
我们可以调用most_common方法得到投票数最多的类别,它返回的是一个元组列表
最终的代码就是:
from collections import Counter
votes = Counter(topK_y)
predict_y = votes.most_common(1)[0][0]
print(predict_y) # 1
得到它的类别为1。我们回过头来看下类别1使用红色点绘制的,和我们的猜想一致。
以上就是简单的用代码实现knn的思想。
我们汇总一下以上的代码,形成一个方法:
def kNN_classify(k,X_train,y_train,x):distances = [sqrt(np.sum((x_train - x)**2)) for x_train in X_train]nearset = np.argsort(distances)topK_y = [y_train[i] for i in nearset[:k]]votes = Counter(topK_y)return votes.most_common(1)[0][0]接下来运行一下
predict_y = kNN_classify(6,X_train,y_train,x)
print(predict_y) # 1
输出为1,没毛病。
我们来回顾下机器学习的流程。
在监督学习算法中,训练数据集通常包含训练数据和数据标签,通过训练算法得到模型的过程叫拟合(fit)。输入样例送给模型后,得到输出结果的过程叫预测(predict)。
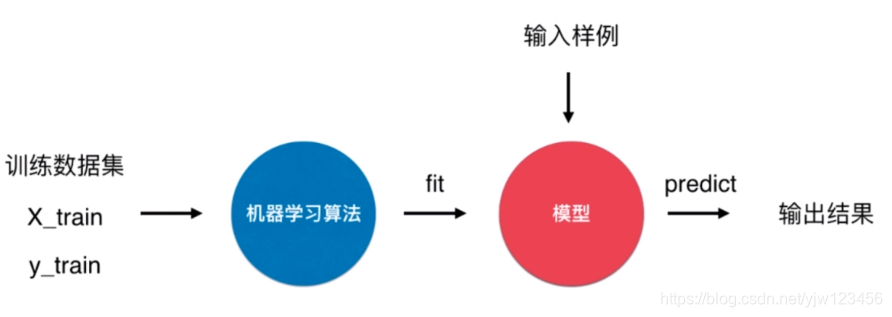
我们把knn算法搬到这个流程里面会发现,knn算法并没有训练得到模型,确实是。可以说knn是一个不需要训练过程的算法。
这样在进行算法抽象,抽象出公共方法的时候就很不爽了。为了和其他算法统一,可以认为训练数据集本身就是knn算法的模型。
我们先来看看sklearn是如何调用knn算分进行预测的。
sklearn中的knn
sklearn采用面向对象的思想,每个算法都是一个类。
from sklearn.neighbors import KNeighborsClassifier
kNN_classifier = KNeighborsClassifier(n_neighbors=6)#这个参数就是k
kNN_classifier.fit(X_train,y_train) #对sklearn中的每个学习算法都需要fit
x = np.array([8.0934,3.3657]) #新的样本点
kNN_classifier.predict(x)
这段代码在新版的sklearn中会报错,在新版的sklearn中,所有的数据都应该是二维矩阵,哪怕它只是单独一行或一列。
ValueError: Expected 2D array, got 1D array instead
array=[8.0934 3.3657].
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
并且上面有解决方法,我们按照它提示的来处理一下。
x = np.array([8.0934,3.3657]).reshape(1, -1)#shape变成了(1, 2)
kNN_classifier.predict(x)
返回的结果是
array([1])
注意它返回的是一个数组,可以同时预测多个样本,这里我们只传入了一个样本(一个一行的矩阵,多行矩阵就是多个样本,用心良苦啊),因此数组中元素个数为1。
可以看到,上面的过程是符合这个图的
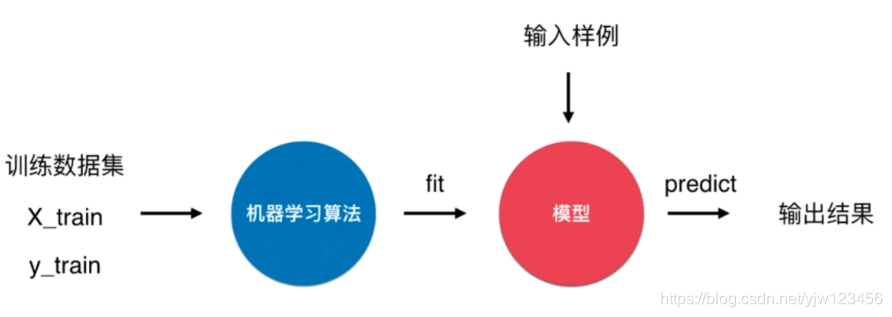
我们也把之前写的代码整理成这种模式。
这里我们继承了BaseEstimator,这意味着它可以在任何使用scikit-learn estimator 的地方使用
import numpy as np
from math import sqrt
from collections import Counterfrom sklearn.base import BaseEstimatorclass KNNClassifier(BaseEstimator):def __init__(self,k):assert k >= 1, "k must be valid"self.k = kself._X_train = Noneself._y_train = Nonedef fit(self,X_train,y_train):assert X_train.shape[0] == y_train.shape[0], \"the size of X_train must be equal to the size of y_train"assert self.k <= X_train.shape[0], \"the size of X_train must be at least k."self._X_train = X_trainself._y_train = y_trainreturn selfdef predict(self,X_predict):assert self._X_train is not None and self._y_train is not None, \"must fit before predict!"# X_predict矩阵的行数无所谓,但是列数必须和训练集中的一样assert X_predict.shape[1] == self._X_train.shape[1], \"the feature number of X_predict must be equal to X_train"y_predict = [self._predict(x) for x in X_predict]return np.array(y_predict)def _predict(self,x):"""给定单个待预测数据x,返回x的预测结果值"""assert x.shape[0] == self._X_train.shape[1], \"the feature number of x must be equal to X_train"distances = [sqrt(np.sum((x_train - x) ** 2))for x_train in self._X_train]nearest = np.argsort(distances)topK_y = [self._y_train[i] for i in nearest[:self.k]]votes = Counter(topK_y)return votes.most_common(1)[0][0]def __repr__(self):return "KNN(k=%d)" % self.k #相当于java toString()接下来应用一下我们刚才写的类:
knn_clf = KNNClassifier(k=6)
knn_clf.fit(X_train,y_train)
X_predict = x = np.array([8.0934,3.3657]).reshape(1, -1)y_predict = knn_clf.predict(X_predict)
y_predict # array([1])到此我们实现了knn算法,但是这个算法的表现如何,准确率高不高呢。接下来一起学习下如何评估算法的表现。
判断机器学习算法的性能
我们先来看下机器学习的过程,首先我们将原始数据都当成训练数据,训练出一个模型,在knn算法中是将新的数据与训练集中所有数据求距离,最后找出前k小的距离。也就是说,我们用全部数据得到的模型来预测新数据所属的类别。
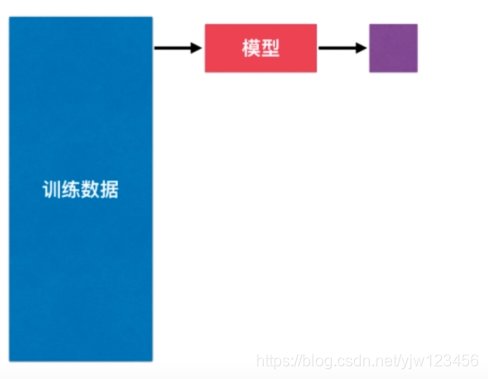
我们得到模型的意义是想在真实环境中使用,现在我们这样做是有很大的问题的。
第一个非常严重的问题是,我们拿所有的训练数据去训练模型,我们只能将这个模型放到真实环境中去使用 了,如果模型很差怎么办?并且真实环境难以拿到真实的标签。
这样我们无法知道我们的模型是好还是坏。
改进这个问题最简单的方法是将训练和测试数据分离。

我们将原始数据的大部分作为训练数据,剩下的一部分作为测试数据。这样我们只用我们的训练数据训练出了模型,我们接下来就可以用没有参与到训练过程的测试数据来测试我们模型的好坏。

因此,我们可以通过测试数据直接判断模型好坏,这样可以在模型进入真实环境前改进模型。
这种方式叫 train test split,其实这种方式还是存在一些问题,但这里先不展开,后面的文章会介绍到。
我们先用这种方式来测试我们之前写好的knn算法。
此时我们用sklearn提供的iris数据集来进行训练:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasetsiris = datasets.load_iris()# 使用iris数据集
X = iris.data # (150, 4)
y = iris.target #(150,)
得到了数据集后,我们就进行训练测试数据分离。
在拆分前一般需要先进洗牌操作,为什么呢,我们可以看下y这个类别向量

可以看到,它是有序的。如果我们直接拿这个数据进行拆分的话,我们得到的训练数据样本分布就很不均匀,这样会导致算法的表现不好。
要注意的是,我们不能单独的对X或y进行洗牌,因为它们是有一一对应的关系的。我们可以对它们的索引进行洗牌:
shuffle_indexs = np.random.permutation(len(X))#对150个连续数进行随机排列
shuffle_indexs

接下来就可以开始拆分了,先指定下作为测试数据集的比例,这里假设20%的数据作为测试数据。
test_ratio = 0.2
test_size = int(len(X) * test_ratio)
test_indexes = shuffle_indexs[:test_size]#前20%是测试数据
train_indexes = shuffle_indexs[test_size:]#后80%是训练数据
得到了这些索引后,我们可以使用花式索引的方式来获取训练数据和测试数据:
X_train = X[train_indexes]
y_train = y[train_indexes]X_test = X[test_indexes]
y_test = y[test_indexes]
拆分好后,我们来看下训练数据的shape:

将上述过程封装成一个函数,以便后面多次调用:
def train_test_split(X,y,test_ratio=0.2,seed=None):if seed:np.random.seed(seed) #支持指定随机种子shuffle_indexs = np.random.permutation(len(X))test_size = int(len(X) * test_ratio)test_indexes = shuffle_indexs[:test_size]train_indexes = shuffle_indexs[test_size:]X_train = X[train_indexes]y_train = y[train_indexes]X_test = X[test_indexes]y_test = y[test_indexes]return X_train,X_test,y_train,y_test接下来我们使用这个方法来对数据集进行拆分,并应用到我们自己写的knn分类算法中:
X_train,X_test,y_train,y_test = train_test_split(X,y) #其他两个参数取默认值print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
knn_clf = KNNClassifier(k=3)
knn_clf.fit(X_train,y_train)
y_predict = knn_clf.predict(X_test)#对所有的test数据进行预测
y_predict

我们将预测的结果与真实标签进行比较,发现只有一个样本判断错误,其他都是判断正确的。

那么如何量化上面这句话呢,就是通过准确率。
sum(y_predict == y_test)/len(y_test)
得出准确率:0.9666666666666667
从这里我们可以看到,虽然knn的思想简单,但是它的准确率还是很高的。
最后我们介绍下skleran中封装的train_test_splilt:
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y)
可以看到使用起来和我们自己写的方法是一样的,因为在设计我们自己的方法的时候其实是参考了sklearn的方法的。
但是test_size这个参数的名称不一样,这里要注意一下:

准确率
在这小节通过sklearn中的手写数字识别数据集来了解下准确率这个指标。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasetsdigits = datasets.load_digits()
digits.keys()
接下来看下它的描述文档,可以看到,有64个像素点,每个像素点的范围是0到16。

X = digits.data
X.shape #(1797, 64) 可以看到实际只有1797个样本
y = digits.target
y.shape # (1797,)
我们可以通过digits.target_names来看下y值的标签是什么:

我们看下前100个数据的标签排列是啥:

可以看到还是有一定规律的。接下来我们可视化一下第0个样本。
some_digit_image = some_digit.reshape(8,8)
plt.imshow(some_digit_image,cmap="binary")
plt.axis('off')#显示坐标轴不好看
plt.show()

还是可以大概看出来是0的样子,正好和它的标签对应。
好了,数据了解的差不多了,接下来我们用knn算法来对它们进行分类。
from sklearn.model_selection import train_test_splitX_train,X_test,y_train,y_test = train_test_split(X,y)knn_clf = KNNClassifier(k=3)#用我们自己写的knn分类器knn_clf.fit(X_train,y_train)y_predict = knn_clf.predict(X_test)y_predict
看以看到,整个流程和其他的数据集一模一样。接下来我们计算下准确率是多少:
sum(y_predict == y_test)/len(y_test)

可以看到准确率高达99.1%
每次分类后都需要计算准确率,因此我们可以把这个代码封装到一个方法中:
def accuracy_score(y_true,y_predict):return sum(y_predict == y_true)/len(y_true)

有时我们并不想知道预测值是怎样的,只对准确率感兴趣。这时可以在我们自己的knn算法中封装一个函数:
def score(self,X_test,y_test):"""根据测试数据集来确定当前模型的准确率"""y_predict = self.predict(X_test)return sum(y_predict == y_test)/len(y_test)
接下来在fit后可以直接调用score来查看分类准确率:

最后我们看下如何用sklearn提供的knn算法实现类完成上面的过程
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_scoreX_train,X_test,y_train,y_test = train_test_split(X,y)
knn_clf = KNeighborsClassifier(n_neighbors=3)knn_clf.fit(X_train,y_train)
y_predict = knn_clf.predict(X_test)accuracy_score(y_test,y_predict)
同样sklearn的分类器中也封装了score方法:

我们回想下knn算法,其中有个k值参数都是我们预先设定的,这个参数就是超参数,在不同的问题中,它的取值究竟取多少合适呢。
超参数
超参数简单的可以理解为运行机器学习算法前需要指定的参数。和超参数相对应的就是模型参数。
模型参数是算法过程中可以自己更新的参数。knn算法没有模型参数,它的k是典型的超参数。还有学习率这个参数也是典型的超参数。
通常说的调参就是调整超参数。调整超参数的方法有领域知识、经验数值以及实验探索。
接下来我们重点看下实验探索超参数是如何做的。
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifierdigits = datasets.load_digits()
X = digits.data
y = digits.targetX_train,X_test,y_train,y_test = train_test_split(X,y,random_state=456)#这里需要定义随机种子,保证每次运行的结果是一样的best_score =0.0 #最好的准确率
best_k = -1 #当前最好的k#我们从[1,10]里面寻找最好的k
for k in range(1,11):knn_clf = KNeighborsClassifier(n_neighbors=k)knn_clf.fit(X_train,y_train)score = knn_clf.score(X_test,y_test)if score > best_score:best_k = kbest_score = scoreprint("best_k=",best_k)
print("best_score=",best_score)这样就实现了寻找最好的超参数k算法。

如果我们找到的最好的k值是10的话,我们就有必要对10以上的数值进行探索。
其实knn算法中还有一个隐藏的超参数。

以上图为例,在之前我们介绍的knn算法中,蓝色会获胜。但是这种情况是忽略了最近节点的距离这个指标的。
从上图可以得知,绿点离红点是最近的,距离只有1,而离蓝点的距离分别是3和4。
那么在这种情况下,是不是红色点的权重要比那两个蓝色点的权重要高一些呢。
这就是knn算法的另一个用法,考虑了距离的权重,通常是将距离的倒数作为权重。距离越小,权重就越大。

当我们考虑距离权重后,结果就不一样了。
考虑了距离后,还能解决在上文中提到的问题:

假设k=3,但此时最近的3个点刚好对应三个类别,相当于平票。这时我们考虑距离的话,可以很容易选出最终胜出的结果。毕竟这种情况下刚好距离也相等的概率是很低的。
如果我们查看sklearn的官方文档,可以看到weights这个参数。

如果传入distance就会考虑距离权重。
那么我们可以继续验证下是考虑距离权重得到的结果好,还是不考虑得到的结果好。
best_score =0.0 #最好的准确率
best_k = -1 #当前最好的k
best_method = ""for method in ['uniform','distance']:#我们从[1,10]里面寻找最好的kfor k in range(1,11):knn_clf = KNeighborsClassifier(n_neighbors=k,weights=method)knn_clf.fit(X_train,y_train)score = knn_clf.score(X_test,y_test)if score > best_score:best_k = kbest_score = scorebest_method = methodprint("best_k=",best_k)
print("best_score=",best_score)
print("best_method=",best_method)

看来这份数据不考虑距离分类表现会更好。
说到距离,很多人都听过曼哈顿距离:

在二维平面上,这两个黑色点的距离就是x方向上的差值加上y方向上的差值。
在上图中,红、蓝、黄三条线都是曼哈顿距离,而绿色的线是欧几里得距离。

对于距离我们可以用曼哈顿距离或欧几里得距离,经过观察我们可以把欧几里得距离里面的括号换成绝对值。

并且改写下开根号的形式:

再和曼哈顿距离进行比较

可以看到会有一些一致性,我们将其推广可以得到:

这个式子就是明可夫斯基距离:

这样我们得到了一个新的超参数p。

我们从skleran的文档中也可以看到,它提供了这个超参数的设置。
我们改下我们的代码,将p也考虑进去,但此时应用的weights参数取值必须是distance:
best_score =0.0 #最好的准确率
best_k = -1 #当前最好的k
best_p = -1#我们从[1,10]里面寻找最好的k
for k in range(1,11):for p in range(1,5):knn_clf = KNeighborsClassifier(n_neighbors=k,weights='distance',p=p)knn_clf.fit(X_train,y_train)score = knn_clf.score(X_test,y_test)if score > best_score:best_k = kbest_score = scorebest_p = pprint("best_k=",best_k)
print("best_score=",best_score)
print("best_p=",best_p)
这个结果乍一看是不是没有上面的好,当然了 ,我们上面已经知道最好的方式是使用uniform而不是distance作为权重。而这里使用的是distance,虽然我们调整了p(其实最后最好的还是2)。
knn其实还有很多超参数,对于这些超参数,我们上面的搜索策略有个名字,叫网格搜索。比如对于k,p这两个参数,就形成了一个k x p这么大的网格。
但是在具体的搜索过程中,会有一些麻烦,比如对于weights参数,当我们使用uniform的时候就与参数p无关,而使用distance的时候就需要调整参数p。
鉴于超参数之间这种相互依赖的关系,我们如何一次性的把这些超参数都列出来,只跑一次程序就能得到超参数的组合呢。
这时就可以调用sklearn为我们封装的网格搜索方法了。
网格搜索
sklearn提供了GridSearchCV,在使用它之前,我们需要定义我们要搜索的参数:
param_grid = [{'weights':['uniform'],'n_neighbors': [i for i in range(1,11)]},{'weights' : ['distance'],'n_neighbors':[i for i in range(1,11)],'p': [i for i in range(1,6)]}
]
可以看到,它是一个字典列表。每个字典对应一组网格搜索,我们这里有两组。
每组网格搜索中都有对应的参数,字典中的键对应的是参数名,值对应的是参数值列表。当weights为distance时,我们多了一个参数p。
下面我们对knn算法进行网格搜索。
knn_clf = KNeighborsClassifier()
from sklearn.model_selection import GridSearchCVgrid_search = GridSearchCV(knn_clf,param_grid)
grid_search.fit(X_train,y_train) #进行网格搜索,会比较耗时

这里可以看到用了将近1分钟。
接着可以通过下面的代码打印出最佳的分类器信息:
grid_search.best_estimator_

这看到结果是weights=distance,p= 3,k=6。
这和我们上面得到的结果是不一样的,这是因为在网络搜索中,用来评价分类准确的方式更加复杂(GridSearchCV:CV for Cross Validation,交叉验证,以后会介绍)。
我们也可以看下这个最好的超参数下的准确率是多少:
grid_search.best_score_

除了可以通过grid_search.best_estimator_查看得到的最好的超参数外,还可以使用grid_search.best_params_

grid_search.best_estimator_其实返回的就是最好的分类器,我们可以用一个变量来保存它。
knn_clf = grid_search.best_estimator_
对于GridSearchCV这个类来说,还可以传入更多的参数,来帮助我们更好的理解搜索过程以及提速。
查阅官网文档我们可以看到这样一个参数

指定的是并行执行的任务数量。默认是1。如果传入-1意味着使用所有的cpu核来处理。
这里我们传入-1试一下,看时间能节省多少。
grid_search = GridSearchCV(knn_clf,param_grid,n_jobs=-1)

最后执行时间只有12秒左右,提升还是很可观的。
还有个参数可以控制搜索过程中输出信息的详细程度,越大的话,就会有越多的信息。

上面我们的搜索过程是没有任何信息的,当我们执行很复杂的算法时,比如要执行几个小时甚至几天的搜索,这时我们就很想知道搜索过程的信息。
grid_search = GridSearchCV(knn_clf,param_grid,n_jobs=-1,verbose=2)

其实在knn中还有更多的超参数,以距离为例,我们是以距离作为相似度度量的。还有下面的方法:

如果想修改相似度度量的话,可以通过knn的metric这个超参数:

它的取值有下面这些:

数据归一化(Feature Scaling)
之前我们在使用knn来完成分类任务时,其实少做了非常重要的一步——数据归一化。
那什么是数据归一化呢,以及为什么要使用呢。这里我们以开头的例子来阐述。

肿瘤大小单位是cm,而发现时间单位是天。从这两个样本来看,肿瘤大小取值1到5;而发现时间是100到200。 如果我们直接对它们进行距离计算的话,得到的结果显然会被发现时间所主导。
( 1 − 5 ) 2 + ( 200 − 100 ) 2 \sqrt{(1-5)^2+(200-100)^2} (1−5)2+(200−100)2
虽然在样本中,5和1相差了5倍,而200和100只相差了1倍。但是由于量纲不同,导致我们的距离主要衡量的是发现天数之间的差值。

如果我们把发现时间的单位改成年的话,此时它们的距离又被肿瘤大小所主导。
如果我们不进行一些数据的处理的话,直接计算样本之间的距离很有可能是有偏差的。不能非常好的同时反映样本中每个特征的重要程度。
这的数据处理方式就是归一化。现在我们知道了为什么要归一化,那么什么是归一化呢。
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为标量。
其实就是将所有的数据映射到同一尺度上。
最值归一化(normalization)
最简单的归一化方法是最值归一化:将所有数据映射到0-1之间。
它的映射方式很简单:
x s c a l e = x − x m i n x m a x − x m i n x_{scale} = \frac{x - x_{min}}{x_{max} - x_{min}} xscale=xmax−xminx−xmin
它适用于分布有明显边界的情况(要用到最大值和最小值);但是收到outlier(异常点)影响较大。
像学生的成绩是有明显边界的,而收入的分布这种是没有明显边界的。
如果大多数人的收入都是1万元,而有个富豪的收入是100万元,那么大多数人的输入归一化结果是0.01,除了富豪的收入是1。这种归一化结果肯定是非常不好的。
改进方式是使用均值方差归一化。
均值方差归一化(standardization)
均值方差归一化:把所有数据归一到均值为0方差为1的分布中。
这样的结果是,我们的数据并不保证在0到1之间,但是它们的均值都是0,方差都为1。
它适用了数据分布没有明显边界的情况,即有可能存在极端数据值的情况。
哪怕我们的数据有明显边界,使用这种方式效果也是很好的。完胜最值归一化啊。
它的计算方法如下:
x s c a l e = x − x m e a n s x_{scale} = \frac{x -x_{mean}}{s} xscale=sx−xmean
其中 s s s为方差
下面我们来实现一下这两种归一化。
import numpy as np
import matplotlib.pyplot as pltx = np.random.randint(0,100,size=100)#随机生成[0,100)之间的随机数 ,生成100个
x
先生成数据

接下来先实现最值归一化。
(x - np.min(x)) / (np.max(x) - np.min(x))

min,max聚合函数返回的都是一个数; x是一个向量,x减去一个数就是用向量中每个元素都减去一个数,除以一个数也是一样。
这样我们就得到了最值归一化后的向量 x x x。
对于矩阵也是一样
X = np.random.randint(0,100,(50,2)) # 50x2矩阵
X = np.array(X,dtype=float)#将整型数组改成浮点型
# 先处理第0列
X[:,0] = (X[:,0] - np.min(X[:,0])) / (np.max(X[:,0]) - np.min(X[:,0]))
# 再处理第1列
X[:,1] = (X[:,1] - np.min(X[:,1])) / (np.max(X[:,1]) - np.min(X[:,1]))
X[:10,:]

还可以绘制散点图来观察两个维度的分布。
plt.scatter(X[:,0],X[:,1])
plt.show()

可以看到它们都是0到1之间了。
接下来实现均值方差归一化
X2 =np.random.randint(0,100,(50,2))
X2 = np.array(X2,dtype=float)#将整型数组改成浮点型
X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0])
X2[:,1] = (X2[:,1] - np.mean(X2[:,1])) / np.std(X2[:,1])X[:10,:]

同样绘制散点图:
plt.scatter(X2[:,0],X2[:,1])
plt.show()

可以看到x的取值范围大致是在-2.0到1.5之间;而y是-2.0到2.0之间。

我们看下这两列的均值和方差,发现还是符合均值方差归一化的性质的。
sklearn中的Scaler
上节中介绍了将数据归一化的两种方式,具体的在将这种归一化的算法应用到我们机器学习的过程中的时候,有一个很重要的注意事项。
我们把数据集分为训练数据集和测试数据集,在应用均值方差归一化时,对于训练数据,需要求出来训练集中的均值mean_train和方差std_train。
当我们归一化后,我们用归一化后的训练数据集进行训练模型,最终在预测数据的时候,对于测试数据集,我们也要进行相应的归一化处理。
那么问题来了,如果对测试数据进行归一化呢,是不是只要针对测试数据计算出它们的均值和方差,然后得到归一化结果进行预测就行了呢?

这样是不对的。正确的做法是使用训练数据集得到的均值和方差对测试数据进行归一化。

因为我们训练出来的模型要使用在真实环境中,而在真实环境中有时是无法得到所有测试数据相应的均值和方差的。
通常在预测时,每次只有一个样本进来,对于这个样本我们是不知道它的均值和方差的。
同时对数据的归一化也是算法的一部分,对于所有的数据应该使用同样的方式来进行处理。
因此我们需要保存训练数据集得到的均值和方差。
对于归一化这个操作,sklearn中封装了Scaler这个类。在sklearn中,它会让Scaler这个类和我们的机器学习算法类的使用流程保持一致。

上图就是Scaler类的流程。其中的fit就是求出训练数据的均值和方差,然后将其保存。
当其他的样例进来时,Scaler可以很容易的对其进行转换(transform),得到相应的输出结果(归一化后的数据)。
整个流程就是将机器学习算法中的预测改成了转换。
下面我们使用代码来感受一下。
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X[:10,:]

我们从前10份数据可以看到,它的特征并没有进行归一化处理。这里我们对它进行归一化。
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler # 引入sklearn的归一化类X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=456)#这里需要定义随机种子,保证每次运行的结果是一样的standardScaler = StandardScaler()
standardScaler.fit(X_train)
现在我们的standardScaler 就存放了归一化的关键信息。
我们可以查看下它保存的均值和方差:

现在就可以用transform这个方法来对数据进行归一化处理了
X_train = standardScaler.transform(X_train) #保存归一化后的结果
X_test_standard = standardScaler.transform(X_test)
然后我们可以用归一化后的数据进行分类,看效果如何了
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train,y_train)
knn_clf.score(X_test_standard,y_test)

准确率成了100%了!因为我们的数据集比较小,而且区分度较大。
这里要注意的事,对于测试数据也要先进行归一化之后再传入。
在本节的最后,我们尝试下实现自己的StandardScaler。
import numpy as npclass StandardScaler:def __init__(self):self.mean_ = Noneself.scaler_ = Nonedef fit(self,X):"""根据训练数据集X获得数据的均值和方差"""self.mean_ = np.array([np.mean(X[:,i]) for i in range(X.shape[1])])self.scale_ = np.array([np.std(X[:,i]) for i in range(X.shape[1])])return selfdef transform(self,X):resultX = np.empty(shape=X.shape,dtype=float)for col in range(X.shape[1]):resultX[:,col] = (X[:,col] - self.mean_[col]) / self.scaler_[col]return resultX
本文只使用了sklearn中的均值方差归一化,它也提供了最值归一化类MinMaxScaler。
总结
本文介绍了下k近邻算法,它是天然可以解决多分类问题的算法,思想简单,效果也不过。然后我们还介绍了如何调整超参数、判断机器学习的性能,最后探讨了如何通过数据归一化提升我们模型的准确率。
金无足赤人无完人,算法也一样。它不可能只有优点,没有缺点的。k近邻算法最大的缺点是效率低下。想想看,如果训练集中有 m m m个样本, n n n个特征,预测每个新的数据,需要 O ( m n ) O(mn) O(mn)的时间复杂度。
对于这个缺点,有一些优化的方法。比如KD-Tree,Ball-Tree等。可以更快的求出k个近邻点,即使如此,它的效率依然还是很低下。
它还有一个缺点是对异常数据敏感。如果最邻近的节点刚好是异常数据,那么结果必然是错误的。
还有个更大的缺点是维数灾难。而k近邻算法又非常依赖于距离的计算,使得处理高维数据时很可能收到维数灾难。
维数灾难:随着维度的增加,看似相近的两个点之间的距离越来越大

维数灾难有个解决方法就是降维,常用的是PCA降维。这个后面会介绍。
文章的最后,回顾下机器学习流程

接下来要学习的是最简单的处理回归问题的算法——线性回归算法。
参考
1.Python3入门机器学习