前言

我们都知道计算机是用 2进制来表示的，也就是一堆的0 1代码组成的逻辑电路，可是当我们窥探内存的时候，计算机给我们显示的总是 16进制的数字，这使得我们作为人类来说，只熟悉 10进制的，阅读这 16进制，和 2进制时候有一定的困难，并没有准确的概念可言。就比如说，我们可以一眼就直到 10进制的 3217 这个数字的到底可以有多大的印象，而我们却很难清楚知道 2进制的 110010010001 和 16进制的 C91，到底表示有多大的概念，也没有形象的认识，或者说其他进制转化到 10进制时候总是卡顿，伴随着 10进制转化其他进制也不怎么会，忘记如何转;其实
3217 和 110010010001 和 C91 是相等的；。所以这篇文章主要的是想清楚的的看到不同的进制时候能够有一个清晰的认识，能够知道该数字有多大的概念，如何优雅从容的玩转进制的转换。

👀1 .如何理解十进制

当我们看到一个数是 3217的时候，我们是如何理解的？
我们可以做一个简单的等价替换：
3217 = 3×10³+2×10²+1×10¹+7×10⁰ ；
3217 = 3×1000+2×100+1×10+7×1 ；
那是不是说明：
10⁰ = 1
10¹ = 10
10² = 100
10³ = 1000
那是不是说明，我看到任何一个 10进制的数字，都可以拆解为：每个位上的数×10^n-1，再累加和。
是的，是可以，可是10进制那么简单，被你拆解那么难，搞得那么复杂，为啥？
其实我就是想说明一个问题：
！！！重要事情说三遍！！！
在任何进制上的数字上，每一个位，都有自己代表的意义
在任何进制上的数字上，每一个位，都有自己代表的意义
在任何进制上的数字上，每一个位，都有自己代表的意义

就像我们 10进制的 3217 数字，每一个位都表示不同的大小：（数字从右往左数）

第一个位置表示 10⁰ = 1，
第二个位置表示 10¹ = 10，
第三个位置表示 10² = 100，
第四个位置表示 10³ = 1000；
……

---

那我们推广到 2 进制： 二进制的：

第一个位置表示 2⁰ = 1
第二个位置表示 2¹ = 2
第三个位置表示 2² = 4
第四个位置表示 2³ = 8
……

---

那我们推广到 16进制： 二进制的：

第一个位置表示 16⁰ = 1
第二个位置表示 16¹ = 16
第三个位置表示 16² = 256
第四个位置表示 16³ = 4096
……

---

等等 推广任何进制都是一模一样的，都是按照这个规律：然后每个位上的数×m^n-1(m表示进制大小，n表示数字的位数的个数)，再累加和，就得到了，任何进制到10进制的过程。

有了上述的基础，是为了让你如何转换快速转换进制的。

---

👀2. 十进制快速转换二进制的方法

普通的取余法我就不讲了，可以自己百度一下哈；
就比如我要 知道 78 的二进制是多少？如何快速转换呢？
直接看步骤：

第一步：先画一个数轴：（方向从右到左） ；
第二步：在数轴的每个位置上标上 它代表的意义；
第三步：在数轴上找数字（一般都是从数轴较大的数字开始从左往右开始找数字相加），凑数相加，在找到的每个位置上 填写 1 ，没有数字的位置上填写0；
第四步：读取填写位置的数字就是 你所要的二进制；

如下图：
数轴上面可以填 0 到 1；
数轴下面填写每个位置代表的意义

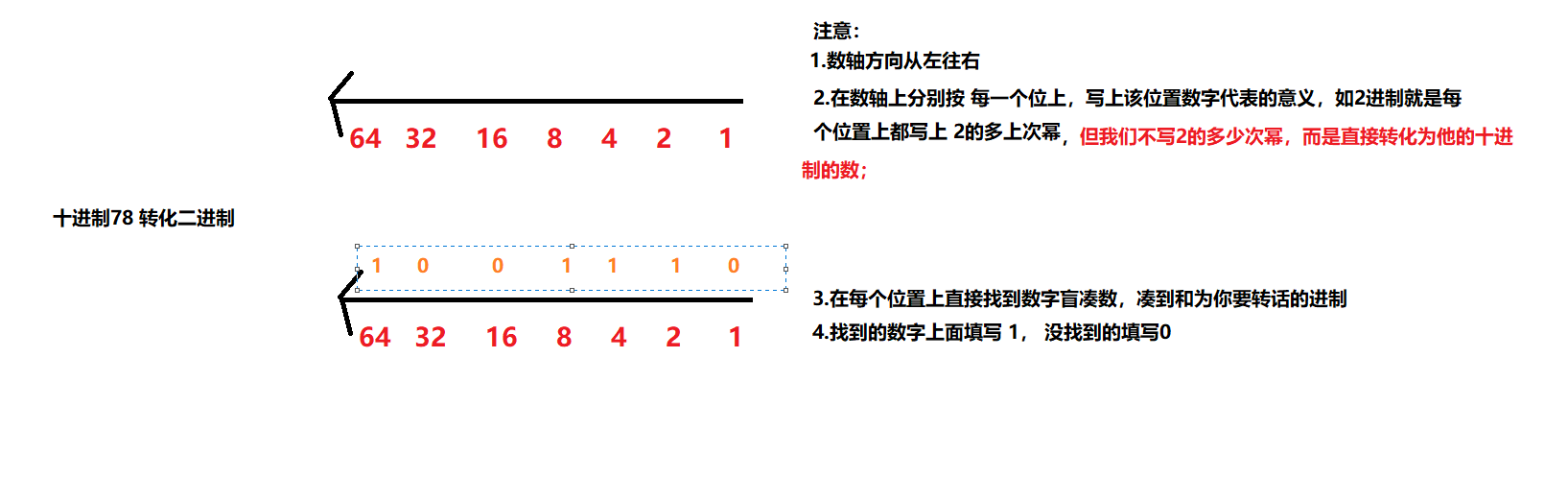
那么我们就直接找到 78 对应的 二进制是 1001110 了；
应该比 取余法快吧，你们可以下去练习一下：其他数字。

---

👀3 .十进制快速转化为十六进制的方法

其实方法和 十进制转化为 二进制差不多；
比如我们还是 用十进制 78 做例子：
如下图：
数轴上面可以填写 0 到 F ;
数轴下面可以填写每个位置

---

👀4 .二进制转化为十进制的快速转换

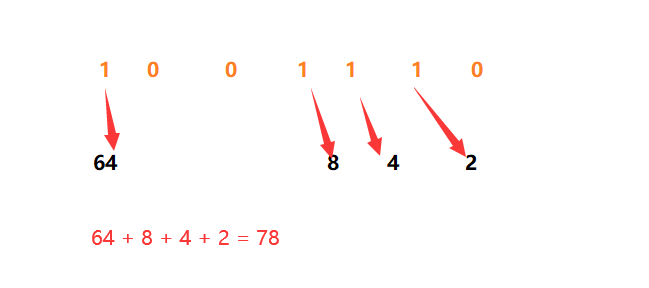
如：二进制：1001110 转化为 十进制？

步骤：

第一步：先确定 二进制的 1 的位置 在哪儿，
第二步：写出有 1 位置上的代表的数字意义是多少
第三步：把 每1 位置上的意义数字相加
第四步：读出十进制数字

如 下图：

👀5. 二进制转化为十六进制的快速转换

如 ：二进制：1001110 转化为十六进制？
步骤：

1. 把 二进制先分为 4 个 数字，4个数字作为一块，从右往左分，不够的补上0；
   2.在每一块上，记住一个数字 1111代表 15，用15去每一块数字上面没有 1 的位置意义数字
   3.把每一块的数字写下来，直接就是16进制了。

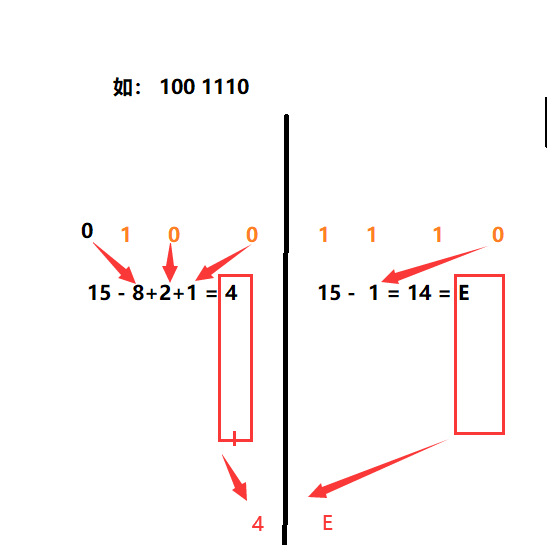
所以该 十六进制为：4E;

---

👀6. 十六进制转换为二进制的快速转换

如 4E;
步骤：

1. 把十六进制数字 先分为每 1 个数字一块，
2. 在 每把每一块的数字当作十进制的数字，直接转化为 2进制，这个办法就是10进制快速转化为 2进制的办法咯。
3. 转化为2进制后，在每一块上不够4位数的要补在高位上0；
4. 读取二进制数字

如下图：

👀7. 总结

快速转化不是看一遍就可以的了，这个需要多次练习，熟悉过程，步骤只是给你看看如何操作，并不是为了让你记住步骤，不要可以记住步骤，要可以记住你是如何操作转化那个动作，也就是你在练习时候的动作，过程，多次练习，你也会用。