概要

在工业上，会有各种读取环境温度，或读取目标物体温度的需求，通常用到的方案有：传感器测温；热敏电阻测温等。本篇着重讲解使用热敏电阻测温的方法。

热敏电阻

何为热敏电阻？热敏电阻即为热电偶传感器，也称为NTC，自身的阻值会随着环境温度的改变而改变，且为非线性变化，某品牌的热敏电阻阻值表如下所示，可见该热敏电阻本身有一定的设计误差，在同一温度下，由于设计误差导致的温度读取差异可在25℃到30℃之间可达到±0.3℃左右。

该热敏电阻大致温度-电阻曲线如下图所示。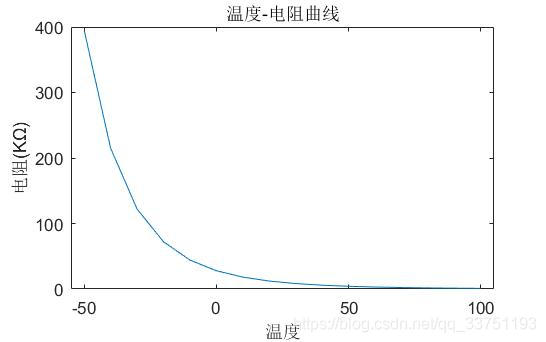
由图可见，想要精确获取温度值，应先获取电阻值，然后使用拟合法，对温度-电阻曲线进行拟合，根据拟合后的函数关系以及当前热敏电阻的电阻值，运算出相应的温度值。

电路设计

热敏电阻采样电路如图所示，使用电阻分压的形式，将热敏电阻的变化通过电压的变化表现出来，再经过电压跟随器进行稳定，并用低通滤波器进行滤波，此处也可用软件滤波进行滤波。

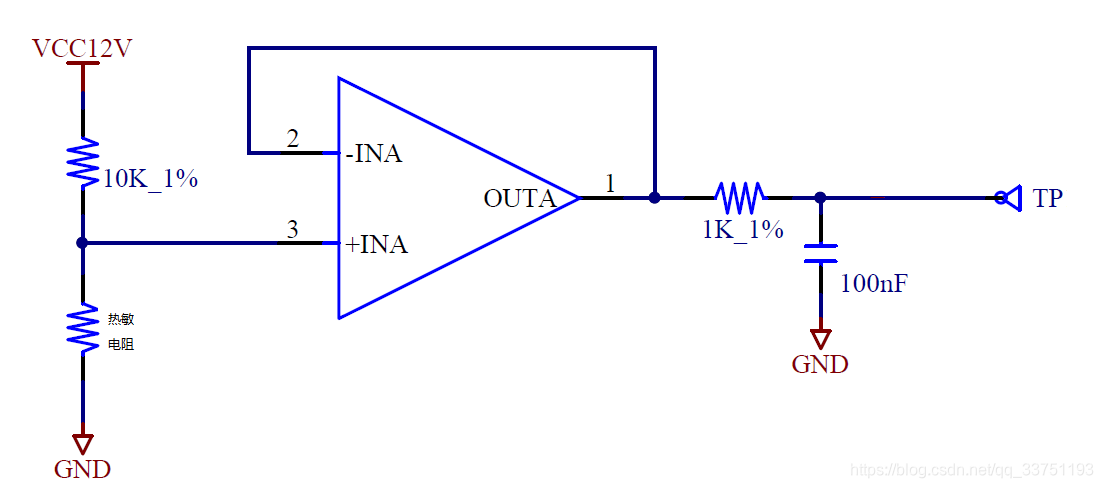
获取到电压值后，即可根据供电电压、采样到的电压，还有上拉的分压电阻的阻值三者的关系进行运算，即可获取到热敏电阻的阻值。
R_热敏 / ( R_热敏 + R_10K ) = V_TP / V_12V

拟合算法

1、使用多元拟合算法精确度难以达到要求，且对微控制器的运算负担较重。故不适用。
2、使用线性拟合算法运算量小，但由于温度跨度较大，无法获取准确拟合。
3、使用分段线性拟合算法，可克服以上两种算法所存在的问题。
以下内容为笔者运算分析的结果，目的在于分析分段线性拟合算法的准确度以及实际应用的可行性。

拟合算法是将所选温度节点两端的温度值以及对应的电阻值在笛卡尔坐标系中进行连线，形成二元一次函数。以25℃到30℃之间为例。如图是以25℃到30℃之间线性拟合后的结果，函数为：y = -0.3406 * x + 18.52。

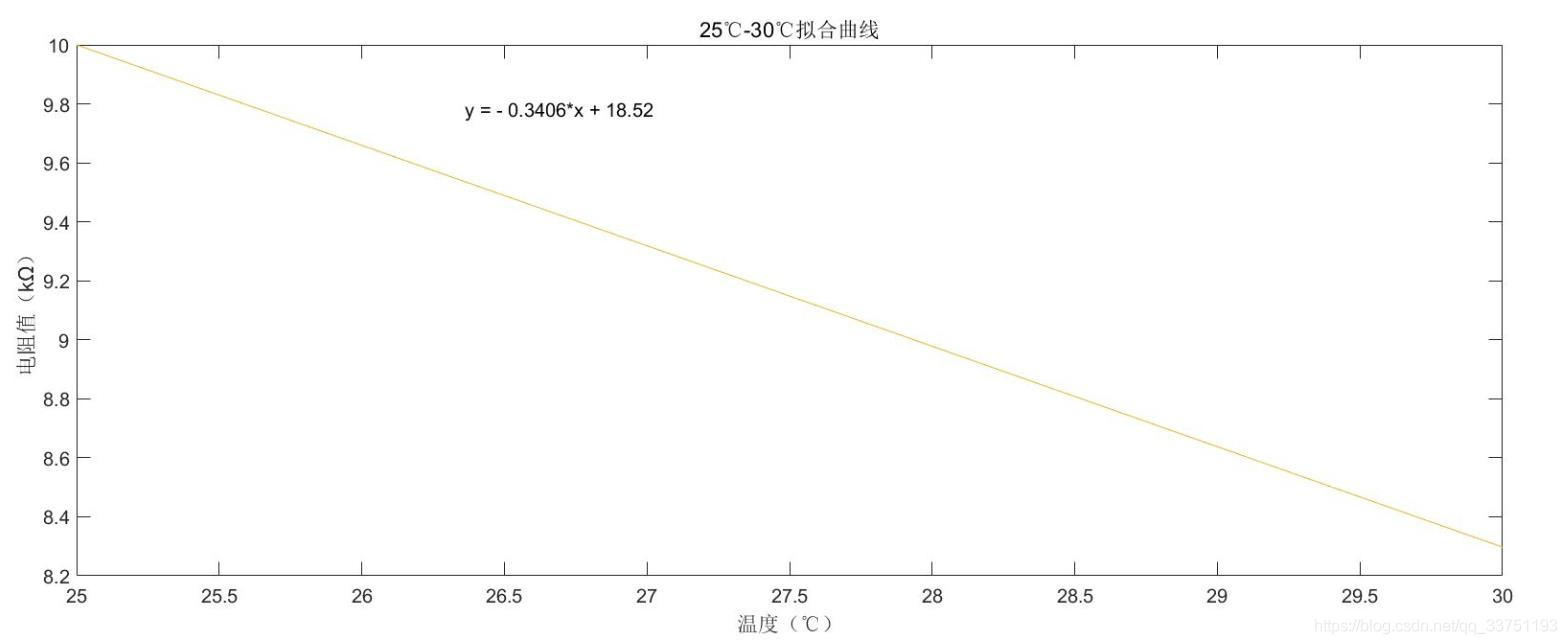
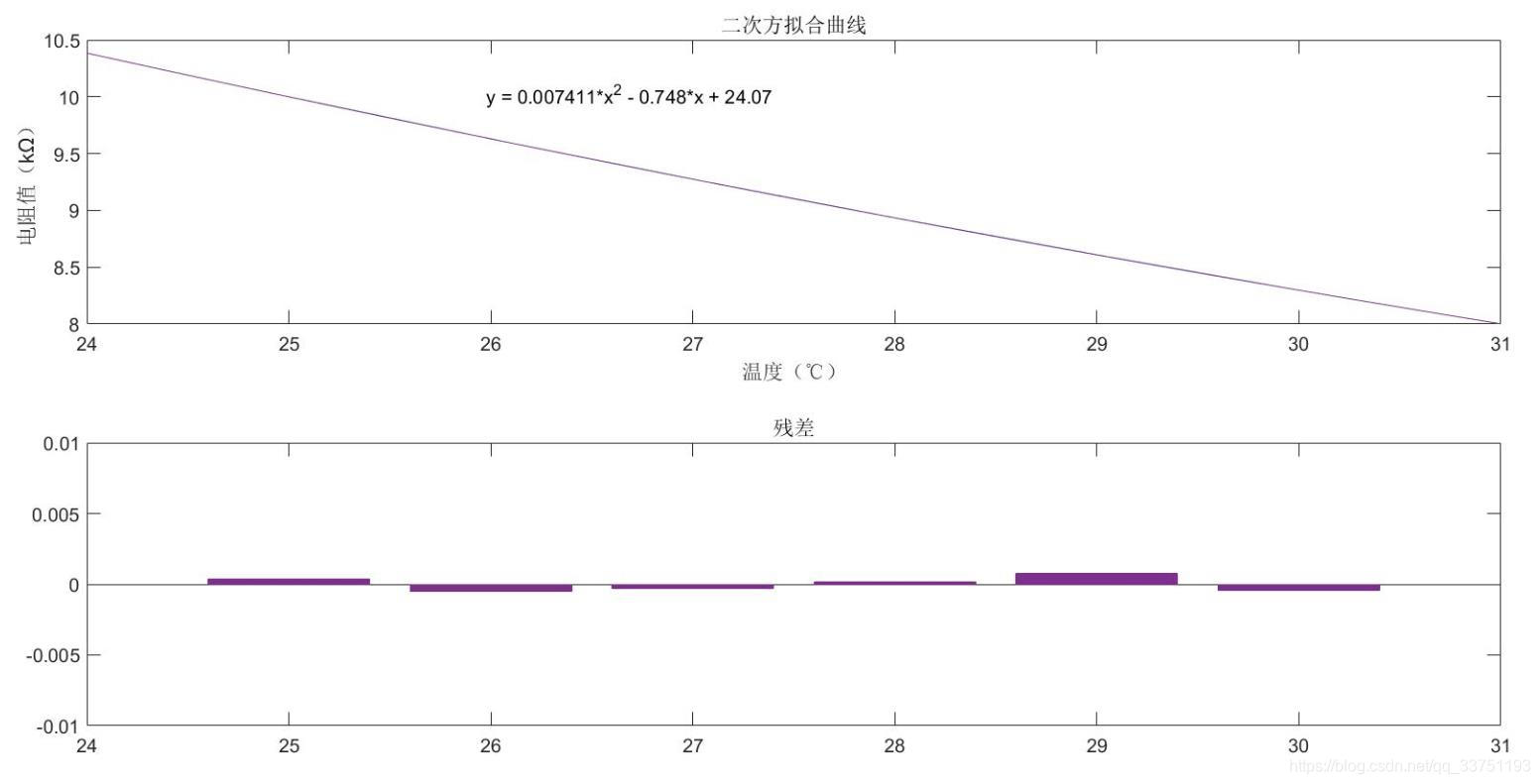
将25℃到30℃的源温度-电阻值曲线使用Matlab进行二次方拟合，可得如下图所示结果。由图可知，拟合结果为 y = 0.007411 * x^2 - 0.748 * x + 24.07，且残差小于0.005。即可认为已经完全等同于源曲线。

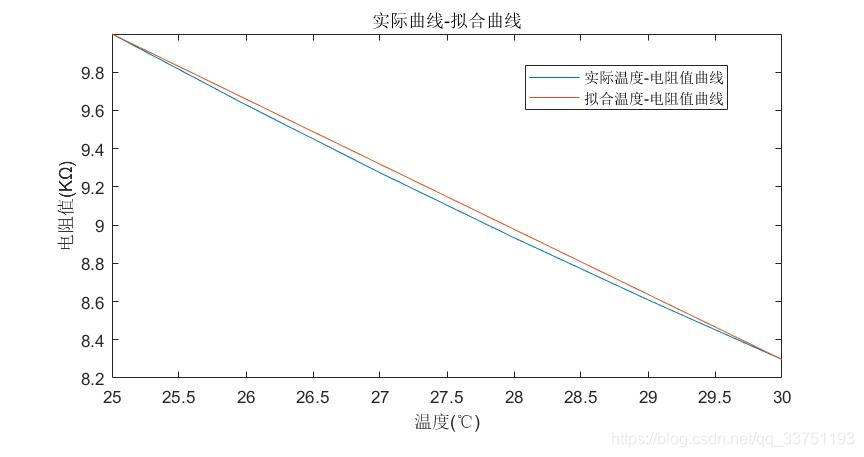
将25℃到30℃的实际曲线与线性拟合出来的直线重叠，可见二者是有一定误差的，且越靠近两个温度节点中心，误差越大。

以下找出误差最大的点的位置，
设二次方拟合曲线y1 = 0.007411 * x^2 - 0.748 * x + 24.07;
设线性拟合直线y2 = -0.3406 * x + 18.52;
令f(x) = y2-y1，x∈[25,30];
得f(x) = -0.007411x^2 + 0.4074x -5.57，x∈[25,30];
则f’(x) = -0.014822*x + 0.4074 = 0，x∈[25,30]时，即为函数f(x)的拐点，计算可得当x = 27.49 ≈ 27.5时，f’(x) = 0。
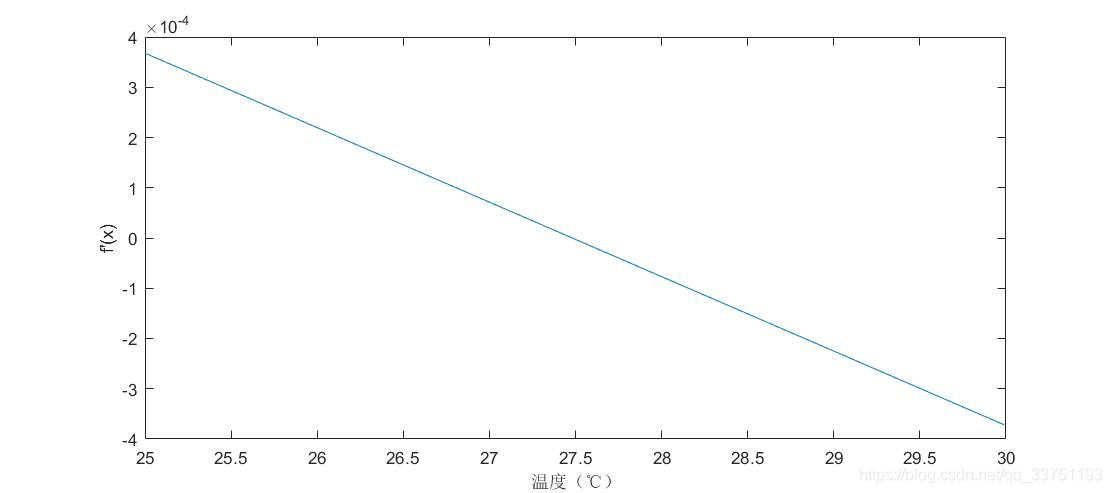
如图所示，当x∈[25,27.5)时，f’(x)＞0；当x∈(27.5,30]时，f’(x)＜0。即当当前温度位于两个取样点中间时，误差达到最大值。

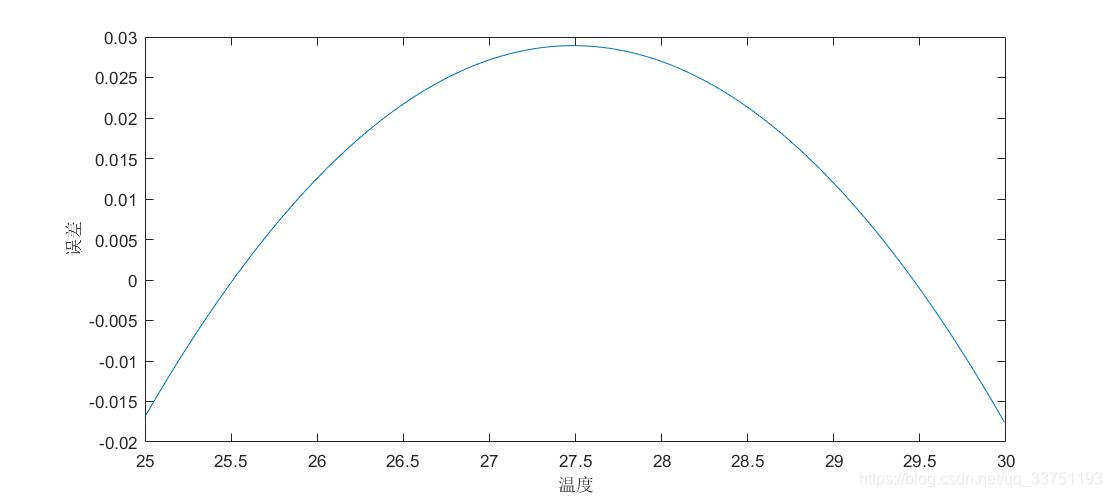
f(27.5) = 0.029。即当前温度为27.5℃时，计算出的电阻值与实际电阻值误差最大，为0.029kΩ。查表可知，由算法计算出的温度误差最大仅为+0.1℃，已经远小于热敏电阻本身因为制作工艺而导致的误差（±0.3℃）。

同理可推算出取温度节点间隔为10的情况，取[20,30]之间的数据进行运算。使用matlab拟合曲线后则可得：f’(x) = 0时，x = 24.95 ≈ 25；x∈[20,25)时，f’(x)＞0；当x∈(25,30]时，f’(x)＜0。即当当前温度位于两个取样点中间时，误差达到最大值。f(25) = 0.397kΩ，即当取样间隔为10℃时，最大计算误差不超过1℃。

分段拟合

以上说明了线性拟合算法在不同温度间隔下的拟合精度，可知在不考虑电阻本身设计误差的情况下，温度分割间隔为5℃时，误差最大不超过+0.1℃；在温度分割间隔为10℃的情况下，误差最大不超过+1℃。在不需要精确测量的温度区间，可使用10℃间隔进行运算，增加运算速度；在需要精确测量的温度区间，可使用5℃间隔进行运算，增加测量精度。
于是设计出以下算法，
1、首先将温度区间进行划分，在不需要精确测量的地方，使用10℃为一分割；在需要精确测量的地方，使用5℃为一分割。使用二维数组存储对应温度下的标准电阻值。
2、然后根据测量到的电压值进行运算，获取当前的电阻值（若需要更为精确地获取到实际温度，可用标准仪器与热敏电阻测出的实际温度做对比，将温度差值写进代码中，对使用的热敏电阻进行校准）。
3、在代码中进行扫描，判断热敏电阻的阻值所处的温度范围，然后在此区间中进行拟合运算，将获取到的热敏电阻阻值输入到拟合出来的函数中，即可获得当前的温度值。

#define SUPPORT_VOLTAGE     3.3f     //供电电压
#define REFERENCE_VOLTAGE   3.3f     //参考电压
#define DIVIDE              4096     //ADC位数
#define PULL_UP_RES         10       //上拉电阻
#define TEMP_NUM            19       //温度总共的档位数//第一行代表温度，分割档位可根据需要随意设置
//第二行代表相应的热敏电阻的阻值
const float temp_table[2][TEMP_NUM] = {{   -30,    -20,    -10,      0,      5,     10,     15,     20,    25,   30,    35,    40,    45,    50,    60,    70,    80,    90,   100},{122.0f, 72.04f, 44.09f, 27.86f, 22.39f, 18.13f, 14.77f, 12.12f, 10.0f, 8.3f, 6.92f, 5.81f, 4.89f, 4.14f, 3.01f, 2.23f, 1.67f, 1.27f, 0.98f}
};//根据二维数组表计算温度
int Temp_Cnt(int temp)
{float resist  = 0;  //电阻值float voltage = 0;  //电压值float k = 0;        //k值float b = 0;        //b值//计算电压值voltage = (float)temp / DIVIDE * REFERENCE_VOLTAGE;//电压限幅voltage = LIMIT(voltage,0,SUPPORT_VOLTAGE - 0.01f);//计算电阻值resist  = (PULL_UP_RES * voltage) / (SUPPORT_VOLTAGE - voltage);//数组之外的数据if(resist <= temp_table[1][TEMP_NUM - 1])     //电阻值小于最小值，返回值100度return (int)(1000);else if(resist >= temp_table[1][0])           //电阻值大于最大值，返回值-30度return (int)(-300);else{//遍历二维数组for(uint8_t i = 0; i < TEMP_NUM - 1; i++){//判定是否在计算范围内if(Isinside(resist,temp_table[1][i+1],temp_table[1][i])){//计算k值与b值k = (temp_table[0][i] - temp_table[0][i+1])/(temp_table[1][i] - temp_table[1][i+1]);b = temp_table[0][i] - k * temp_table[1][i];//计算出来的是温度与热敏电阻的二元一次函数的k值与b值break;}}//返回温度值return (int)((k * resist + b) * 10);}
}

算法使用二维数组存储温度节点对应的电阻值，可根据工程师需要直接修改二维数组即可，可根据实际情况，随意增加或减少温度节点的数量，无需改动算法。同时使用了自动线性插值算法，无需工程师手动计算函数，代码可根据二维数组的参数直接匹配运算。增加了可移植性与可拓展性。
当然也可在代码运行之后就根据二维数组直接运算出每一段的k和b，或由工程师直接运算出每一段的k和b，放入代码中，每次只需要匹配温度区间即可直接运算温度，无需每次都进行拟合。

谢谢阅读，有任何问题或新思路，均可沟通交流。
欢迎转载，转载请注明出处：https://blog.csdn.net/qq_33751193/article/details/115268541