嵌入式软件开发原理
嵌入式软件开发和我们传统的软件开发不一样。
就拿我们的QT开发,我们敲完代码之后直接编译运行exe看看效果,不行就改改再次编译运行,如果可以就打包exe文件相关的配置文件对吧,一套下来行云流水一气呵成。
但是我们编写STM32的运行程序的时候就会稍微麻烦一些,我们先敲代码,编译完之后拿着hex文件烧录进板子里,不行就改改再编译,再拿着新的hex文件烧录(Keil中可以进行仿真,但我不太会用,平时也不用,但是我们得知道是可以仿真调试的)。
因此在嵌入式软件开发中,我们一般是使用宿主机和目标机的模式进行系统开发,并且借助开发工具进行目标开发。
宿主机是PC机中构建的开发环境,目标机是嵌入式系统的实际运行环境或者是能够代替实际运行环境的仿真系统。
嵌入式软件开发方式一般是在宿主机上完成编码和交叉编译工作,与目标机建立连接之后将程序下载到目标机中进行交叉调试和运行。
交叉编译就是在一个平台生成在另一个平台上执行的代码。是因为我们的PC拥有非常丰富的系统资源,而嵌入式系统中的系统资源不足以支持我们进行直接的编译,因此我们常用的是交叉编译的方法。
在我们编译的时候,编译过程是这样的:词法分析,语法分析,语义分析,中间代码生成和代码优化。
最后还有一点要说的就是gdb,有时候软考刷题的时候会考到这个。
gdb是一个程序调试工具,主要功能有:执行程序,显示数据,断点,变量检查赋值,单步执行,函数调用等。
 根据上面说的gdb的功能,我们知道应该选择D,gdb无法帮我们检测代码中的语法错误。
根据上面说的gdb的功能,我们知道应该选择D,gdb无法帮我们检测代码中的语法错误。
C语言编程基础
C语言博大精深,我这说不明白,我就挑一点软考选择题中考的概率比较大的部分简单说一说。
C语言程序从main函数开始,以main函数结束结尾。
结构体(struct)占用的大小是所有成员大小的总和,联合体(union)的大小是所有成员中最大的那个的大小。
宏定义是直接替换掉原文的。我们来看看下面这段代码。
#define f1(x) x*x
#define f2(2) (x*x)int i = 100 / f1(10) ;
int j = 100 / f2(10) ;想一想 i 和 j 各是什么值。
。
。
。
i 是100,而 j 是1。
因为宏定义是直接替换原文的,因此替换完之后定义 i 和 j 的代码是变成下面这样的。
int i = 100 / 10*10 ;
int j = 100 / (10*10) ;在宏定义中加个括号,结果都会不一样,并且因为宏定义是直接替换原文的,因此一般宏定义中是不加分号的。
指针的大小就是当前机器的字长,比如说用的是8位单片机,那么不管这个指针指向什么类型的变量,它的大小都是8bit。如果是32位则是32bit。
使用指针来做函数的参数,是可以在函数内修改传入的指针指向的数据的值的。
数据结构与算法
数据结构与算法同样博大精深,无法速成,建议是去力扣刷几道题,自然而然就明白了。推荐刷一下LeetCode75这个专题的题目,在公众号之前的文章中有文章讲解,我b站同名账号有相应的算法题讲解视频。
这边就稍微提一提软考高频考点。
线性表
线性表按照存储方式可以分为顺序表和链表。
顺序表需要一段连续的内存空间来存放,因此表中相邻的元素在物理地址上也是相邻的,C语言中的数组就是顺序表,有时候会让我们计算数组中某元素的物理地址,我们就根据这个原理来计算的,不过计算的时候要看清楚数组存放是按行排的还是按列排的。

链表就比较随意了,因为它们是靠指针来连接的,所以在物理空间中不必相邻。

从上面二者结构上的差异我们也可以看得出,顺序表中要插入、删除数据的比较麻烦的,需要移动相邻的元素,而线性表只需要修改元素中的前序指针和后序指针即可。
但是在查找数据上看,顺序表显然更快,因为它的元素都是连在一起的,而链表的元素可以分布得很零散,不好找。
队列和栈
队列就是先进先出。
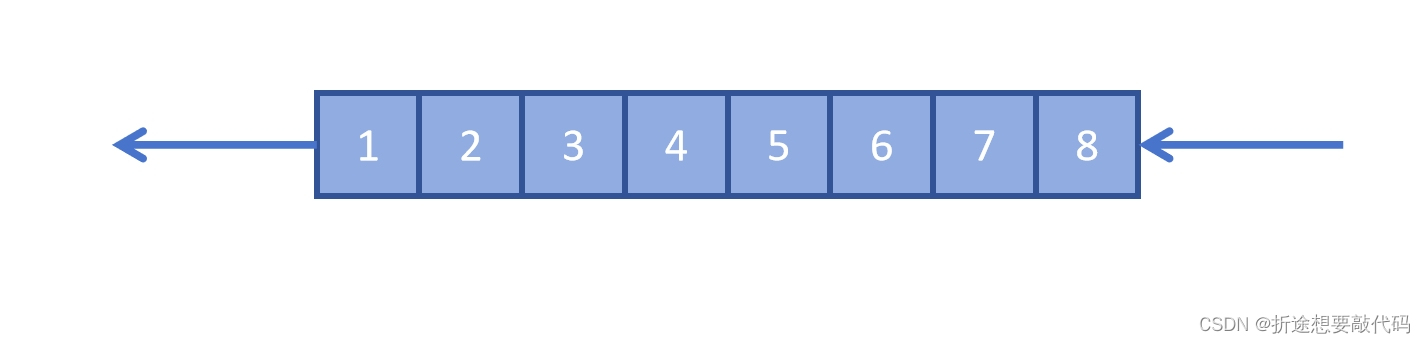
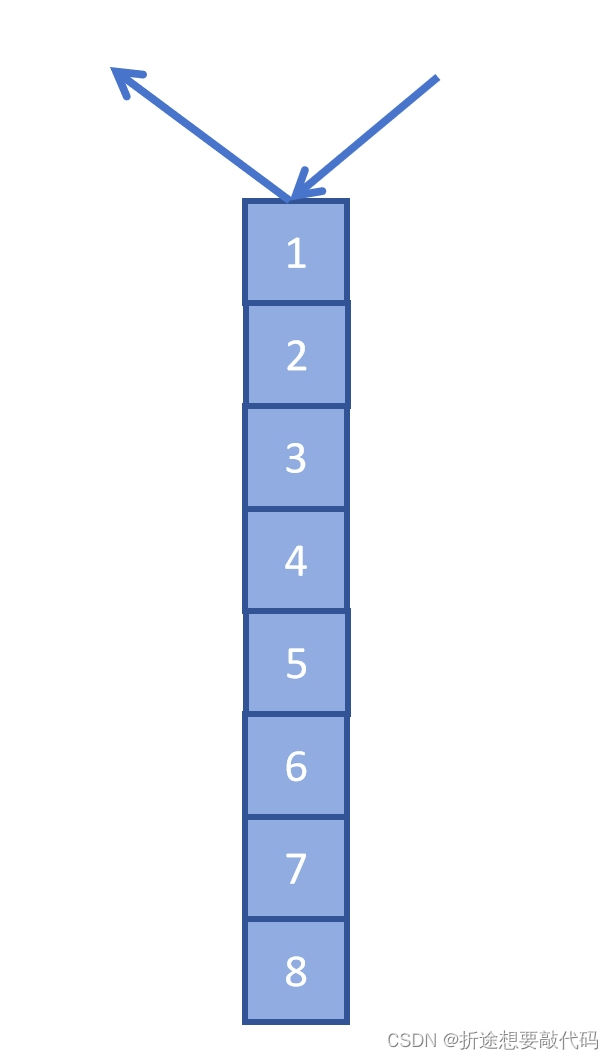
栈就是先进后出,也就是越后面进的,出的越早。
树
树只有两种,一种是二叉树,另一种不是二叉树。
每个节点最多只有两个子树的就是二叉树。
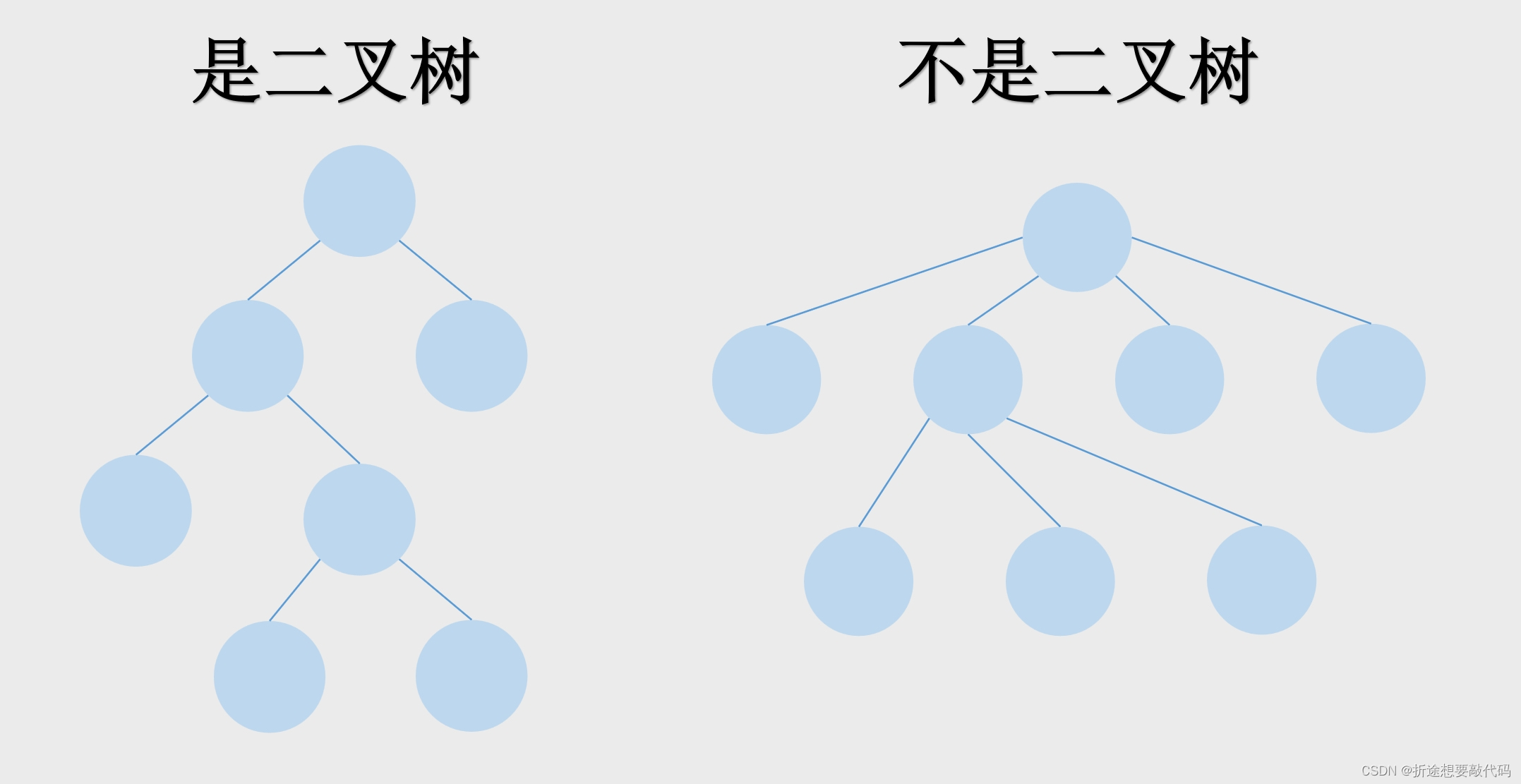
常见的树都是二叉树,不过二叉树也分为很多种。
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。并且满二叉树的叶子节点数是2^(k-1)。
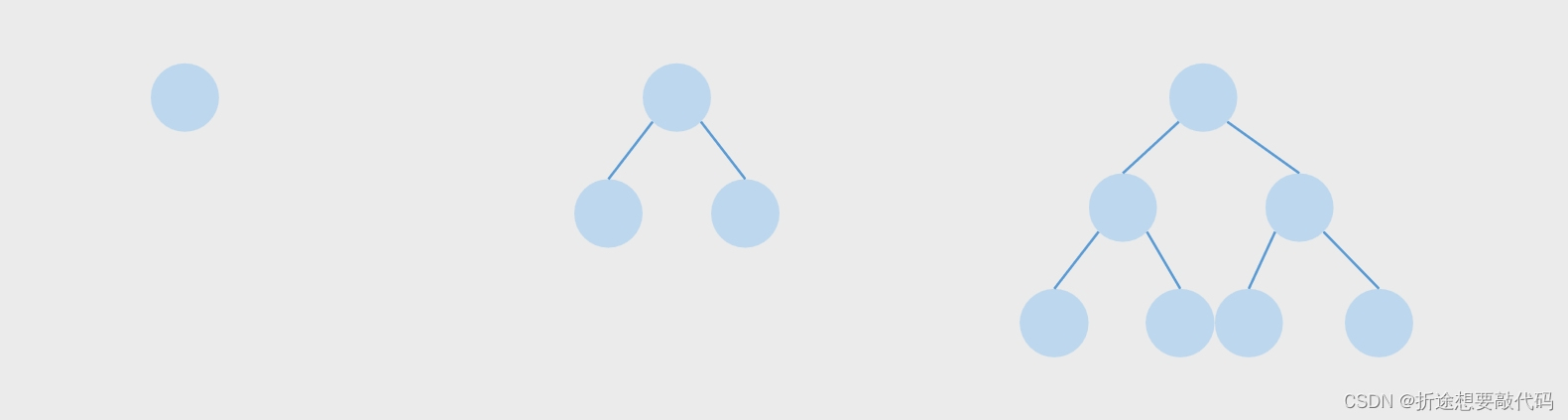
若设二叉树的深度为k,除第k层外,其它各层 (1~k-1) 的结点数都达到最大个数(即1~k-1层为一个满二叉树),第k层所有的结点都连续集中在最左边,这就是完全二叉树。
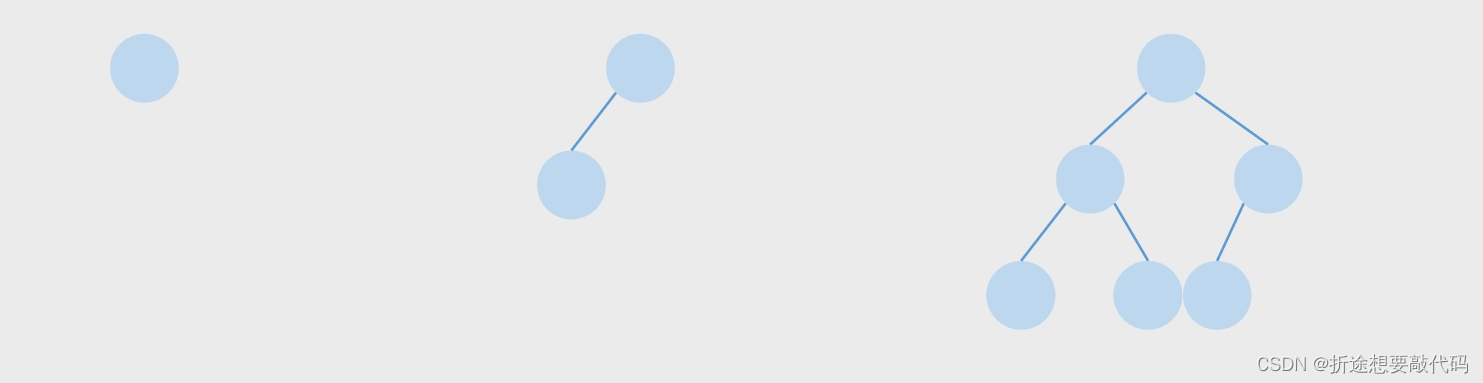
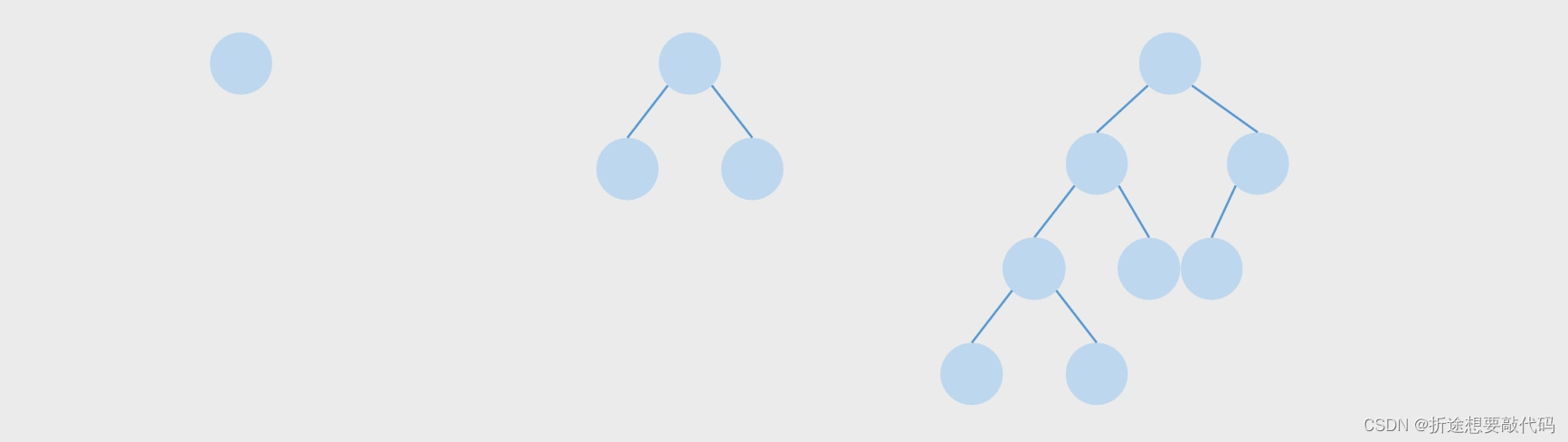
平衡二叉树要么是一棵空树,要么保证左右子树的高度之差不大于 1,并且子树也必须是一棵平衡二叉树。
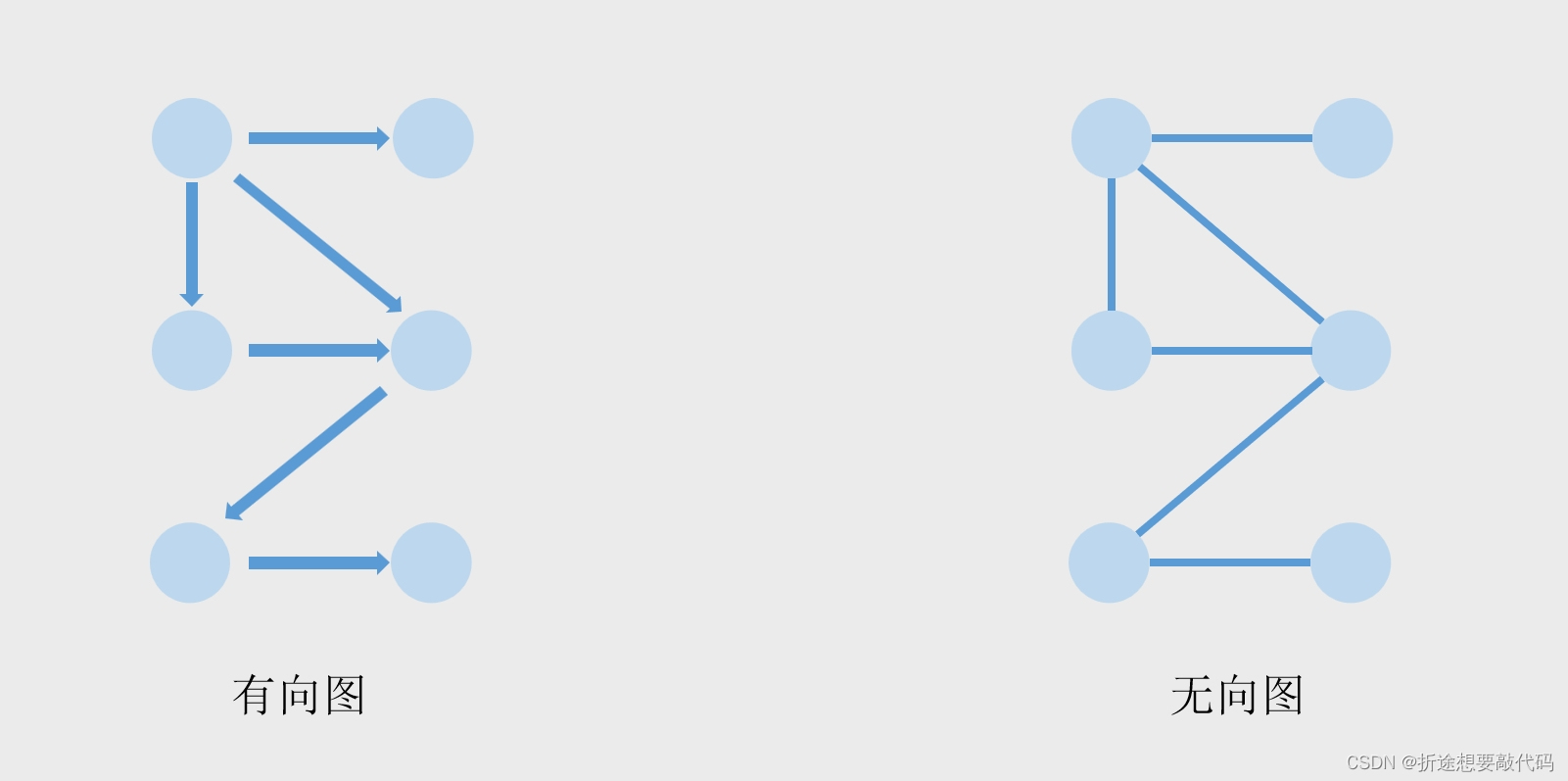
图
图也分为两种,有向图和无向图,有箭头指向的就是有向图,没有箭头的就是无向图。
图中每个节点都有一些属性,比如说度,度又分为出度和入度,每有一个箭头指向该节点,那么这个节点的入度+1,每有一个箭头从该节点指出,那么该节点的出度+1。
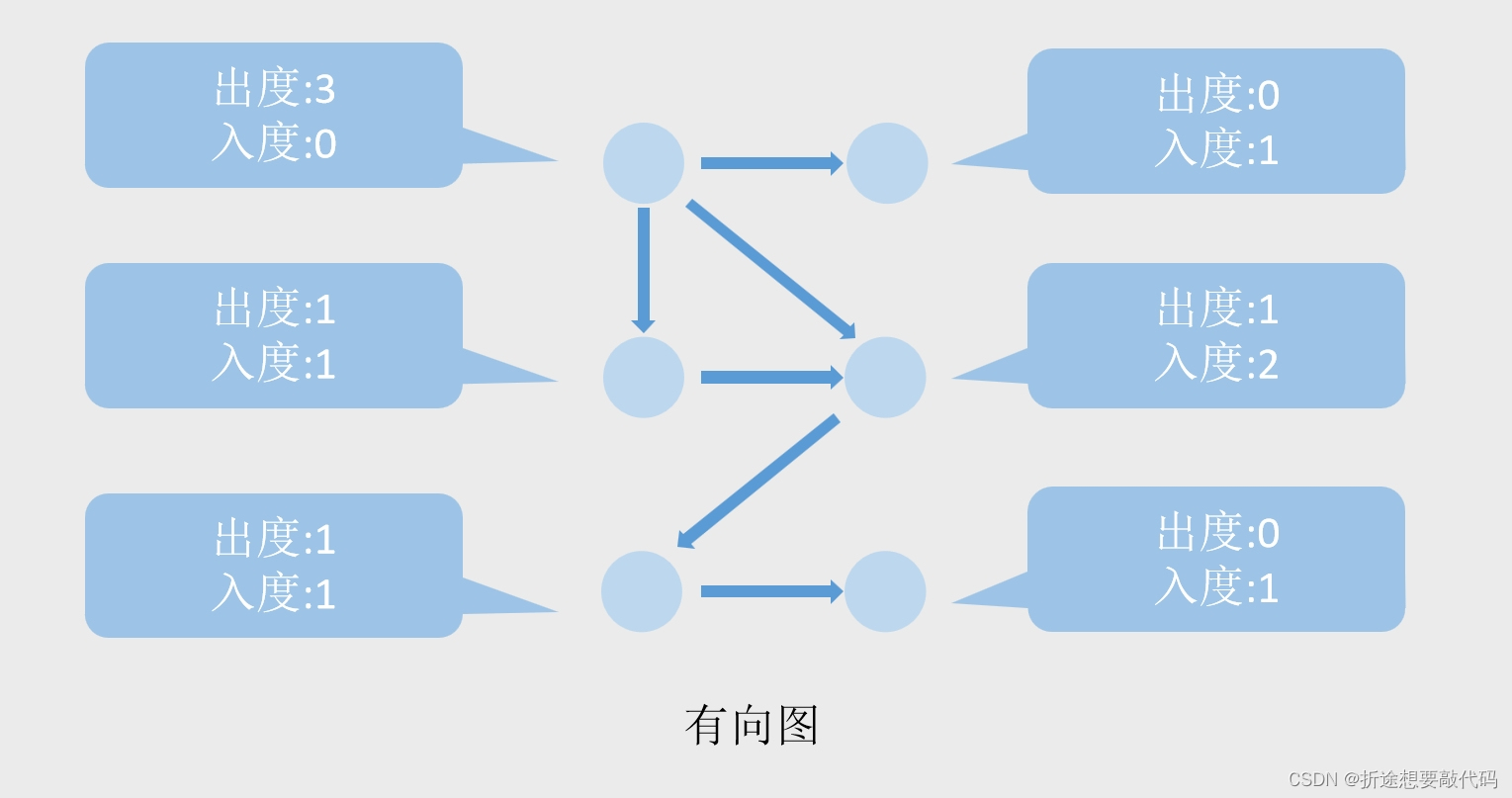
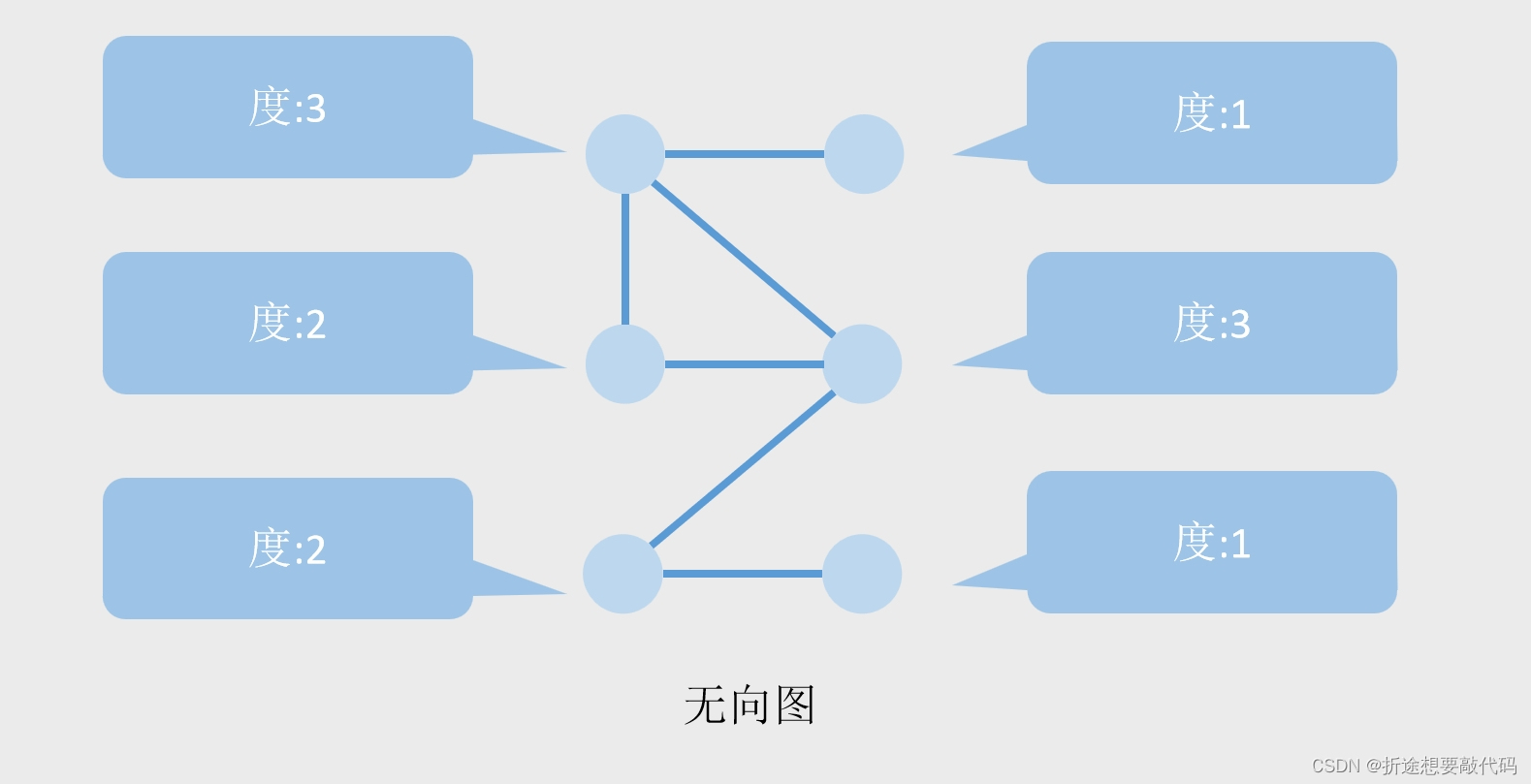
但是无向图没有箭头,也就没有出度入度,取而代之的就是单纯的度,每有一根线连着节点,那么该节点的度+1。
算法复杂度
算法复杂度分为时间复杂度和空间复杂度。
时间复杂度是指执行算法所需的计算工作量,空间复杂度是指执行算法所需要的内存空间。
如何计算这个东西,我也说不太明白,就是凭感觉选出来的(你们不要学我),我们让文心一言来解答一下。
时间复杂度
时间复杂度通常用大O表示法(Big O notation)来描述。大O表示法关注的是算法执行时间随输入规模增长的上限。
要计算时间复杂度,你需要考虑算法中各个基本操作的执行次数,并找出这些次数与输入规模(如数组的大小、列表的长度等)之间的关系。以下是一些常见的时间复杂度示例:
- O(1):算法的执行时间不随输入规模的增长而增长,即常量时间复杂度。
- O(n):算法的执行时间与输入规模成线性关系。
- O(n^2):算法的执行时间与输入规模的平方成正比。
- O(log n):算法的执行时间与输入规模的对数成正比。
- O(n log n):算法的执行时间同时受到输入规模的线性对数影响。
为了计算时间复杂度,你需要:
- 找出算法中的基本操作(如赋值、比较、循环等)。
- 计算每个基本操作在算法执行过程中被执行的次数。
- 用输入规模(如n)来表示这些次数。
- 找出次数随输入规模增长的主要项(通常忽略常数系数和低阶项)。
- 用大O表示法来表示这个主要项。
空间复杂度
空间复杂度同样可以用大O表示法来描述。它关注的是算法执行过程中所需额外空间随输入规模增长的趋势。
要计算空间复杂度,你需要考虑算法在执行过程中除了输入数据外还需要使用多少额外的存储空间。这包括变量、数组、链表、栈、队列等数据结构所占用的空间。以下是一些常见的空间复杂度示例:
- O(1):算法所需的额外空间不随输入规模的增长而增长,即常量空间复杂度。
- O(n):算法所需的额外空间与输入规模成线性关系。
为了计算空间复杂度,你需要:
- 找出算法执行过程中所使用的所有额外数据结构。
- 计算每个数据结构所需的存储空间。
- 用输入规模(如n)来表示这些存储空间。
- 找出存储空间随输入规模增长的主要项(同样忽略常数系数和低阶项)。
- 用大O表示法来表示这个主要项。
注意:在计算空间复杂度时,通常只考虑算法在执行过程中所需的额外空间,而不包括输入数据本身所占用的空间。