二叉树的遍历

二叉树遍历大体上分为深度优先遍历（DFS)和宽度优先遍历(BFS)：

深度优先遍历(DFS)

对于深度优先遍历，又可以分为前序、中序和后序遍历，对于一个二叉树，无非包括三个部分根节点、左子树和右子树，其子树也是相同组成方式。顾名思义，二叉树的前中后序遍历就是表示什么时候遍历该二叉树的根节点（包括其子树），例如对于前序遍历而言，我们先遍历根节点然后在遍历左子树，最后再遍历右子树。各个遍历方式如下所示：

前序遍历次序：根–>左子树–>右子树
中序遍历次序：左子树–>根–>右子树
后续遍历次序：左子树–>右子树–>根

对于如下所示的树：

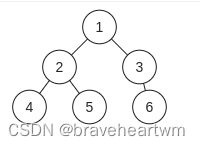
前序遍历：1,2,4,5,3,6
中序遍历：4,2,5,1,3,6
后续遍历：4,5,2,6,3,1

可以验证上述理论，对于子树也相同适用。

递归遍历

如何实现上述遍历呢，我们很容易想到递归方式，例如对于前序遍历，我们先遍历根节点，然后分别递归遍历左子树右子树。代码实现也很简单：

// 前序遍历就是在递归前处理根节点数据,这里打印数据
std::cout << root->val << std::endl;
preorderTraversal(root->left);
preorderTraversal(root->right);

同样的对于中序和后序：

inorderTraversal(root->left);
// 中序遍历就是在递归中间处理根节点数据,这里打印数据
std::cout << root->val << std::endl;
inorderTraversal(root->right);

postorderTraversal(root->left);
postorderTraversal(root->right);
// 后序遍历就是在递归后处理根节点数据,这里打印数据
std::cout << root->val << std::endl;

具体代码如下：

前序递归遍历：

class Solution {vector<int> preorderTraversal(TreeNode *root) {vector<int> res;preorderTraversal(root, res);return res;}void preorderTraversal(TreeNode *root, vector<int> &res) {if (!root) {return;}res.push_back(root->val);preorderTraversal(root->left, res);preorderTraversal(root->right, res);}
};

中序递归遍历

class Solution {public:vector<int> inorderTraversal(TreeNode *root) {vector<int> res;inorderTraversal(root, res);return res;}void inorderTraversal(TreeNode *root, vector<int> &res) {if (!root) {return;}inorderTraversal(root->left, res);res.push_back(root->val);inorderTraversal(root->right, res);}
};

后续递归遍历

class Solution {public:vector<int> postorderTraversal(TreeNode *root) {vector<int> res;postorderTraversal(root, res);return res;}void postorderTraversal(TreeNode *root, vector<int> &res) {if (!root) {return;}postorderTraversal(root->left, res);postorderTraversal(root->right, res);res.push_back(root->val);}
};

非递归遍历

对于非递归遍历，我们可以从递归展开中获得灵感，对于递归，如果没有到底部，之前的所有数据会一直执行压栈，只是在压栈过程中何时遍历根节点的问题。直接看代码：

前序非递归遍历

class Solution {public:vector<int> preorderTraversal(TreeNode *root) {vector<int> res;stack<TreeNode *> q;while (!q.empty() || root) {if (root) {// 在压栈前遍历根节点res.push_back(root->val);q.push(root);root = root->left;} else {root = q.top();q.pop();root = root->right;}}return res;}
};

中序非递归遍历

class Solution {public:vector<int> inorderTraversal(TreeNode *root) {vector<int> res;stack<TreeNode *> q;while (!q.empty() || root) {if (root) {q.push(root);root = root->left;} else {root = q.top();q.pop();// 在处理右子树之前遍历res.push_back(root->val);root = root->right;}}return res;}
};

后续非递归遍历

后续遍历稍微复杂一点，这里采用先遍历：根–>右子树–>左子树的方式，然后将其结果逆序就变成了：左子树–>右子树–>根 的方式，不过逆序也可以用栈来实现

class Solution {public:vector<int> postorderTraversal(TreeNode *root) {vector<int> res;stack<TreeNode *> s1;while (!s1.empty() || root) {if (root) {res.push_back(root->val);s1.push(root);// 先遍历右子树root = root->right; } else {root = s1.top();s1.pop();root = root->left;}}reverse(res.begin(), res.end());return res;
};

宽度优先遍历（BFS):

宽度优先遍历根据队列的方式遍历，vector中的vector为每层中遍历结果。

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> q;vector<vector<int>> res;if (!root) {return res;}q.push(root);while(!q.empty()) {vector<int> tmp;int size = q.size();while(size > 0) {TreeNode* node = q.front();q.pop();tmp.push_back(node->val);if (node->left){q.push(node->left);}if (node->right) {q.push(node->right);}size--;}res.push_back(tmp);}return res;}
};