本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：算法从入门到精通
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目一解析

给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。
对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。
如果数组中不存在该元素，则返回“-1 -1”。

输入格式
第一行包含整数n和q，表示数组长度和询问个数。
第二行包含n个整数（均在1~10000范围内），表示完整数组。
接下来q行，每行包含一个整数k，表示一个询问元素。
输出格式
共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。
如果数组中不存在该元素，则返回“-1 -1”。
数据范围
1≤n≤100000
1≤n≤100000

1≤q≤10000
1≤q≤10000

1≤k≤10000
1≤k≤10000

样例
输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1

算法原理

本题是练习二分很好的一道题目，二分程序虽然简单，但是如果写之前不考虑好想要查找的是什么，十有八九会是死循环或者查找错误，就算侥幸写对了也只是运气好而已。

用二分去查找元素要求数组的有序性或者拥有类似于有序的性质，对本题而言，一个包含重复元素的有序序列，要求输出某元素出现的起始位置和终止位置，翻译一下就是：在数组中查找某元素，找不到就输出−1
找到了就输出不小于该元素的最小位置和不大于该元素的最大位置。所以，需要写两个二分，一个需要找到>=x的第一个数，另一个需要找到<=x的最后一个数。查找不小于x的第一个位置，较为简单：

int l = 0, r = n - 1;
while (l < r) {int mid = l + r >> 1;if (a[mid] < x)  l = mid + 1;else    r = mid;
}

当a[mid]<x时，令l=mid+1，mid及其左边的位置被排除了，可能出现解的位置是mid+1及其后面的位置。

当a[mid]>=x时，说明mid及其左边可能含有值为x的元素。

当查找结束时，l与r相遇，l所在元素若是x则一定是x出现最小位置，因为l左边的元素必然都小于x。

查找不大于x的最后一个位置，便不容易了：

int l1 = l, r1 = n;
while (l1 + 1 < r1) {int mid = l1 + r1 >> 1;if (a[mid] <= x)  l1 = mid;else    r1 = mid;
}

要查找不大于x的最后一个位置：
当a[mid]<=x时，待查找元素只可能在mid及其后面，所以l=mid；
当a[mid]>x时，待查找元素只会在mid左边，令r=mid。

int l = 0, r = n - 1;
while (l < r){int mid = l + r + 1 >> 1;if (a[mid] <= x) l = mid;else r = mid - 1;}

int l1 = l, r1 = n - 1;
while (l1 < r1) {int mid = l1 + r1 >> 1;if (a[mid] <= x)  l1 = mid + 1;else    r1 = mid - 1;
}
printf("%d %d\n", l, l1 - (a[l1] == x ? 0 : 1));

代码实现

#include <iostream>
using namespace std;
const int maxn = 100005;
int n, q, x, a[maxn];
int main() 
{cin>>n>>q;for (int i = 0; i < n; i++)cin>>a[i];while (q--) {scanf("%d", &x);int l = 0, r = n - 1;while (l < r) {int mid = l + r >> 1;if (a[mid] < x)  l = mid + 1;else    r = mid;}if (a[l] != x){printf("-1 -1\n");continue;}int l1 = l, r1 = n;while (l1 + 1 < r1) {int mid = l1 + r1 >> 1;if (a[mid] <= x)  l1 = mid;else    r1 = mid;}cout<<l<<" "<<l1<<endl;}return 0;
}

题目二解析

给定一个浮点数 n，求它的三次方根。

输入格式
共一行，包含一个浮点数 n。

输出格式
共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围
−10000≤n≤10000
输入样例：
1000.00
输出样例：
10.000000

算法原理

这道题是一个浮点二分的题目

代码实现

#include <iostream>
#include <cstdio>
using namespace std;
double x;
int main() 
{cin >> x;// 确定边界值double l = -100000, r = 100000;// 注意循环条件处理精度问题while (r - l > 1e-8) {// 步骤 A: 找中间值double mid = (l + r) / 2;// 步骤 B: 判断if (mid * mid * mid < x) l = mid;else r = mid;}printf("%.6f", r);return 0;
}

题目三解析

输入一个长度为 n 的整数序列。

接下来再输入 m个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l个数到第 r个数的和。

输入格式
第一行包含两个整数 n和 m。

第二行包含 n个整数，表示整数数列。

接下来 m行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式
共 m行，每行输出一个询问的结果。

数据范围
1 ≤l ≤ r ≤ n,
1 ≤ n,m ≤ 100000,
−1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10

算法原理

本题用到了前缀和的知识：
什么是前缀和？
数列的和时，Sn = a1+a2+a3+…an; Sn就是数列的前 n 项和。
前缀和就是新建一个数组，新建数组中保存原数组前 n 项的和。

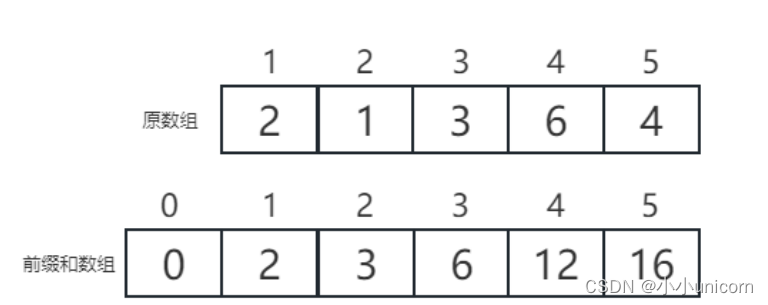
前缀和有什么用？
快速求某个区间中所有元素的加和。
例 S4 = a1 + a2 + a3 + a4; S1 = a1。所以可以通过 S4-S1 得到 a2+a3+a4 的值。

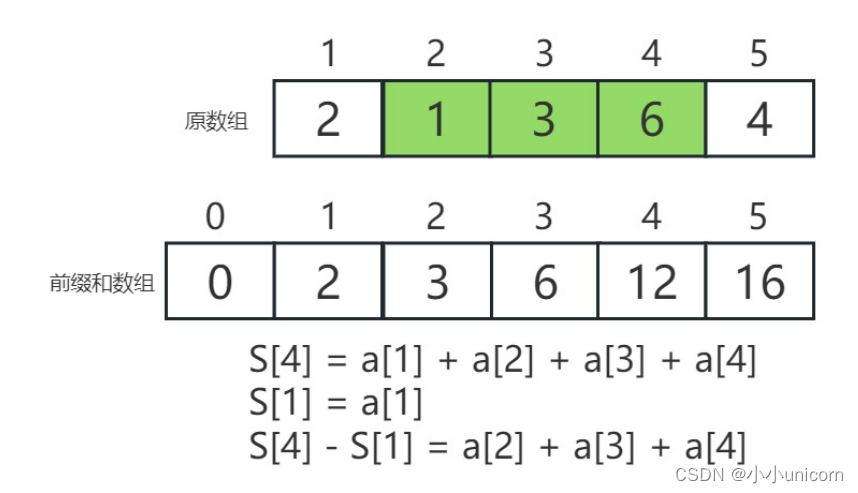
代码实现

#include <iostream>
using namespace std;
const int N = 100010;
int a[N];//保存原数组
int s[N];//保存前缀和
int main()
{int n, m;cin >> n >> m;//从a[1]开始保存。a[0]是0for(int i = 1; i <= n; ++i){cin >> a[i];}s[0] = 0;//计算前缀和for(int i = 1; i <= n; ++i)s[i] = s[i - 1] + a[i];for(int i = 0; i < m; ++i){int l, r;//保存区间cin >> l >> r;//s[r] = a[1]+ ··· + a[r]//s[l - 1] = a[1]+ ··· + a[l - 1]//s[r] - s[l - 1] = a[l] + ··· + a[r]cout << s[r] - s[l - 1] << endl;}
}

题目四解析

输入一个 n 行 m列的整数矩阵，再输入 q个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q
。
接下来 n行，每行包含 m个整数，表示整数矩阵。
接下来 q行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

算法原理

一步一步学会二维前缀和的推导
给出一个二维数组，在给出一个子数组的左上角坐标、右下角坐标，求出子数组中的所有元素的和。

用s[i,j]表示(1,1)~(i,j)的和。

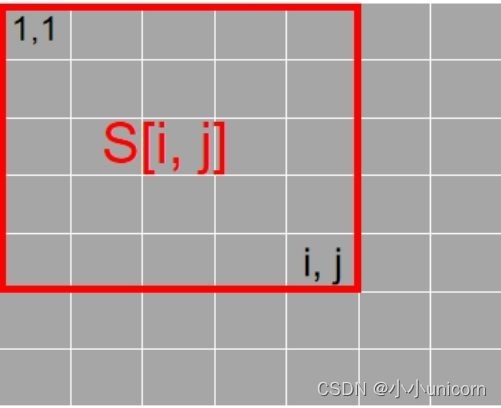
先看看s[i,j]怎么求：

s[1,1] = a[1,1]s[1,2] = a[1,1] + a[1,2]= s[1,1] + a[1,2]s[1,3] = a[1,1] + a[1,2] + a[1,3] = s[1,2] + a[1,3] s[2,1] = a[1,1] + a[2,1] = s[1,1] + a[2,1] s[2,2] = a[1,1] + a[1,2] + a[2,1] +  a[2,2] = s[1,2] + s[2,1] - s[1,1] + a[2, 3] s[2,3] = a[1,1] + a[1,2] + a[1,3] + a[2,1] + a[2,2] + a[2,3] = s[1,3] + s[2,2] - s[1,2] + a[2, 3] 

可以得到一下公式：
s[i,j] = s[ i−1,j ]+ s [ i , j−1 ] - s[ i−1, j−1 ]+ a[ i ][ j ]
也就是，可以在o(n²)的时间复杂度内求出所有s
当求出 s，求 (x1,y1)~(x2,y2)的和

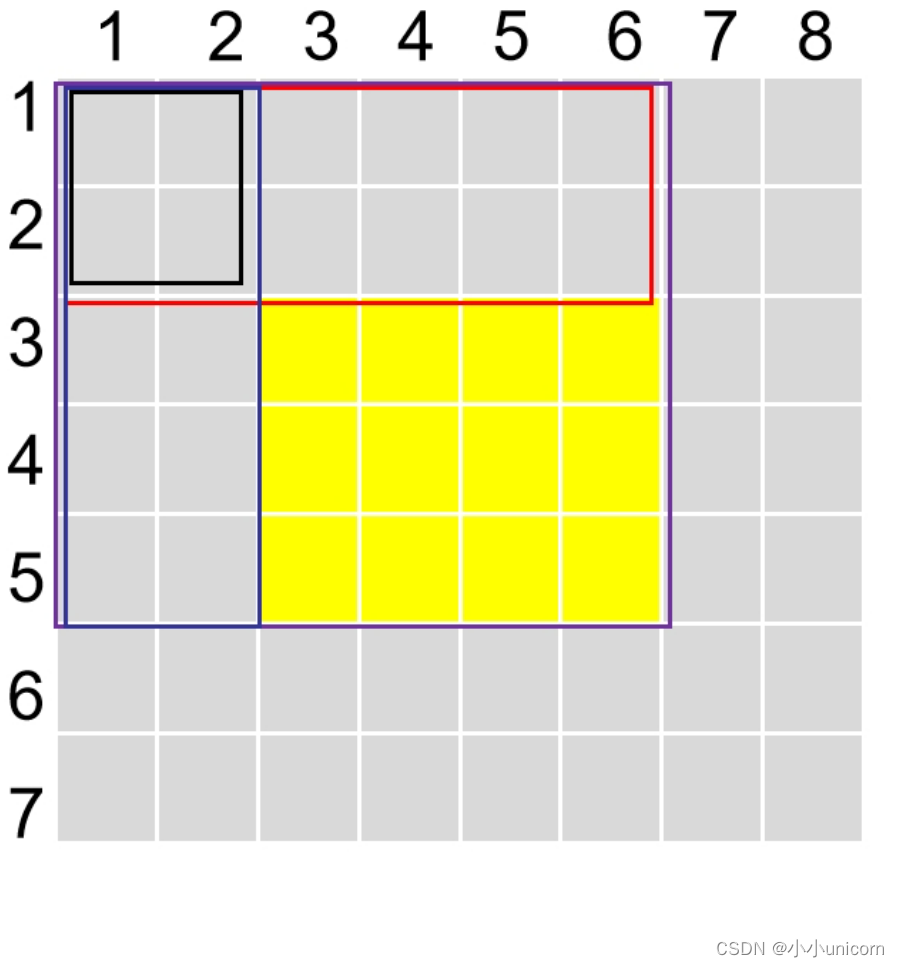
如图所示：黄色部分 = 紫色框 - 蓝色框 - 红色框 + 黑色框。

也就是：

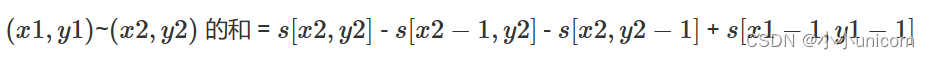
所以当求出 s 后，就能在 o(1)的时间复杂度内，求出子矩阵的和。

所以总时间复杂度是：o(n²)

#include <iostream>
using namespace std;const int N = 1010;
int a[N][N];
int s[N][N];int m, n, q;
int main(){cin >> n >> m >> q;for(int i = 1; i <= n; i++){for(int j = 1; j <=m; j++){cin >> a[i][j];}}// 求 s[i, j]for(int i = 1; i <= n; i++){for(int j = 1; j <=m; j++){s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];}}while(q > 0){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;// 求子矩阵和cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;q --;}
}

题目五解析

算法原理

算法一(贪心)
题意：就是要我们找到最小值让机器人可以达到终点
我们先看一组样例：3 4 3 2 4
要想它最小，我们可以直接从最后面开始运算，初始化他的代价为0，我们设初值为x

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int num[N];
int n;
int main()
{cin>>n;for(int i=0;i<n;i++)cin>>num[i];int res = 0;for(int i = n - 1; i >= 0; i--){if((num[i] + res) % 2 == 0)res = (num[i] + res) / 2;elseres = (num[i] + res) / 2 + 1;}cout<<res<<endl;
}

算法二：容器

#include<bits/stdc++.h>
using namespace std;
int main() 
{int n;cin >> n;vector<int> v(n);for (int i = 0; i < n; ++i)cin >> v[i];int res = 0;for (int i = n-1; i >= 0; i--) {if((v[i] + res) % 2 == 0)res = (v[i] + res) / 2;elseres = (v[i] + res) / 2 + 1;}cout << res << endl;return 0;
}

题目六解析

四平方和定理，又称为拉格朗日定理：

每个正整数都可以表示为至多 4个正整数的平方和。

如果把 0包括进去，就正好可以表示为 4个数的平方和。

比如：

5=0²+0²+1²+2²

7=1²+1²+1²+2²
对于一个给定的正整数，可能存在多种平方和的表示法。

要求你对 4个数排序：
0 ≤ a ≤ b ≤ c ≤ d
并对所有的可能表示法按 a,b,c,d为联合主键升序排列，最后输出第一个表示法。

输入格式
输入一个正整数 N。

输出格式
输出4个非负整数，按从小到大排序，中间用空格分开。

数据范围
0<N<5∗106
输入样例：
5
输出样例：
0 0 1 2

算法原理

根据题意，直接四重循环暴力枚举a,b,c,d，意料之中的超时了，后来慢慢优化，优化成三重循环，仍然不行(当时没有理解清楚到 a <= b<= c<= d这个关系)，再然后,就想到了打表

1. 建立哈希表，存储小于n的数c,假设e = c^2 + d^2,则h[e] = c,从小到大遍历c, d只存储先出现的(因为字典序小)
2. 从小到大遍历a、b,查找1中建立的哈希表,若 h[n - a^2 - b^2]存在,则算出d,

代码实现

#include<iostream>
#include<cmath>
using namespace std;
const int N = 1e8 + 10;
int h[N];
int main() 
{int n;cin >> n;//打表，找出1 - n，所有完全平方数两两之和，如果存在只记第一次出现（题目要求找出字典序小的）for (int i = 0; i * i * 2<= n; i++) {for (int j = i; j * j + i * i <= n; j++) {if (!h[i * i + j * j])h[i * i + j * j] = i + 1;//防止i = 0时在后面判断查找跳过 i = 0的情况}}//0<= a <= b <= c <= d,可以得出a^2 <= n / 4, a^2 + b^ 2 <= n / 2; for (int i = 0; i * i * 4 <= n; i++) {for (int j = i; j * j + i * i <= n / 2; j++) {int t = n - i * i - j * j;if (h[t]) {int c = h[t] - 1;   //防止开根号后因为精度关系,向下取整,例:25 开根号得到4.99999向下取整为4;int d = (sqrt(t - c * c) + 1e-4);printf("%d %d %d %d", i, j, c, d);return 0;}}}return 0;
}

题目七解析

儿童节那天有 K 位小朋友到小明家做客。

小明拿出了珍藏的巧克力招待小朋友们。

小明一共有 N块巧克力，其中第 i块是 H_i×W_i的方格组成的长方形。

为了公平起见，小明需要从这 N块巧克力中切出 K块巧克力分给小朋友们。

切出的巧克力需要满足：

形状是正方形，边长是整数大小相同
例如一块 6×5的巧克力可以切出 6
块 2×2 的巧克力或者 2块 3×3的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式
第一行包含两个整数 N和 K。

以下 N行每行包含两个整数 Hi和 Wi。

输入保证每位小朋友至少能获得一块 1×1
的巧克力。

输出格式
输出切出的正方形巧克力最大可能的边长。

数据范围
1≤N,K≤10⁵,
1≤H_i,W_i≤10⁵
输入样例：
2 10
6 5
5 6
输出样例：
2

算法原理

思路：

小巧克力边长 a 一定在 1 – 100000 之间

答案即为：在 1 – 100000 之间找到一个最大的数，使得所有的 (w[i]/a) * (h[i]/a) 之和大于要求的数量 k。

使用二分法找到 a 的最大取值即为答案。

代码实现

#include <iostream>
using namespace std;int const N = 100010;
int w[N], h[N];//存储长、宽
int n, k;bool chack(int a)
{int num = 0;//记录分成长度为 a 的巧克力数量for (int i = 0; i < n; i++){num += (w[i] / a) * (h[i] / a);//每一大块可以分成的边长为 a 的巧克力数量if (num >= k) return true;//大于要求数量，返回真}return false;
}int main()
{cin >> n >> k;for (int i = 0; i < n; i++) cin >> h[i] >> w[i];int l = 1, r = 1e5;//小巧克力数量边长一定在 1 -- 100000 之间while (l < r)//二分小巧克力边长范围，找到符合要求的最大值{int mid = l + (r - l + 1 >> 1);//因为l = mid ，所以 mid 取 l + r + 1 >> 1,为了防止加和越界，改写成 l + (r - l + 1 >> 1)if (chack(mid)) l = mid;else r = mid - 1;}cout << r;
}

题目八解析

地图上有 N个目标点，用整数 X_i,Y_i表示目标在地图上的位置，每个目标都有一个价值 W_i。

注意：不同目标可能在同一位置。

现在有一种新型的激光炸弹，可以摧毁一个包含 R×R个位置的正方形内的所有目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和 x，y轴平行。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式
第一行输入正整数 N和 R，分别代表地图上的目标数目和正方形包含的横纵位置数量，数据用空格隔开。

接下来 N 行，每行输入一组数据，每组数据包括三个整数 X_i,Y_i,W_i，分别代表目标的 x 坐标，y坐标和价值，数据用空格隔开。

输出格式
输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

算法原理

代码实现

//
// Created by Genes on 2020/12/2.
//
// 激光炸弹#include <algorithm>
#include <iostream>#define ios                               \ios::sync_with_stdio(false); \cin.tie(nullptr);                     \cout.tie(nullptr)using namespace std;const int N = 5e3 + 10; //不能开 1e5+10, 内存限制比较严格int s[N][N];
int n, r;int main() {ios;cin >> n >> r;r = min(5001, r); // 因为r最大可以取 10^9for (int i = 0; i < n; i++) {int x, y, w;cin >> x >> y >> w;
//        s[++x][++y]=w;  //错误s[++x][++y] += w; //右移一位, 就不需要考虑边界了, 并且必须是+=, 不能是=, 因为1个位置可能有多个目标}for (int i = 1; i <= 5001; i++) {for (int j = 1; j <= 5001; j++) {
//            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + s[i][j];s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];}}int ans = 0;for (int i = r; i <= 5001; i++) {for (int j = r; j <= 5001; j++) {ans = max(ans, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);}}cout << ans << endl;return 0;
}

题目九解析

给定一个长度为 N 的数列，A₁,A₂,…A_N，如果其中一段连续的子序列 A_i,A_i+1,…A_j 之和是 K的倍数，我们就称这个区间 [i,j]是 K倍区间。

你能求出数列中总共有多少个 K倍区间吗？

输入格式
第一行包含两个整数 N 和 K。

以下 N
行每行包含一个整数 A_i。

输出格式
输出一个整数，代表 K倍区间的数目。

算法原理

思路:一眼看去我们就可以知道这个算法用的前缀和，
分析：
求区间[l,r]的和是k的倍数的个数。求区间和，我们可以通过前缀和来求出。我们规定sum[i]表示第1个元素到第i个元素的和。那么sum[r] - sum[l-1]就是区间[l,r]的和。区间[l,r]的和是k的倍数即(sum[r] - sum[l-1])%k == 0 即sum[r]%k == sum[l-1]%k
如果你觉得文字难以理解，那么看图：

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
typedef long long ll;
int sum[N],a[N],res[N];
int n,k;
ll ans=0;
int main()
{cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];sum[i]=(sum[i-1]+a[i])%k;//前缀和取模ans+=res[sum[i]];//更新答案  res[sum[i]]++;//两个相等的前缀和就能组成一个k倍区间}cout<<ans+res[0]<<endl;return 0;
}