目录
题目
思路
普通思路
动态规划思路
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
代码
空间优化
题目
题目链接
面试题 08.01. 三步问题![]() https://leetcode.cn/problems/three-steps-problem-lcci/
https://leetcode.cn/problems/three-steps-problem-lcci/
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3 输出:4 说明: 有四种走法
示例2:
输入:n = 5 输出:13
提示:
- n范围在[1, 1000000]之间
思路
普通思路
小孩每次可以走1步,2步,3步,我们可以将地面看成第0级台阶
当n=1时,也就是只有一级台阶,很明显可以看出,只有一种方式就是从0->1
当n=2时,也就是有两个台阶,
因为小孩可以一次性走两步,所以可以直接从0->2这是一种,
还有一种就是先上道前面的台阶,然后在到2,有1,而上到1有一种方式(0->1)。所以也是只有一种情况(0->1->2)。
根据以上分析,当n=2时,有2(1+1)种方式上台阶.

当n=3时,也就是有三个台阶
小孩可以一次性走三步,所以第一种方法,0->3
其他方法,小孩可以先上到前面台阶上,在上到3,
当小孩先上到2,再走一步就到三,上到二有两种方法(0->2,0->1->2))所以在这个情况下有两种方式(0->2->3,0->1->2->3)
当小孩先上到1,在走两步就到3,而上到1只有一种方式,所以这种方式就是0->1->3
根据以上分析,当n=3时,有4(1+2+1)种方式上台阶
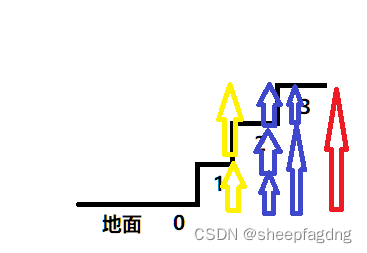
当n=4时,也就是有4个台阶
因为小孩不可以一次走四步,所以就是先上到前面台阶,然后到第四台阶.
1)先到第三台阶再走一步到第四台阶,到第三台阶根据前面分析有四种方法(这里就不列举了)
2)先到第二台阶再走两步到第四台阶,到第二台阶有两种方法
3)先到第一台阶再走三步到第四台阶,到第一台阶有一种方法
所以当n等于4时,有7种(4+2+1)方法
当n=5时,也就是有五个台阶
因为小孩不可以一次走五步,所以就是先上到前面台阶,然后到第五台阶.
1)先到第四台阶再走一步到第五台阶,到第四台阶根据前面分析有七种方法(这里就不列举了)
2)先到第三台阶再走两步到第五台阶,到第三台阶有四种方法
3)先到第二台阶再走三步到第五台阶,到第二台阶有二种方法
4)先到第一台阶,小孩也不能一次走四步 ,所以这种情况不存在
所以当n等于5时,有13种(7+4+2)方法
根据以上分析,发现此问题,跟泰波那锲数列问题没有太大差别,都是当前项的值,等于前三项之和。
动态规划思路
1.状态表示
dp表里面的值表示的含义就是一个状态表示。
本题就是,dp[i]表示,到达第i个台阶的方法有几种,根据上面普通思路的分析,创建一个名为dp的一维数组,可以把台阶数看成一维数组的下标

2.状态转移方程
状态转移方程就是:dp[i]等于什么?
当i>3时 ,dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
3.初始化
初始化就是:保证填表的时候不越界,对该初始化的值要进行初始化
本题的初始化就是,前三级台阶;
4.填表顺序
确定填表顺序是为了填写当前状态时,所需要的状态已经计算过了
因为当前项等于前三相加,所以只能先算前面的,填表顺序就是从左往右
5.返回值
根据题目要求和状态表示返回我们要的答案
本题就是dp[i]
代码
代码和泰波那锲数一样,改一下初始化和范围 ,具体详情参考 ---泰波那锲数列问题
因为n值会出现非常大的情况,这个时候要注意,数值过大问题题目里面告诉我们“对结果模1000000007”,所以每次相加都要对取模
int waysToStep(int n){int dp[1000000]={0};//初始化dp[1]=1;dp[2]=2;dp[3]=4;//边界if(n==1)return 1;if(n==2)return 2;if(n==3)return 4;//填表for(int i=4;i<=n;i++){dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;}//返回值return dp[n];}
空间复杂度:O(n)
时间复杂度:O(n)
空间优化
也是利用滚动数组,具体详情参考 ---泰波那锲数列问题
int waysToStep(int n){//初始化int a=1,b=2,c=4,d=0;//边界if(n==1)return 1;if(n==2)return 2;if(n==3)return 4;while(n>3){//计算d=((a+b)%1000000007+c)%1000000007;//滚动操作a=b;b=c;c=d;n--;}return d;
}空间复杂度:O(1)
时间复杂度:O(n)