一段代码解释：

#include <iostream>
using namespace std;
void swap1(int &a,int &b){int t;t=a;a=b;b=t;
}
void swap2(int a,int b){int t;t=a;a=b;b=t;cout<<"I'm the answer of swap2 : "<<a<<" "<<b<<endl;
}
int main(){int a=5,b=3;swap2(a,b);cout<<a<<" "<<b<<endl;swap1(a,b);cout<<a<<" "<<b<<endl;return 0;
}

运行结果：

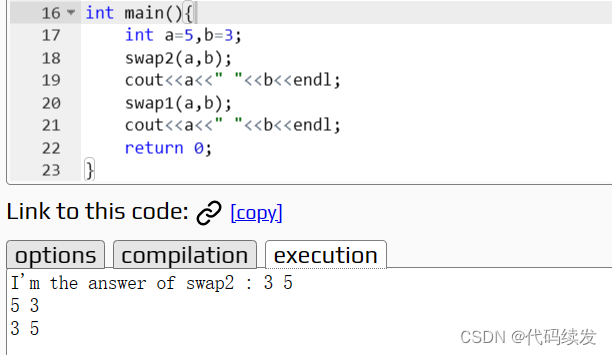
总结：

未使用取地址符时，我们只是将调用函数即swap2中的形参a,b，即副本进行了交换，实际参数存储空间中存储的值仍未改变。
而当我们使用取地址符后，我们则是对实际参数存储空间进行操作，实现将空间存储的值进行交换，即实现实参值的交换。