你好你好!
以下内容仅为当前认识,可能有不足之处,欢迎讨论!
文章目录
- torch.sum()
- torch.argmax()
- torch.nn.Parameter
- torch.unbind
- torch.optim.Adam()[^adam]
- torch.cat
- torch.unsqueeze()
- torch.normalize()[^l2]
- torch.eye
- torch.mm
- torch.view
- torch.masked_select
- torch.max
- torch.expand()[^expand]
- torch.ndimension()
- torch.range&arange
torch.sum()
torch.sum()维度0,1,2。比如现在有 3 × 2 × 3 3\times\ 2\times3 3× 2×3的张量,理解为3个 2 × 3 2\times3 2×3的矩阵。当dim=0,1,2时分别在哪个维度上相加1?下面是具体的矩阵
[ 1 , 2 , 3 ] [ 4 , 5 , 6 ] [ 1 , 2 , 3 ] [ 4 , 5 , 6 ] [ 1 , 2 , 3 ] [ 4 , 5 , 6 ] [1,2,3]\\ [4,5,6]\\\\ [1,2,3] \\ [4,5,6]\\\\ [1,2,3] \\ [4,5,6]\\\\ [1,2,3][4,5,6][1,2,3][4,5,6][1,2,3][4,5,6]
$$
\begin{bmatrix}
1&2&3
\end{bmatrix}
\begin{bmatrix}
4&5&6
\end{bmatrix}
\begin{bmatrix}
1&2&3
\end{bmatrix}
\begin{bmatrix}
4&5&6
\end{bmatrix}
$$
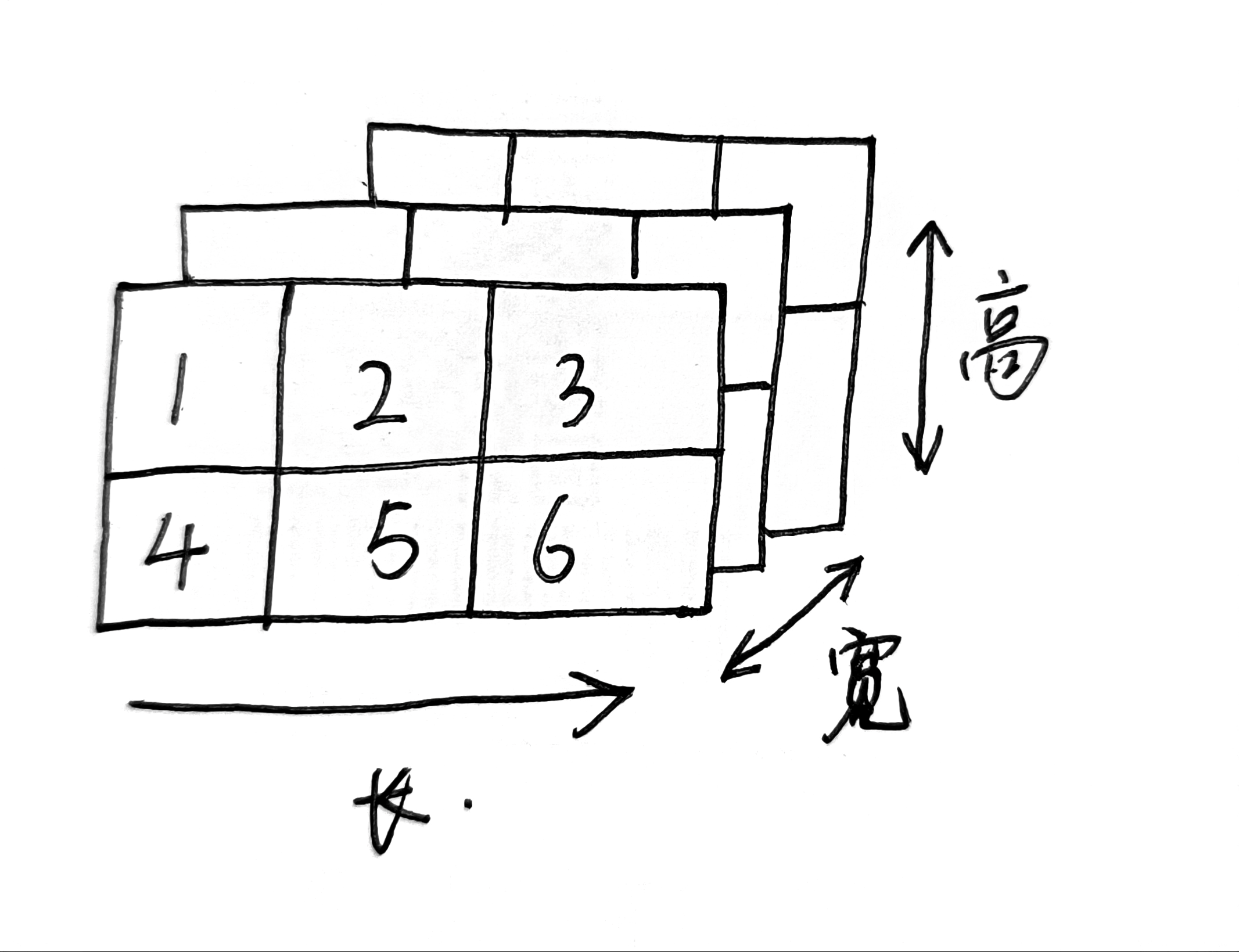
在哪个维度相加,那个维度就去掉。 3 × 2 × 3 3\times2\times3 3×2×3分别就对应0,1,2三个维度。
- dim=0,最后计算结果就是 2 × 3 2\times3 2×3。(可视化后按照宽维度相加对应元素)
- dim=1,最后计算结果就是 3 × 3 3\times3 3×3。(可视化后按照高维度相加对应元素)
- dim=2,最后计算结果就是 3 × 2 3\times2 3×2。(可视化后按照长维度相加对应元素)
宽和高维度是正面看的,所以不用动。而长维度是横着看,所以最后元素需要向左旋转。(具体计算时理解的,我这么表述可能不清楚)
示例代码
import torch
c = torch.tensor([[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]]])
print(f" c size = {c.size()}")c1=torch.sum(c , dim=0)
print(f" c1 = {c1}\n c1 size = {c1.size()}")c2=torch.sum(c , dim=1)
print(f" c2 = {c2}\n c2 size = {c2.size()}")c3=torch.sum(c , dim=2)
print(f" c3 = {c3}\n c3 size = {c3.size()}")
运行结果如下

torch.argmax()
argmax函数参数dim=0表示从列获取最大值索引,dim=1从行获取最大值索引,dim=-1从最后一个维度获取最大值索引2。
举例
import torch
d = torch.tensor([[9,7,6],[4,8,2],[5,10,0]])
print(torch.argmax(d , dim=0))#结果应为9,10,6的所在列的索引==》0,2,0
print(torch.argmax(d , dim=1))#结果应为9,8,10所在行的索引==》0,1,1
print(torch.argmax(d , dim=-1))#结果应为9,8,10所在行的索引==》0,1,1
运行结果

torch.nn.Parameter
参数是张量子类,当与模块S一块使用时,有一个非常特殊的属性——当它们被赋予为模块属性时,它们会自动添加到它的参数列表中,并且会出现在参数迭代器中。分配张量没有像这样的效果,因为可能需要在模型中缓存一些临时状态,比如RNN的上一个隐藏状态。如果没有参数这样的类,那么这些临时类也会被注册。
torch.unbind
移除一个维度,返回元组(该元组包含给定维度上已经没有的所有切片)。
import torch
a = torch.ones((2,3,1))
print(f"a-size = {a.size()}")
e = torch.unbind(a)
print(f"e type is {type(e)} , e = {e}")
print(F"e[0].size() = {e[0].size()}")
运行结果

可以看到将第一个维度移除,默认dim=0,根据张量维度,可以将dim设置为[0,(dim-1)]。
如果原先张量是 3 × 3 3\times3 3×3,移除第一个维度后,就变为3个 1 × 3 1\times3 1×3的张量。
torch.optim.Adam()[^adam]
torch.optim是一个实现了多种优化算法的包,大多数通用的方法都已支持,提供了丰富的接口调用。要使用优化算法,需先构造一个优化器对象Optimizer,用来保存当前状态,并能够根据计算得到的梯度来更新参数。
方式1:给定一个可进行迭代优化的包含所有参数的列表(所有参数必须是变量)。然后可以指定程序优化特定的选项,例如学习速率,权重衰减等。
import torchoptimizer = optim.SGD(model.parameters() , lr =0.01 , momentum = 0.9 )
#model.parameters()表示模型的所有参数,lr是学习率,momentum还不知道是啥。optimizer = optim.Adam([var1 , var2] , lr = 0.0001)
方式2:optimizer支持指定每个参数选项,只需要传递一个可以迭代的dict来替换先前可以迭代的variable。dict的每一项都可以定义为一个单独的参数组(我理解的是字典),参数组用params键来包含属于它的参数列表。其他键应该与optimizer接受的关键字参数相匹配,才能用此组的优化选项。
optim.SGD([
{'params':model.base.parameters()},
{'params':model.classifier.parameters() , 'lr':1e-3}
] , lr = 1e-2 , momentum = 0.9)
如上,model.base.parameters()将使用lr = 1e-2的学习率,model.classifier.parameters()将使用1e-3的学习率,0.9的momentum将作用于所有的parameters。
优化步骤:
优化器实现了step()方法对所有参数进行更新,有两种调用方法。
①optimizer.step()这是大多数优化器都支持的简化版本,使用backward()方法计算梯度时会调用它。
for input , target in dataset:optimizer.zero_grad()output = model(input)loss = loss_fn(output , target)loss.backward()optimizer.step()
这只是使用方法,但优化器的具体原理还没搞懂。
torch.cat
连接相同维度的张量。举例
a4=torch.tensor([[1., 1., 1.],[1., 1., 1.]])
b1=torch.tensor([[3., 3., 3.],[3., 3., 3.]])print(F"行(维度为0)连接结果{torch.cat((a4,b1) , dim=0)}")
print("="*100)
print(F"列(维度为1)连接结果{torch.cat((a4,b1),dim =1)}")

torch.unsqueeze()
在原有维度上加个维度。dim可以理解为变换后的位置为1
举例
a4=torch.tensor([[1., 1., 1.],[1., 1., 1.]])
b1=torch.tensor([[3., 3., 3.],[3., 3., 3.]])a4_new = torch.unsqueeze(a4 , dim = 0)
#在新的维度第0个位置为1,所以结果应为1×2×3
b1_new = torch.unsqueeze(b1 , dim = 1)
#在新的维度第1个位置为1,所以结果应为2×1×3
ab_new = torch.unsqueeze(a4 , dim = 2)
#在新的维度第2个位置为1,所以结果应为2×3×1
print(F"\t 0维上新加:{a4_new} \n\t a4_new形状为{a4_new.size()}")
print(F"\n")
print(F"\t 1维上新加:{b1_new} \n\t b1_new形状为{b1_new.size()}")
print(f"\n")
print(F"\t 2维上新加:{ab_new} \n\t ab_new形状为{ab_new.size()}")
结果

dataset & dataloader 详解
https://blog.csdn.net/loveliuzz/article/details/108756253
torch.normalize()[^l2]
L2范数归一化
向量 x ( x 1 , x 2 , . . . , x n ) x(x_1,x_2,...,x_n) x(x1,x2,...,xn)的L2范数定义为: n o r m ( x ) = x 1 2 + x 2 2 + . . . + x n 2 \mathrm{norm}(x)=\sqrt{x_1^2+x_2^2+...+x_n^2} norm(x)=x12+x22+...+xn2。要使得x归一化到单位L2范数,就是建立一个 x x x到 x ′ x^{'} x′的映射,使得 x ′ x^{'} x′的L2范数为1。
即 x i ′ = x i n o r m ( x ) x_i^{'}=\dfrac{x_i}{\mathrm{norm}(x)} xi′=norm(x)xi。
举例
x = torch.tensor([[1,2,4] , [3,5,6] , [9, 3, 1]] , dtyp= torch.float)
y = torch.nn.functional.normalize(x , dim = 0)
z = torch.nn.functional.normalize(x , dim = 1)
print(f"y = {y}")
print(f"z = {z}")

dim = 0 ,从列计算。
dim = 1,从行计算。
为什么要进行归一化?归一化有什么好处?
可以提高深度学习模型收敛速度,如果不进行归一化,假设模型接受的输入向量有两个维度x,y,其中x取值[0,1000],y取值[0,10]。这样数据在进行梯度下降计算时梯度对应一个很扁的椭圆形,很容易在垂直等高线的方向上走大量的之字形路线,迭代量大且迭代次数多,造成模型收敛慢[^why l2]。
损失函数是自己写的,既然是自己写的,那怎么求导呢?那怎么反向传播呢?
有训练次数,有自己的函数指导
torch.eye
生成一个二维对角矩阵,参数是 n × m n\times m n×m。
举例
mask = torch.eye((3) ,dtype = torch.bool )
print(mask)
结果👇

torch.mm
torch.mm(input , mat2 , * , out = None)-> Tensor
两个矩阵相乘
举例
a = torch.tensor([[1,2,3],[4,5,6]])
b = torch.tensor([[1,2],[3,4],[5,6]])
c = torch.mm(a , b)
print(f"\t c={c}")

torch.view
输入:形状,不知道的维度可以用-1。
返回:一个数据与自张量相同但形状不同的新张量
举例
x = torch.randn(4,4)
print(f" x = {x} \n x.size() = {x.size()}")
y = x.view(-1)
z = x.view(16)
q = x.view(2,-1)
p = x.view(-1,8)
print(f" y = {y} \n y.size() = {y.size()}")
print(f" z = {z} \n z.size() = {z.size()}")
print(f" q = {q} \n q.size() = {q.size()}")
print(f" p = {p} \n p.size() = {p.size()}")
运行结果

torch.masked_select
输入参数:输入张量,布尔值掩码
返回:一个新的1-D张量,该张量根据布尔值掩码对输入张量进行判定,为True则记录,返回之。
举例
x = torch.tensor([[-1,2,-4],[2,-5,8],[-3,6,-9]])
print(f"x = {x}")
print(f"x.size() = {x.size()}")mask = x.ge(0.5)
print(f"mask = {mask}")
print(f"mask.size() = {mask.size()}")y = torch.masked_select(x , mask)
print(f"y = {y}")
print(f"y.size() = y.size()")
运行结果

因为数据总量是不同的,所以不能总是按照自己手动算的结果作为最终的形状输入。这时就需要用到view函数。(2024年1月3日)
torch.max
返回输入张量所有元素的最大值。
举例
x = torch.randn([3,3])
print(f"\tx = {x}")
max = torch.max(x)
print(F"\tmax = {max}")
max2 = x.max(0)
print(f"\tmax2 = {max2}")
max3 = x.max(1)
print(F"\tmax3 = {max3}")维度为0返回列的最大值,及所在列元素位置的索引
维度为1返回行的最大值,及所在行元素位置的索引

torch.expand()[^expand]
返回新的视图,其中单维尺寸扩展到更大的尺寸。如果参数是-1意味着不更改该维度。
举例,现在有 2 × 3 2\times3 2×3的张量矩阵,现在想将它扩展为 4 × 4 4\times4 4×4的矩阵。显示不可行,需要倍数关系。
a = torch.tensor([[1,3,5],[2,4,5]])
b = a.expand(4,4)
c = a.expand(-1,4)
print(f"\t a = {a}")
print(f"\t b = {b}")
print(f"\t c = {c}")

那现在 2 × 3 → 4 × 6 2\times3\rightarrow4\times6 2×3→4×6。
a = torch.tensor([[1,3,5],[2,4,5]])
b = a.expand(4,6)
c = a.expand(-1,6)
print(f"\t a = {a}")
print(f"\t b = {b}")
print(f"\t c = {c}")
也不行,只能由原先维度为1所在维度进行扩张。其他维度不知道的话可以写成-1。
a = torch.tensor([[1,3,4]])
print(f"\t size of a = {a.size()}\n")
b = a.expand(6,-1)
print(f"\t size of b = {b.size()}\n\t b = {b}")

torch.ndimension()
得到这个矩阵的维度是什么
a = torch.ones((1,2,3))
b = torch.tensor([1,3,3,5])
c = torch.tensor([[1,2,3,4],[5,7,5,3]])
a_dim = a.ndimension()
b_dim = b.ndimension()
c_dim = c.ndimension()
print(f"\t a的形状是{a.size()},a的维度是{a_dim}")
print(F"\t b的形状是{b.size()},b的维度是{b_dim}")
print(F"\t c的形状是{c.size()},c的维度是{c_dim}")
torch.tensor.index_add_()[^index_add]
作用
参数
返回值
torch.to_dense()&sparse_coo_tensor()
作用
参数
返回值
torch.range&arange
以上是我的学习笔记,希望对你有所帮助!
如有不当之处欢迎指出!谢谢!

https://mathpretty.com/12065.html#%E5%AF%B9%E4%BA%8E%E4%B8%89%E7%BB%B4%E5%90%91%E9%87%8F ↩︎
https://blog.csdn.net/weixin_42494287/article/details/92797061 ↩︎