思路：本题一开始想到的肯定是用多层for循环嵌套，但是需要k层，而k是变量，故使用这种暴力方法写不出来，必须使用递归。我一开始还是想根据k来递归，但是无法写出来。看了解析需要使用树形结构来理解回溯过程。

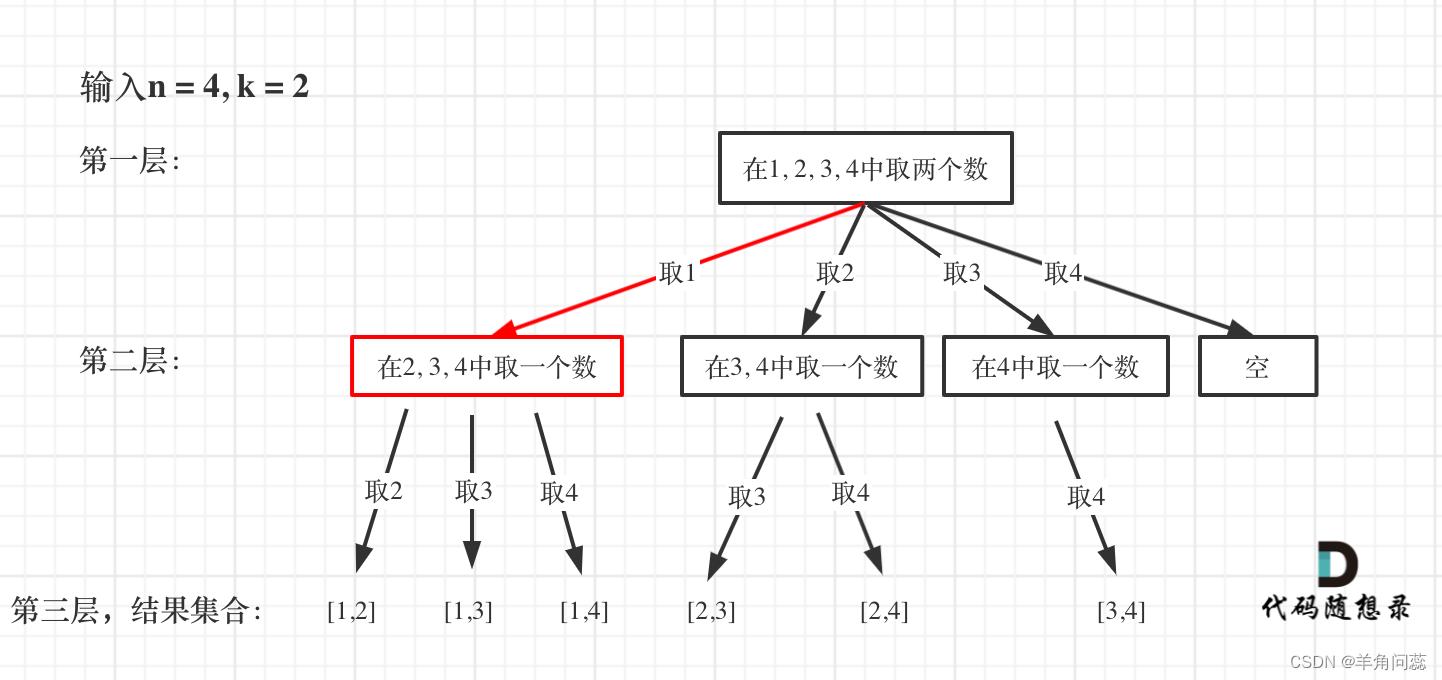
取数的过程可以首先取第一个数，然后在剩下三个数里取出第二个数，得到结果；然后回溯，取第二个数，然后继续类推。故递归参数还需要一个取的第一个数的下标，递归在取的数的数量为k的时候终止。其中for循环用于横向遍历，递归用于纵向深度遍历。时间复杂度O(n*2^n)，指数级别，可以看到是暴力搜索。

class Solution {
public:vector<vector<int>> ans;vector<int> path;void backtracking(int n,int k,int start){if(path.size()==k){ans.push_back(path);return;}for(int i=start;i<=n;i++){path.push_back(i);backtracking(n,k,i+1);//由于第一个数已经取了i，剩下就从i+1开始取path.pop_back();//回溯，撤销已经加入路径的节点}}vector<vector<int>> combine(int n, int k) {backtracking(n,k,1);return ans;}
};

一开始很容易犯的一个错误是将回溯过程中的递归第二个参数写成k-1，因为看上去是第二次只取k-1个数，实际上此时的k的作用主要是用于判断递归是否终止，是否终止是根据已经求出的深度决定的，故k需要保持不变。
可以进行适当剪枝，比如start的结尾值不需要为n，可以为 n-(k-path.size())+1 ，因为后续都不满 k-path.size() 个数了，自然不可能取到。 k-path.size() 为一条路径还需要取的数的个数。

class Solution {
public:vector<vector<int>> ans;vector<int> path;void backtracking(int n,int k,int start){if(path.size()==k){ans.push_back(path);return;}for(int i=start;i<=n-(k-path.size())+1;i++){path.push_back(i);backtracking(n,k,i+1);//由于第一个数已经取了i，剩下就从i+1开始取path.pop_back();//回溯，撤销已经加入路径的节点}}vector<vector<int>> combine(int n, int k) {backtracking(n,k,1);return ans;}
};

思路如下图所示：

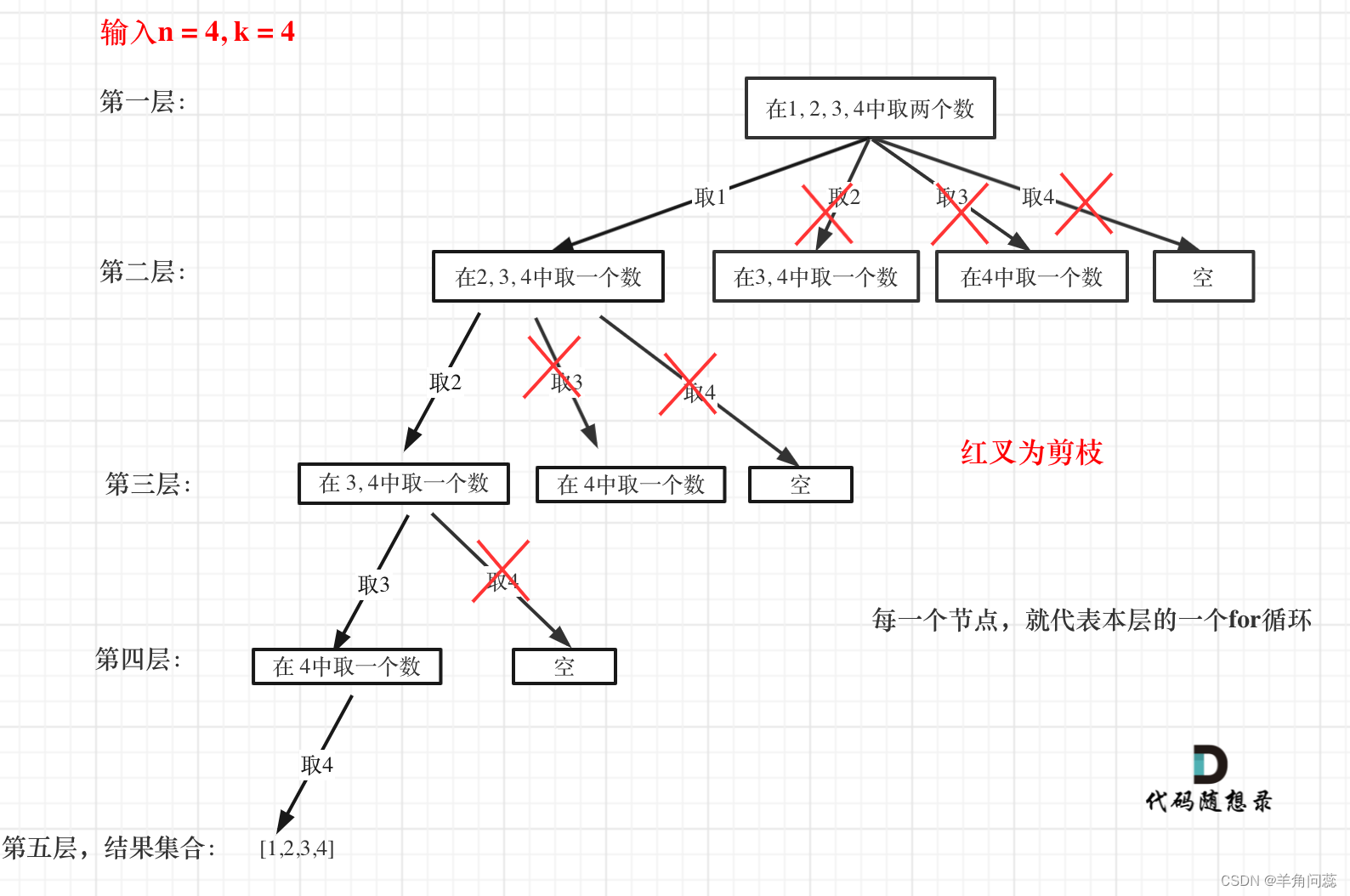
回溯法刚开始学多借助图来理解。