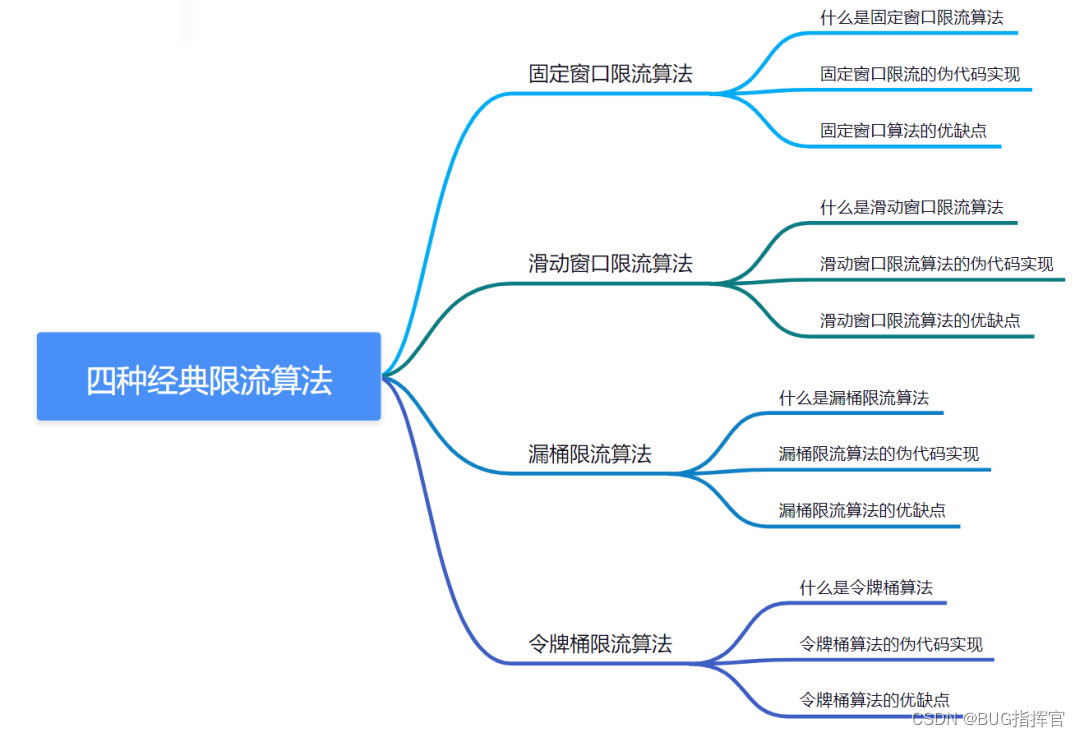
1. 固定窗口限流算法

1.1 什么是固定窗口限流算法

固定窗口限流算法（Fixed Window Rate Limiting Algorithm）是一种最简单的限流算法，其原理是在固定时间窗口(单位时间)内限制请求的数量。该算法将时间分成固定的窗口，并在每个窗口内限制请求的数量。具体来说，算法将请求按照时间顺序放入时间窗口中，并计算该时间窗口内的请求数量，如果请求数量超出了限制，则拒绝该请求。

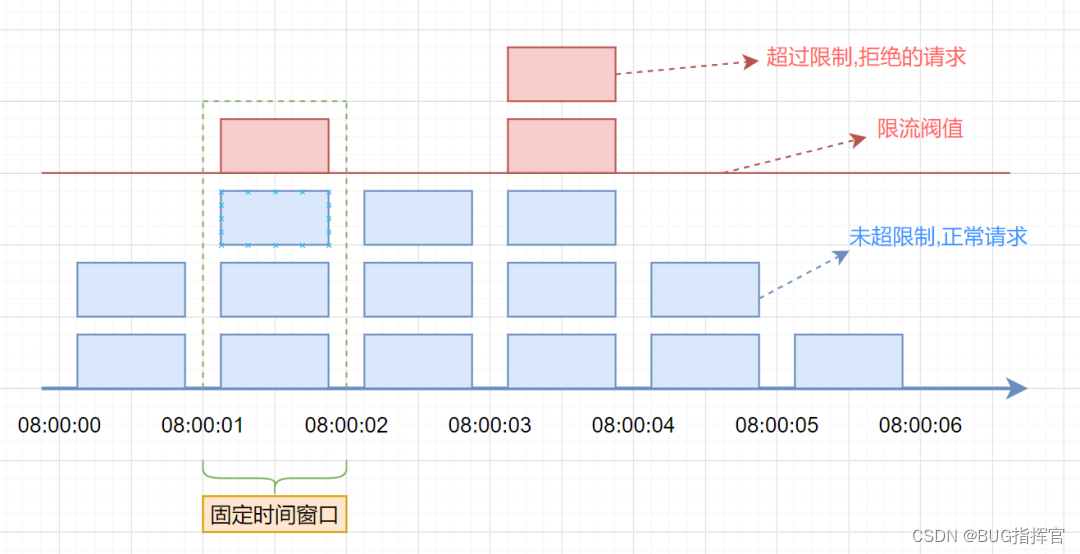
假设单位时间(固定时间窗口)是1秒，限流阀值为3。在单位时间1秒内，每来一个请求,计数器就加1，如果计数器累加的次数超过限流阀值3，后续的请求全部拒绝。等到1s结束后，计数器清0，重新开始计数。如下图：

1.2 固定窗口限流的伪代码

   public static Integer counter = 0;  //统计请求数public static long lastAcquireTime =  0L;public static final Long windowUnit = 1000L ; //假设固定时间窗口是1000mspublic static final Integer threshold = 10; // 窗口阀值是10/*** 固定窗口时间算法* @return*/public synchronized boolean fixedWindowsTryAcquire() {long currentTime = System.currentTimeMillis();  //获取系统当前时间if (currentTime - lastAcquireTime > windowUnit) {  //检查是否在时间窗口内counter = 0;  // 计数器清0lastAcquireTime = currentTime;  //开启新的时间窗口}if (counter < threshold) {  // 小于阀值counter++;  //计数统计器加1return true;}return false;}

1.2 固定窗口算法的优缺点

• 优点：固定窗口算法非常简单，易于实现和理解。

• 缺点：存在明显的临界问题，比如: 假设限流阀值为5个请求，单位时间窗口是1s,如果我们在单位时间内的前0.8-1s和1-1.2s，分别并发5个请求。虽然都没有超过阀值，但是如果算0.8-1.2s,则并发数高达10，已经超过单位时间1s不超过5阀值的定义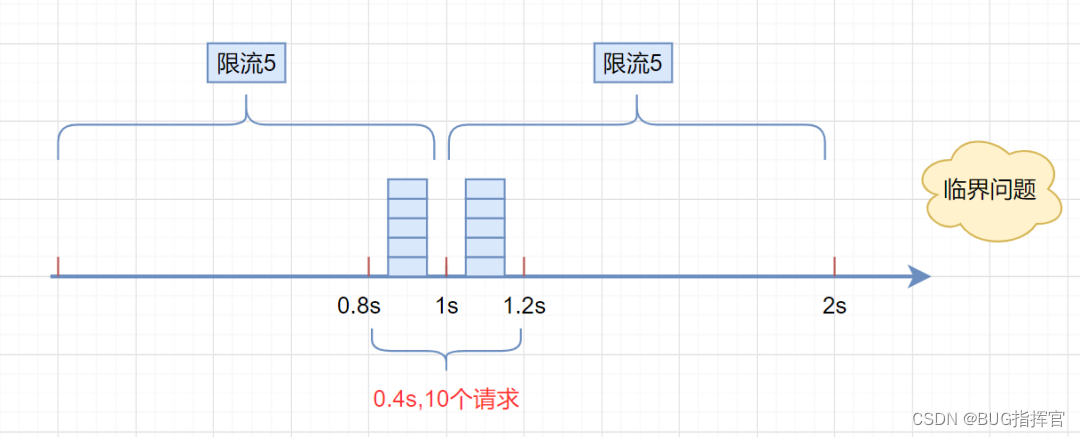

2. 滑动窗口限流算法

2.1 什么是滑动窗口限流算法

滑动窗口限流算法是一种常用的限流算法，用于控制系统对外提供服务的速率，防止系统被过多的请求压垮。它将单位时间周期分为n个小周期，分别记录每个小周期内接口的访问次数，并且根据时间滑动删除过期的小周期。它可以解决固定窗口临界值的问题。

用一张图解释滑动窗口算法，如下：

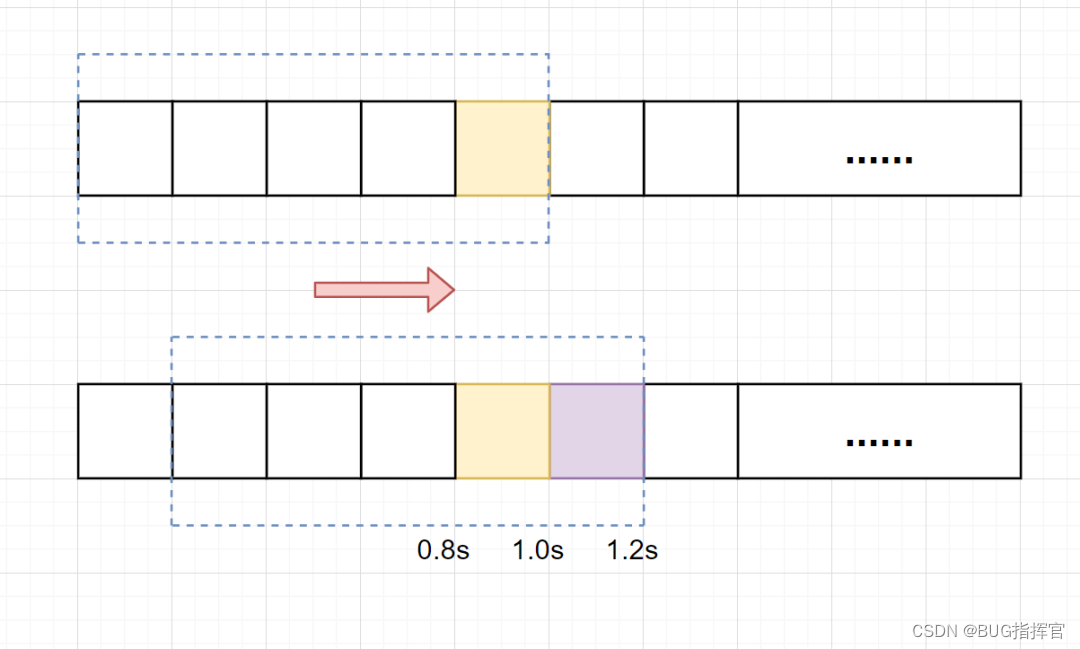
假设单位时间还是1s，滑动窗口算法把它划分为5个小周期，也就是滑动窗口（单位时间）被划分为5个小格子。每格表示0.2s。每过0.2s，时间窗口就会往右滑动一格。然后呢，每个小周期，都有自己独立的计数器，如果请求是0.83s到达的，0.8~1.0s对应的计数器就会加1。

我们来看下，滑动窗口,去解决固定窗口限流算法的临界问题，思想是怎样

假设我们1s内的限流阀值还是5个请求，0.8~1.0s内（比如0.9s的时候）来了5个请求，落在黄色格子里。时间过了1.0s这个点之后，又来5个请求，落在紫色格子里。如果是固定窗口算法，是不会被限流的，但是滑动窗口的话，每过一个小周期，它会右移一个小格。过了1.0s这个点后，会右移一小格，当前的单位时间段是0.2~1.2s，这个区域的请求已经超过限定的5了，已触发限流啦，实际上，紫色格子的请求都被拒绝啦。

当滑动窗口的格子周期划分的越多，那么滑动窗口的滚动就越平滑，限流的统计就会越精确。

2.2 滑动窗口限流算法的伪代码实现

 /*** 单位时间划分的小周期（单位时间是1分钟，10s一个小格子窗口，一共6个格子）*/private int SUB_CYCLE = 10;/*** 每分钟限流请求数*/private int thresholdPerMin = 100;/*** 计数器, k-为当前窗口的开始时间值秒，value为当前窗口的计数*/private final TreeMap<Long, Integer> counters = new TreeMap<>();/*** 滑动窗口时间算法实现*/public synchronized boolean slidingWindowsTryAcquire() {long currentWindowTime = LocalDateTime.now().toEpochSecond(ZoneOffset.UTC) / SUB_CYCLE * SUB_CYCLE; //获取当前时间在哪个小周期窗口int currentWindowNum = countCurrentWindow(currentWindowTime); //当前窗口总请求数//超过阀值限流if (currentWindowNum >= thresholdPerMin) {return false;}//计数器+1counters.get(currentWindowTime)++;return true;}/*** 统计当前窗口的请求数*/private int countCurrentWindow(long currentWindowTime) {//计算窗口开始位置long startTime = currentWindowTime - SUB_CYCLE* (60s/SUB_CYCLE-1);int count = 0;//遍历存储的计数器Iterator<Map.Entry<Long, Integer>> iterator = counters.entrySet().iterator();while (iterator.hasNext()) {Map.Entry<Long, Integer> entry = iterator.next();// 删除无效过期的子窗口计数器if (entry.getKey() < startTime) {iterator.remove();} else {//累加当前窗口的所有计数器之和count =count + entry.getValue();}}return count;}

2.3 滑动窗口限流算法的优缺点

优点：

• 简单易懂

• 精度高（通过调整时间窗口的大小来实现不同的限流效果）

• 可扩展性强（可以非常容易地与其他限流算法结合使用）

缺点：

• 突发流量无法处理（无法应对短时间内的大量请求，但是一旦到达限流后，请求都会直接暴力被拒绝。酱紫我们会损失一部分请求，这其实对于产品来说，并不太友好），需要合理调整时间窗口大小。

3. 漏桶限流算法

3.1 什么是漏桶限流算法

漏桶限流算法（Leaky Bucket Algorithm）是一种流量控制算法，用于控制流入网络的数据速率，以防止网络拥塞。它的思想是将数据包看作是水滴，漏桶看作是一个固定容量的水桶，数据包像水滴一样从桶的顶部流入桶中，并通过桶底的一个小孔以一定的速度流出，从而限制了数据包的流量。

漏桶限流算法的基本工作原理是：对于每个到来的数据包，都将其加入到漏桶中，并检查漏桶中当前的水量是否超过了漏桶的容量。如果超过了容量，就将多余的数据包丢弃。如果漏桶中还有水，就以一定的速率从桶底输出数据包，保证输出的速率不超过预设的速率，从而达到限流的目的。

• 流入的水滴，可以看作是访问系统的请求，这个流入速率是不确定的。

• 桶的容量一般表示系统所能处理的请求数。

• 如果桶的容量满了，就达到限流的阀值，就会丢弃水滴（拒绝请求）

• 流出的水滴，是恒定过滤的，对应服务按照固定的速率处理请求。

3.2 漏桶限流算法的伪代码实现

 /*** LeakyBucket 类表示一个漏桶,* 包含了桶的容量和漏桶出水速率等参数，* 以及当前桶中的水量和上次漏水时间戳等状态。*/
public class LeakyBucket {private final long capacity;    // 桶的容量private final long rate;        // 漏桶出水速率private long water;             // 当前桶中的水量private long lastLeakTimestamp; // 上次漏水时间戳public LeakyBucket(long capacity, long rate) {this.capacity = capacity;this.rate = rate;this.water = 0;this.lastLeakTimestamp = System.currentTimeMillis();}/*** tryConsume() 方法用于尝试向桶中放入一定量的水，如果桶中还有足够的空间，则返回 true，否则返回 false。* @param waterRequested* @return*/public synchronized boolean tryConsume(long waterRequested) {leak();if (water + waterRequested <= capacity) {water += waterRequested;return true;} else {return false;}}/*** 。leak() 方法用于漏水，根据当前时间和上次漏水时间戳计算出应该漏出的水量，然后更新桶中的水量和漏水时间戳等状态。*/private void leak() {long now = System.currentTimeMillis();long elapsedTime = now - lastLeakTimestamp;long leakedWater = elapsedTime * rate / 1000;if (leakedWater > 0) {water = Math.max(0, water - leakedWater);lastLeakTimestamp = now;}}
}

• 注意:   tryConsume() 和 leak() 方法中，都需要对桶的状态进行同步，以保证线程安全性。

3.3 漏桶限流算法的优缺点

优点

• 可以平滑限制请求的处理速度，避免瞬间请求过多导致系统崩溃或者雪崩。

• 可以控制请求的处理速度，使得系统可以适应不同的流量需求，避免过载或者过度闲置。

• 可以通过调整桶的大小和漏出速率来满足不同的限流需求，可以灵活地适应不同的场景。

缺点

• 需要对请求进行缓存，会增加服务器的内存消耗。

• 对于流量波动比较大的场景，需要较为灵活的参数配置才能达到较好的效果。

• 但是面对突发流量的时候，漏桶算法还是循规蹈矩地处理请求，这不是我们想看到的啦。流量变突发时，我们肯定希望系统尽量快点处理请求，提升用户体验嘛。

4. 令牌桶算法

4.1 什么是令牌桶算法

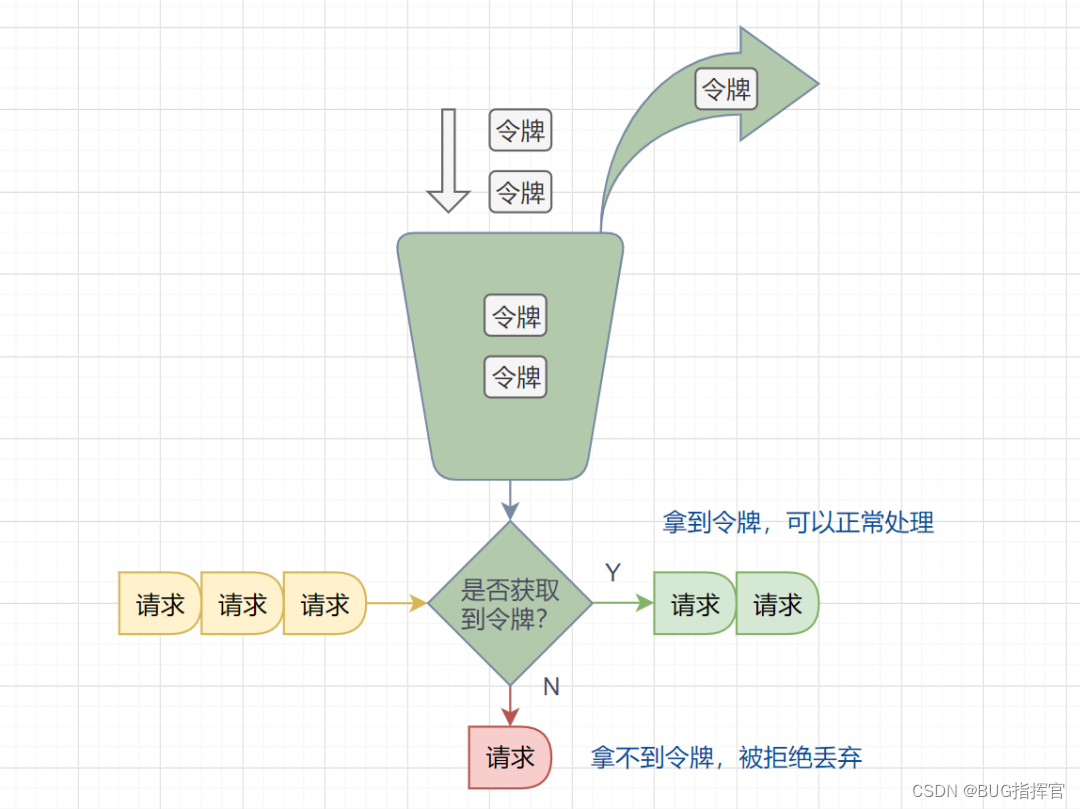
令牌桶算法是一种常用的限流算法，可以用于限制单位时间内请求的数量。该算法维护一个固定容量的令牌桶，每秒钟会向令牌桶中放入一定数量的令牌。当有请求到来时，如果令牌桶中有足够的令牌，则请求被允许通过并从令牌桶中消耗一个令牌，否则请求被拒绝。

4.2 令牌桶算法的伪代码实现

/*** TokenBucket 类表示一个令牌桶*/
public class TokenBucket {private final int capacity;     // 令牌桶容量private final int rate;         // 令牌生成速率，单位：令牌/秒private int tokens;             // 当前令牌数量private long lastRefillTimestamp;  // 上次令牌生成时间戳/*** 构造函数中传入令牌桶的容量和令牌生成速率。* @param capacity* @param rate*/public TokenBucket(int capacity, int rate) {this.capacity = capacity;this.rate = rate;this.tokens = capacity;this.lastRefillTimestamp = System.currentTimeMillis();}/*** allowRequest() 方法表示一个请求是否允许通过，该方法使用 synchronized 关键字进行同步，以保证线程安全。* @return*/public synchronized boolean allowRequest() {refill();if (tokens > 0) {tokens--;return true;} else {return false;}}/*** refill() 方法用于生成令牌，其中计算令牌数量的逻辑是按照令牌生成速率每秒钟生成一定数量的令牌，* tokens 变量表示当前令牌数量，* lastRefillTimestamp 变量表示上次令牌生成的时间戳。*/private void refill() {long now = System.currentTimeMillis();if (now > lastRefillTimestamp) {int generatedTokens = (int) ((now - lastRefillTimestamp) / 1000 * rate);tokens = Math.min(tokens + generatedTokens, capacity);lastRefillTimestamp = now;}}
}

4.3 令牌桶算法的优缺点

优点：

• 稳定性高：令牌桶算法可以控制请求的处理速度，可以使系统的负载变得稳定。

• 精度高：令牌桶算法可以根据实际情况动态调整生成令牌的速率，可以实现较高精度的限流。

• 弹性好：令牌桶算法可以处理突发流量，可以在短时间内提供更多的处理能力，以处理突发流量。

Guava的RateLimiter限流组件，就是基于令牌桶算法实现的。

缺点：

• 实现复杂：相对于固定窗口算法等其他限流算法，令牌桶算法的实现较为复杂。对短时请求难以处理：在短时间内有大量请求到来时，可能会导致令牌桶中的令牌被快速消耗完，从而限流。这种情况下，可以考虑使用漏桶算法。

• 时间精度要求高：令牌桶算法需要在固定的时间间隔内生成令牌，因此要求时间精度较高，如果系统时间不准确，可能会导致限流效果不理想。

总体来说，令牌桶算法具有较高的稳定性和精度，但实现相对复杂，适用于对稳定性和精度要求较高的场景。