一、一阶低通数字滤波器原理

一阶滤波，亦称一阶惯性滤波或一阶低通滤波。其数学表达式如下：

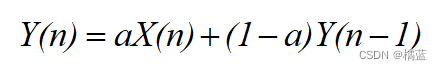
其中：α代表滤波系数；X(n)表示本次采样值；Y(n-1) 为上次滤波输出值；Y(n) 为本次滤波输出值。一阶低通滤波方法通过对本次采样值与上次滤波输出值进行加权，得出有效滤波值，从而使输出对输入产生反馈作用。
由公式可知，参数α决定了输出Y(n)中所含有的采样值X(n)的有效分量大小，α越大，X(n)的有效部分越多，原信号中的高频分量有效部分也相应增多，曲线波动性更大。α越小，X(n)的有效部分越小，上一时间Y(n-1) 的信号有效部分越多，曲线越平滑。

二、Simulink仿真实现

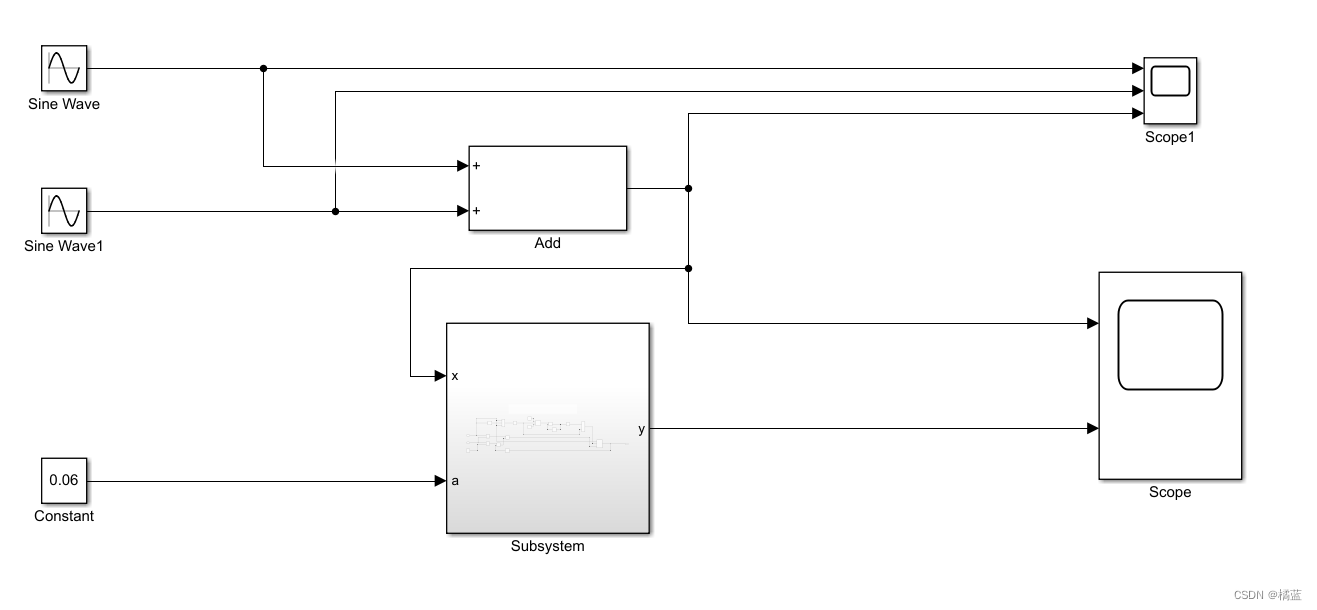
子系统模型搭建（算法实现部分）如下：

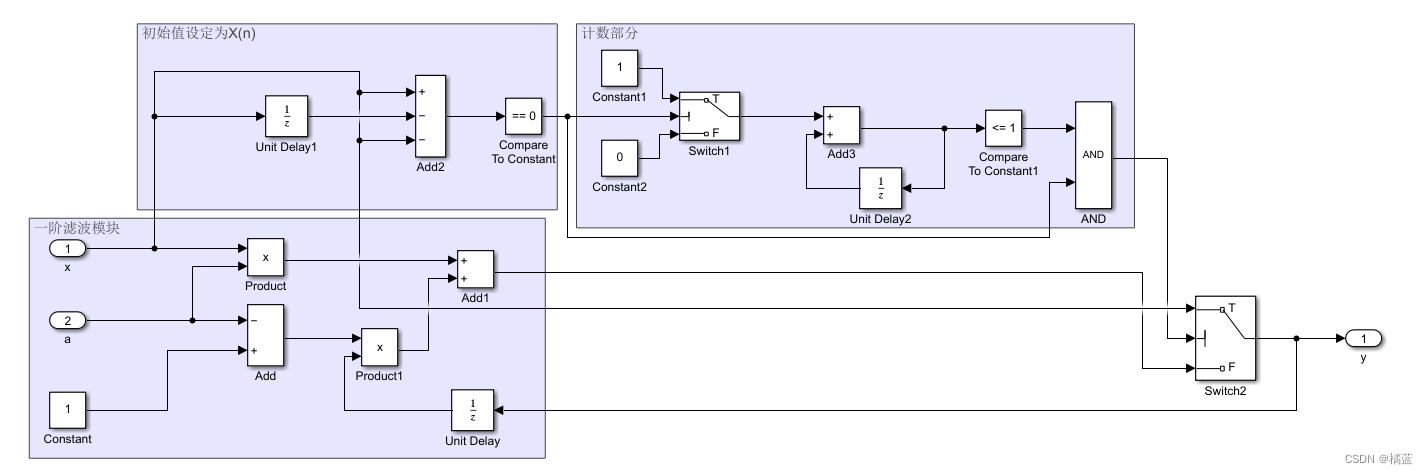
仅通过公式搭建的滤波模块存在一个问题：
当x(n)初始不从零开始时，由于0时刻X（n-1）为0，输出y(n)将从零附近开始跳变。
输入x(n)由两个正弦波叠加，参数设置为：

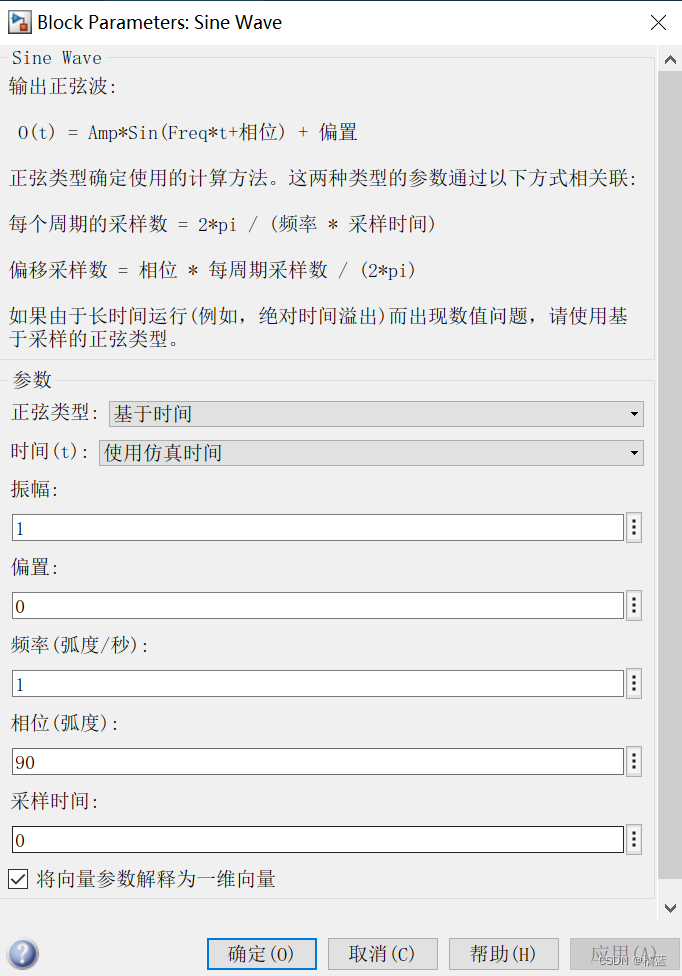
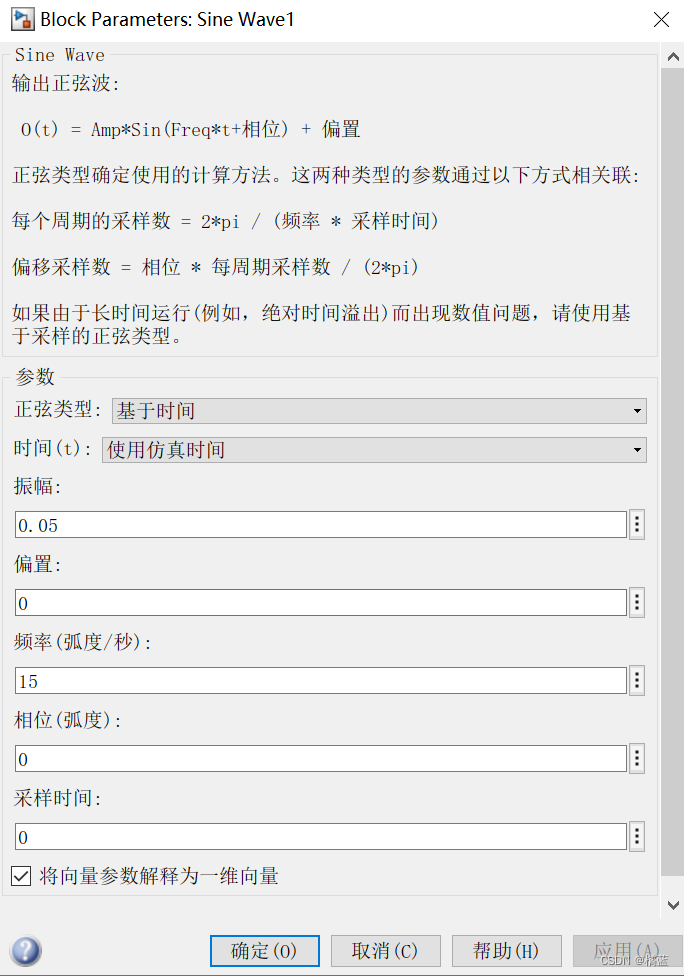
波形如图所示：

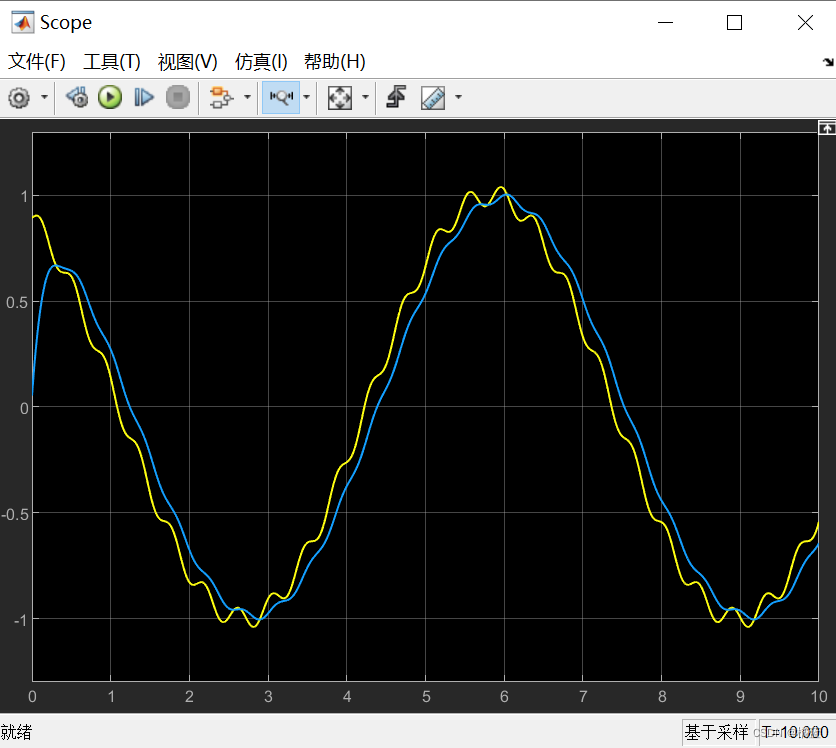
初始值x(n)不为0时，初始x(n-1)为0，y(n-1)=x(n)*a+(1-a)*0=x(n)*a极小，低频分量被滤除，导致y(n)=x(n)*a极小(约从0开始)。

解决办法：添加判断 当第一次出现x(n)-x(n-1)=x(n)时,令y(n)=x(n). 使初始从x(n)开始。

每当x(n-1)为0的时候，y(n)=x(n)，后续依然可能出现x(n)-x(n-1)=x(n)的情况，可考虑加一个计数器设置仅第一次X(n-1)时有效。
注：离散采样时不一定会采样到x(n-1)=0. 后续的累加不一定起作用，但是第一次一定能采样到，所以计数模块是有效的。
添加模块后波形如下：

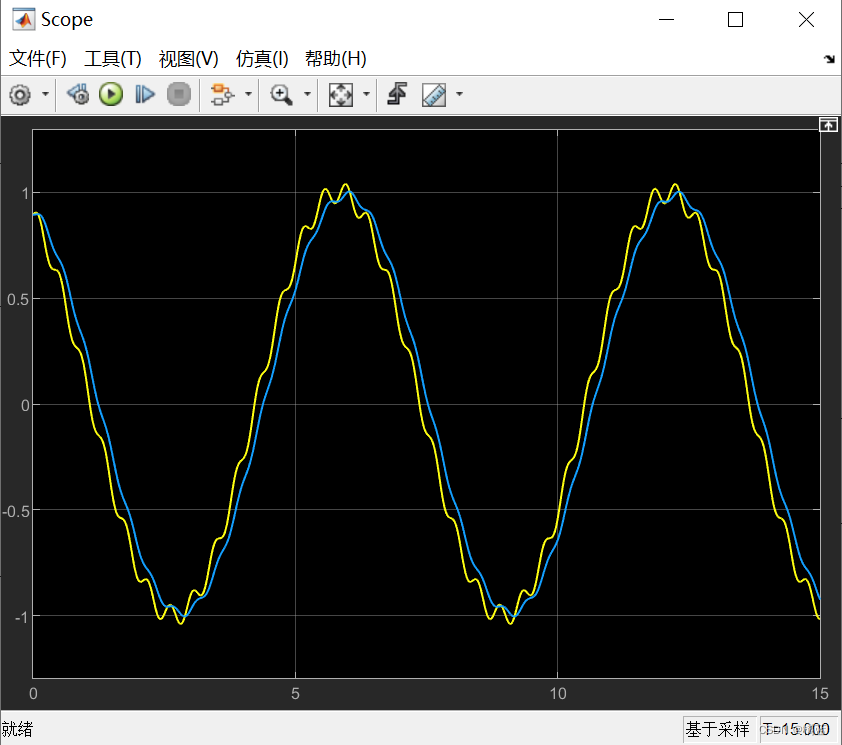
参考：

https://blog.csdn.net/m0_73931287/article/details/134040983