二叉树顺序结构——堆的实现
- 结构体的创建以及接口函数
- 结构体的创建
- 堆的初始化
- 交换函数
- 堆的插入
- 向上调整
- 删除
- 向下调整
- 返回堆的个数
- 返回堆顶数据
- 判断堆是否为空
该文章以大堆作为研究对象
结构体的创建以及接口函数
typedef int HPDateType;//定义动态数组的数据类型
typedef struct HeaP
{HPDateType* a;//指针int size;//有效数据个数,也是即将插入的下一个有效数据的下标int capacity;//容量
}HP;void HeapInit(HP* php);//堆的初始化Swap(HPDateType* a, HPDateType* b);//交换函数void AdjustUp(HPDateType* a, int child);//向上调整void HeapPush(HP* php,int x);//堆的插入void AdjustDown(HPDateType* a, int n, int parent);//向下调整void AdjustDownSmall(HPDateType* a, int n, int parent);//向下调整(小堆) void HeapPop(HP* php);//删除int HeapSize(HP* php);//返回堆的个数HPDateType HeapTop(HP* php);//返回堆顶数据bool HeapEmpty(HP* php);//判断是否为空 空返回ture 非空返回false
结构体的创建
- 宏定义一个堆的数据类型,方便堆数据类型的控制
- 堆用顺序结构来存储,由于将来会有多种接口函数对堆进行操作,所以将堆放在动态存储空间中
typedef int HPDateType;//定义动态数组的数据类型
typedef struct HeaP
{HPDateType* a;//指针int size;//有效数据个数,也是即将插入的下一个有效数据的下标int capacity;//容量
}HP;
堆的初始化
初始为堆开辟4个堆数据类型的空间,这里堆的数据类型为int ,也就初始开辟4个int的空间,16个字节的空间。
void HeapInit(HP* php)//堆的初始化
{assert(php);//断言防止空指针的引用php->a = (HPDateType*)malloc(sizeof(HPDateType) * 4);//初始容量为4if (php->a == NULL){perror("HeapInit failed");return;}php->size = 0;//初始数据为0php->capacity = 4;//初始容量为4
}
交换函数
因为交换函数在各种函数中多次运用,这里专门写一个函数来用
Swap(HPDateType* a, HPDateType* b)//交换函数
{HPDateType temp = *a;*a = *b;*b = temp;
}
堆的插入
插入函数要的任务是,新数据的插入原来堆的性质。比如下面这个大堆,100作为新数据的插入(左图),他现在的结点位置破坏了堆的性质。所有需要将新插入的数据进行调整,后面会讲到两种调整方法,这里用到的是向上调整法(原理在下面,这里建议先去下面看向上调整),向上调整后100就会到适配于这个堆的位置(右图)。
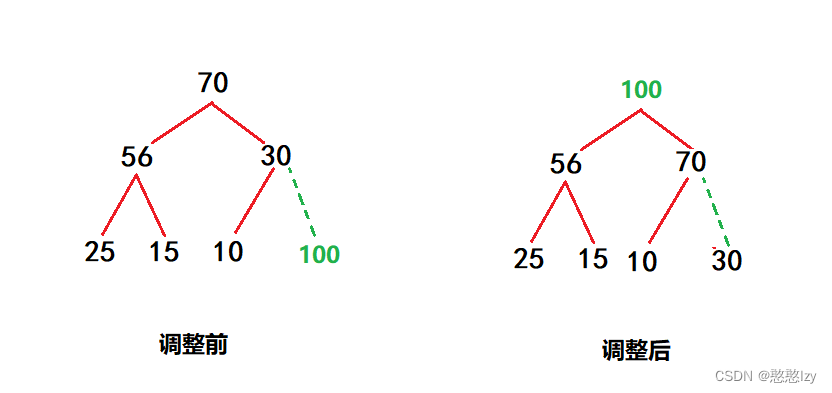
利用这个原理,若我们可以将一个数组的数据一个一个的插入到堆当中去。
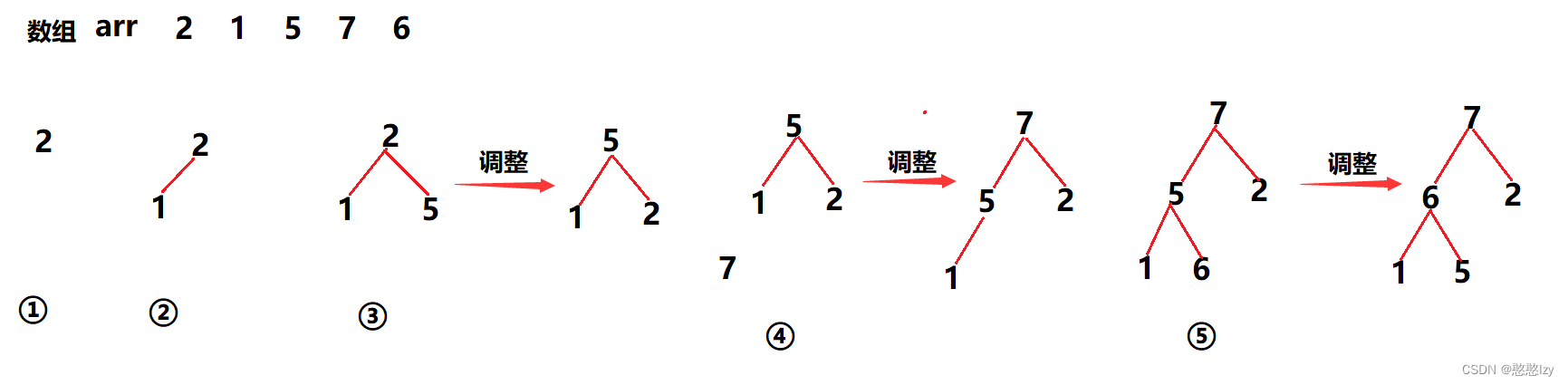
所以插入一个数据只需要赋值进来后进行向上调整
void HeapPush(HP* php, int x)//堆数据的插入
{assert(php);//防止空指针的引用php->a[php->size] = x;//插入数据AdjustUp(php->a, php->size);//新数据的插入检查是否符合堆的结构,所以直接向上调整php->size++;//堆结构体的有效数据变量自增
}
向上调整
前文说道该函数功能就是将新插入的数据调整到适配于这个堆的位置。那么怎么实现呢?
显然向上调整的条件就是首先原来的数据的结构符合一个堆。
思路就是新插入的数据和他的父亲结点比较,若孩子比父亲大则交换,反复循环;若孩子比父亲小的话符合大堆,则说明新插入的数据符合大堆,所以不需要调整;
这里向上调整函数的形参传入的是数组,因为后面还可能用到他,所以形参没有传堆结构体指针。
孩子的父亲节点parent = (child-1)/2 这个知识点也是一个要点
void AdjustUp(HPDateType* a,int child)//向上调整(大堆) 时间复杂度O(logN)
{int parent = (child - 1) / 2;//锁定要调整孩子的父亲结点while (child > 0)//最坏的情况是孩子的下标为1,父亲的下标为0,所以限制条件就是child>0{if (a[child] > a[parent]){Swap(&a[child], &a[parent]);//数据交换,也就是向上调整child = parent;//这时候原数据对应的下标也应该向上调整parent = (child - 1) / 2;//调整后的父亲节点的下标}else//孩子小于父亲节点符合大堆不需要交换{break;}}
}
删除
删除函数如果说只删除堆尾的话,虽然简单但没有意义,因为堆尾并不是一个特殊的位置,反而堆顶是一个能体现出来堆性质的一个结点,所以堆的删除一般都是删除堆顶。
那么这时候就要考虑怎么删除堆顶,然后不能将其原来的数据结构打乱。如果是平移删除的话只会将原来堆的结构打乱,大费周章。这时候会用到向下调整(建议先去下面看向下调整原理)。所以这时候删除就很简单了,首先将堆顶和堆尾交换数据,然后再size–,从堆顶的位置进行向下调整即可。
void HeapPop(HP* php)//删除
{//思路:交换堆顶和堆尾的数据,然后删除最后一个数据,然后将新的堆进行向下调整Swap(&php->a[0], &php->a[php->size - 1]);//交换第一个数据和最后一个数据php->size--;//删除数组最后一个数据AdjustDown(php->a,php->size,0);//这里size已经自减过一次了,所以传参直接传size刚好
}
向下调整
向下调整适用的条件是:调整位置的左右子树都符合堆的结构。
思路:将调整位置与其孩子结点作比较,若父亲结点小于较大的孩子结点则交换数据;若大于较大的孩子结点则不需要进行调整。
孩子结点与父亲结点的关系:
leftchild=parent * 2+1;
rightchild=parent * 2+2;
该函数的传参问题:因为方便后续的使用,形参传参一个数组和数组的大小和调整结点下标;因为要进行父亲结点和孩子结点的不断比较,需要存储堆数据的数组的元素个数作为循环的限制条件,所以要传参一个n,例如

void AdjustDown(HPDateType* a, int n, int parent)//向下调整 时间复杂度O(logN)
//向下调整的条件是调整节点的左右子树都为大堆或者小堆
//思路为从下标为parent位置开始向下的孩子节点不断比较进行调整,直到最后一个数据,
//所以需要传参堆的有效数据个数n
{int leftchild = parent * 2 + 1;//这里默认左孩子大于右孩子while (leftchild < n){int rightchild = parent * 2 + 2;if (rightchild < n && a[leftchild] < a[rightchild]){//rightchild < n是判断一下该父亲节点是否有右孩子,防止数组越界//默认左孩子大于右孩子//若右孩子大于左孩子则交换下标Swap(&leftchild, &rightchild);}if (a[parent] < a[leftchild]){Swap(&a[parent], &a[leftchild]);//若不符合堆的要求则交换parent = leftchild;//将原父亲数据对应下标也赋值过来leftchild = parent * 2 + 1;//新的孩子的下标}else//若符合堆的要求就退出循环{break;}}}
返回堆的个数
堆的个数就用int类型就好了,所以返回类型为int
int HeapSize(HP* php)//返回堆的个数
{assert(php);return php->size;
}
返回堆顶数据
因为返回值是堆顶数据,所以返回类型为堆的数据类型
HPDateType HeapTop(HP* php)//返回堆顶数据
{assert(php);return php->a[0];
}
判断堆是否为空
返回值为布尔类型——bool,当堆的有效数据size为0,则证明堆为空
bool HeapEmpty(HP* php)//判断是否为空,空返回ture 非空返回false
{assert(php);return php->size == 0;
}