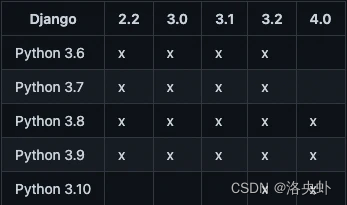
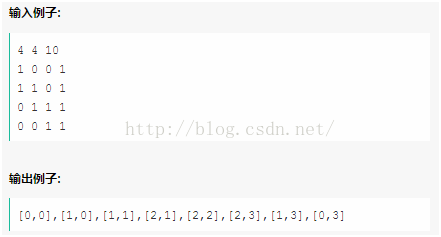
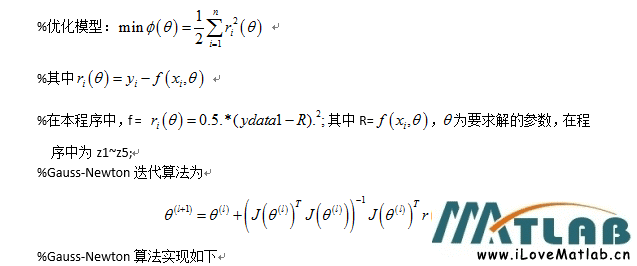D. Deleting Divisors

传送门：CF

题目如下：

前言：

显而易见，这题是一道博弈题。

初解此题大致思路和标答一致，但还是没有想的很清楚，所以还是没有过。

思路：

在做博弈题的时候，一定要想清楚必胜条件。

这题的必胜条件很明显，即，保证敌对方拿到一个质数。我们又知道质数一定是奇数（2除外）。

所以每个人的当前决策都要将局面转向对自己有利的方向，也就是要尽可能的让对手处于奇数状态。

再看题目，题目要求每次减一个divisor，那么构成奇数就有两种情况：第一种是我拿到了偶数，减一个奇数的除数；第二种是我拿到的是奇数，减一个偶数除数。

我们先分析第二种情况：先问自己一个问题，奇数的构成情况是怎么样的？一个奇数有可能存在偶数的除数吗？这个显然不存在。

所以如果Alice先手拿到的是奇数，那么她第一步一定是减去一个奇数，使Bob拿到的是一个偶数，所以现在问题的关键在于分析出偶数的情况。

下面分析第一种情况：当Alice先手拿到的是偶数，那么偶数分两种，第一种是这个偶数是由偶数*偶数构成的，第二种是由奇数*偶数构成的。

如果是奇数*偶数构成的，Alice先手一定是减一个奇数，使用得Bob拿到的数是一个奇数，而Bob只能选择减一个奇数，所以Alice拿到的还是一个偶数，如此反复，可以得到Bob无论什么时候都是奇数，Alice什么时候都是偶数，所以当先手拿到的是一个奇数*偶数的偶数时，必胜。

如果是由偶数*偶数 构成的，那么这个偶数就可以表示为 $2^{n}$ ，于是Alice先手可以减的数的范围是 $2\rightarrow 2^{n-1}$ ，如果Alice选择的是比 $2^{n-1}$ 小的数，那么Bob后手拿到的一定是一个奇数*偶数的数，由上面分析知道，此时先手必赢，即Bob赢。那么Alice一定不会选择比 $2^{n-1}$ 还小的数，她一定会选择减 $2^{n-1}$ ，如此反复，Bob也不傻，他也会选择减 $2^{n-1}$ ，那么可以分析得出，如果n是奇数，最后Alice会拿到2（Bob赢），如果n是偶数，Bob最后会拿到2（Alice赢）。

再回头看Alice先手拿到的是奇数的情况，因为Alice只能减奇数，所以Bob拿到的一定是一个奇数*偶数的偶数，由之前的分析知Bob必赢，也就是先手拿奇数必输。

综上：

先手拿奇数，后手必赢。

先手拿奇数*偶数的偶数，先手必赢。

先手拿偶数*偶数的偶数（ $2^{n}$ ），如果n是奇数后手必赢，反则先手必赢。

AC代码如下：

#include<bits/stdc++.h>
using namespace std;
int main()
{ios::sync_with_stdio(false);cin.tie(0);int T;cin >> T;while (T--){int n;cin >> n;if (n % 2 == 1)cout << "Bob" << endl;else{int num = 0;while (n % 2 == 0){n /= 2;num++;}if (n != 1)cout << "Alice" << endl;else{if (num % 2 == 1)cout << "Bob" << endl;else cout << "Alice" << endl;}}}return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://xiahunao.cn/news/1381829.html

如若内容造成侵权/违法违规/事实不符，请联系瞎胡闹网进行投诉反馈，一经查实，立即删除！