1. Z3安装

linux安装Z3

git clone https://github.com/angr/angr-z3.git
cd angr-z3
python scripts/mk_make.py
cd build
make
sudo make install

其中第三个命令有参数，自定义z3包的安装位置

python scripts/mk_make.py --prefix=/home/palmer --python --pypkgdir=/home/palmer/.local/lib/python2.7/site-packagespython scripts/mk_make.py --prefix=想安装到的目录 --python --pypkgdir=你的python第三方库地址
prefix 我设置的用户根目录
pypkgdir 去找python的包目录

在这里插入图片描述

2. Z3语句

2.1. Z3语句基础

Op	Mnmonics	Description
0	true	恒真
1	flase	恒假
2	=	相等
3	distinct	不同
4	ite	if-then-else
5	and	n元合取（其中条件必须全部满足）
6	or	n元析取（其中条件满足之一即可）
7	iff	implication
8	xor	异或
9	not	否定
10	implies	Bi-implications

2.2. Z3语句讲解

2.2.1. Z3简单使用例子

from z3 import *
x = Int('x')  #声明未知数，类型是整数类型Int
y = Int('y')
solve(x > 2, y < 10, x + 2*y == 7)
#  输出   [y = 0, x = 7]

先定义了两个未知数x和y，类型是Z3内置的整数类型Int
solve() 函数会创造一个 solver，然后对括号中的约束条件进行求解，在 Z3 默认情况下只会找到满足条件的一组解。

2.2.2. 声明未知数

声明整数x = Int('x')
声明实数x = Real('x')
声明布尔类型x = Bool('x')
批量声明未知数加s
例：

a, b, c = Reals('a b c')  #声明3个实数
x, y, z = Ints('x y z')   #声明3个整数

更改类型

IntVal() 返回Z3整数
RealVal() 返回Z3实数
RatVal() 返回Z3有理数值

2.2.3. simplify()函数—对表达式进行化简

>>> simplify(x + y + 2*x + 3)
3 + 3*x + y >>>> simplify(x < y + x + 2)
Not(y <= -2) >>>> simplify(And(x + 1 >= 3, x**2 + x**2 + y**2 + 2 >= 5))
And(x >= 2, 2*x**2 + y**2 >= 3) >>>> simplify((x + 1)*(y + 1))
(1 + x)*(1 + y) >>>> simplify((x + 1)*(y + 1), som=True) # sum-of-monomials： 单项式的和
1 + x + y + x*y>>>> t = simplify((x + y)**3, som=True) 
>>>> t
x*x*x + 3*x*x*y + 3*x*y*y + y*y*y>>>> simplify(t, mul_to_power=True) # mul_to_power 将乘法 转换成乘方
x**3 + 2*y*x**2 + x**2*y + 3*x*y**2 + y**3

simplify(<表达式>)  #对表达式进行化简
simplify(<表达式>,som=True)   #sum-of-monomials： 单项式的和    将表达式转成单项式的和
simplify(<表达式>,mul_to_power=True)   # mul_to_power  将乘法转换为乘方

simplify() 函数用于对表达式进行化简，同时可以设置一些选项来满足不同的要求。
更多选项使用 help_simplify() 获得。

2.2.4. set_param()函数配置全局变量

>>> x = Real('x')
>>> y = Real('y')
>>> solve(x**2 + y**2 == 3, x**3 == 2)
[x = 1.2599210498?, y = -1.1885280594?]>>> set_param(precision=30)
>>> solve(x**2 + y**2 == 3, x**3 == 2)
[x = 1.259921049894873164767210607278?, y = -1.188528059421316533710369365015?]

set_param(precision=30)  #保留30位的小数

set_param(rational_to_decimal=True) # 以十进制形式表示有理数

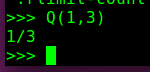
2.2.5. Q(a, b) 返回有理数 a/b

Q(a, b) 返回有理数 a/b
在这里插入图片描述

2.2.6. solver类系列

>>> from z3 import *
>>> x = Int('x')
>>> y = Int('y')
>>> s = Solver()
#创造一个通用solver
>>> type(s)
# Solver 类
<class ' Z3. z3. Solver'>>>> s.add(x>10,y==x+2)  #添加约束到solver 中
>>> s
[x>10,y==x+2]
>>> s.check()   #检查solver中的约束 是否满足
sat   # satisfiable/满足>>> s. push( )   #创建一个回溯点，即将当前栈的大小保存下来>>> s.add(y < 11)
>>> s
[x>10,y==x+2，y<11]
>>> s.check()
unsat   # unsatisfiable/不满足
>>> s. pop(num=1)   #回溯num个点
>>> s
[x>10，y==X+2]
>>> s. check()
sat
>>> for C in s.assertions():
# assertions() 返回一个包含所有约束的AstVector>>> s. statistics( )
# statistics() 返回最后一个check() 的统计信息
(   :max- memory	 6.26:memory  		 4.37:mk -bool -var	 1:num- al locs	331960806:rlimit-count 7016)
>>> m = s.model( )   # model() 返回最后一个check() 的model
>>> type(m)   # ModelRef 类
<class ' Z3. z3. ModelRef '>
>>> m
[x=11,y=13]
>>> for d in m.dec1s():   # decls()返回model包含了所有符号的列表
print("%S = %S" % (d.name()，m[d]))
x=11
y =13

3. Z3约束器使用流程

创建变量
例：

x = Int('x') 
y = Int('y')

创建solver求解器
例：s = Solver()
添加约束条件
例：s.add(x+y==10)
检查solver中的约束是否满足
例：s.check()
利用model()输出运算结果
例：s.model()

Z3-example

from z3 import *
v2=[18564, 37316, 32053, 33278, 23993, 33151,15248, 13719, 34137, 27391, 28639, 18453, 28465,12384, 20780, 45085, 35827, 37243, 26037, 39409,17583, 20825, 44474, 35138, 36914, 25918, 38915,17672, 21219, 43935, 37072, 39359, 27793, 41447,18098, 21335, 46164, 38698, 39084, 29205, 40913,19117, 21786, 46573, 38322, 41017, 29298, 43409,19655]
s = Solver()#设置一个解方程的类Solver(必须要设置）
a1 = [0]*49 #设置的列表长度为49，从0到48，因为下面这个如果是空列表的话不能用索引
for i in range(49):a1[i] = Int('a1['+str(i)+']')
#这里的3行  是设置未知量，都要设置，Int是设置int型的
s.add(v2[0] == 34 * a1[3] + 12 * a1[0] + 53 * a1[1] + 6 * a1[2] + 58 * a1[4] + 36 * a1[5] + a1[6])
s.add(v2[1] == 27 * a1[4] + 73 * a1[3] + 12 * a1[2] + 83 * a1[0] + 85 * a1[1] + 96 * a1[5] + 52 * a1[6])
s.add(v2[2] == 24 * a1[2] + 78 * a1[0] + 53 * a1[1] + 36 * a1[3] + 86 * a1[4] + 25 * a1[5] + 46 * a1[6])
s.add(v2[3] == 78 * a1[1] + 39 * a1[0] + 52 * a1[2] + 9 * a1[3] + 62 * a1[4] + 37 * a1[5] + 84 * a1[6])
s.add(v2[4] == 48 * a1[4] + 6 * a1[1] + 23 * a1[0] + 14 * a1[2] + 74 * a1[3] + 12 * a1[5] + 83 * a1[6])
s.add(v2[5] == 15 * a1[5] + 48 * a1[4] + 92 * a1[2] + 85 * a1[1] + 27 * a1[0] + 42 * a1[3] + 72 * a1[6])
s.add(v2[6] == 26 * a1[5] + 67 * a1[3] + 6 * a1[1] + 4 * a1[0] + 3 * a1[2] + 68 * a1[6])
s.add(v2[7] == 34 * a1[10] + 12 * a1[7] + 53 * a1[8] + 6 * a1[9] + 58 * a1[11] + 36 * a1[12] + a1[13])
s.add(v2[8] == 27 * a1[11] + 73 * a1[10] + 12 * a1[9] + 83 * a1[7] + 85 * a1[8] + 96 * a1[12] + 52 * a1[13])
s.add(v2[9] == 24 * a1[9] + 78 * a1[7] + 53 * a1[8] + 36 * a1[10] + 86 * a1[11] + 25 * a1[12] + 46 * a1[13])
s.add(v2[10] == 78 * a1[8] + 39 * a1[7] + 52 * a1[9] + 9 * a1[10] + 62 * a1[11] + 37 * a1[12] + 84 * a1[13])
s.add(v2[11] == 48 * a1[11] + 6 * a1[8] + 23 * a1[7] + 14 * a1[9] + 74 * a1[10] + 12 * a1[12] + 83 * a1[13])
s.add(v2[12] == 15 * a1[12] + 48 * a1[11] + 92 * a1[9] + 85 * a1[8] + 27 * a1[7] + 42 * a1[10] + 72 * a1[13])
s.add(v2[13] == 26 * a1[12] + 67 * a1[10] + 6 * a1[8] + 4 * a1[7] + 3 * a1[9] + 68 * a1[13])
s.add(v2[14] == 34 * a1[17] + 12 * a1[14] + 53 * a1[15] + 6 * a1[16] + 58 * a1[18] + 36 * a1[19] + a1[20])
s.add(v2[15] == 27 * a1[18] + 73 * a1[17] + 12 * a1[16] + 83 * a1[14] + 85 * a1[15] + 96 * a1[19] + 52 * a1[20])
s.add(v2[16] == 24 * a1[16] + 78 * a1[14] + 53 * a1[15] + 36 * a1[17] + 86 * a1[18] + 25 * a1[19] + 46 * a1[20])
s.add(v2[17] == 78 * a1[15] + 39 * a1[14] + 52 * a1[16] + 9 * a1[17] + 62 * a1[18] + 37 * a1[19] + 84 * a1[20])
s.add(v2[18] == 48 * a1[18] + 6 * a1[15] + 23 * a1[14] + 14 * a1[16] + 74 * a1[17] + 12 * a1[19] + 83 * a1[20])
s.add(v2[19] == 15 * a1[19] + 48 * a1[18] + 92 * a1[16] + 85 * a1[15] + 27 * a1[14] + 42 * a1[17] + 72 * a1[20])
s.add(v2[20] == 26 * a1[19] + 67 * a1[17] + 6 * a1[15] + 4 * a1[14] + 3 * a1[16] + 68 * a1[20])
s.add(v2[21] == 34 * a1[24] + 12 * a1[21] + 53 * a1[22] + 6 * a1[23] + 58 * a1[25] + 36 * a1[26] + a1[27])
s.add(v2[22] == 27 * a1[25] + 73 * a1[24] + 12 * a1[23] + 83 * a1[21] + 85 * a1[22] + 96 * a1[26] + 52 * a1[27])
s.add(v2[23] == 24 * a1[23] + 78 * a1[21] + 53 * a1[22] + 36 * a1[24] + 86 * a1[25] + 25 * a1[26] + 46 * a1[27])
s.add(v2[24] == 78 * a1[22] + 39 * a1[21] + 52 * a1[23] + 9 * a1[24] + 62 * a1[25] + 37 * a1[26] + 84 * a1[27])
s.add(v2[25] == 48 * a1[25] + 6 * a1[22] + 23 * a1[21] + 14 * a1[23] + 74 * a1[24] + 12 * a1[26] + 83 * a1[27])
s.add(v2[26] == 15 * a1[26] + 48 * a1[25] + 92 * a1[23] + 85 * a1[22] + 27 * a1[21] + 42 * a1[24] + 72 * a1[27])
s.add(v2[27] == 26 * a1[26] + 67 * a1[24] + 6 * a1[22] + 4 * a1[21] + 3 * a1[23] + 68 * a1[27])
s.add(v2[28] == 34 * a1[31] + 12 * a1[28] + 53 * a1[29] + 6 * a1[30] + 58 * a1[32] + 36 * a1[33] + a1[34])
s.add(v2[29] == 27 * a1[32] + 73 * a1[31] + 12 * a1[30] + 83 * a1[28] + 85 * a1[29] + 96 * a1[33] + 52 * a1[34])
s.add(v2[30] == 24 * a1[30] + 78 * a1[28] + 53 * a1[29] + 36 * a1[31] + 86 * a1[32] + 25 * a1[33] + 46 * a1[34])
s.add(v2[31] == 78 * a1[29] + 39 * a1[28] + 52 * a1[30] + 9 * a1[31] + 62 * a1[32] + 37 * a1[33] + 84 * a1[34])
s.add(v2[32] == 48 * a1[32] + 6 * a1[29] + 23 * a1[28] + 14 * a1[30] + 74 * a1[31] + 12 * a1[33] + 83 * a1[34])
s.add(v2[33] == 15 * a1[33] + 48 * a1[32] + 92 * a1[30] + 85 * a1[29] + 27 * a1[28] + 42 * a1[31] + 72 * a1[34])
s.add(v2[34] == 26 * a1[33] + 67 * a1[31] + 6 * a1[29] + 4 * a1[28] + 3 * a1[30] + 68 * a1[34])
s.add(v2[35] == 34 * a1[38] + 12 * a1[35] + 53 * a1[36] + 6 * a1[37] + 58 * a1[39] + 36 * a1[40] + a1[41])
s.add(v2[36] == 27 * a1[39] + 73 * a1[38] + 12 * a1[37] + 83 * a1[35] + 85 * a1[36] + 96 * a1[40] + 52 * a1[41])
s.add(v2[37] == 24 * a1[37] + 78 * a1[35] + 53 * a1[36] + 36 * a1[38] + 86 * a1[39] + 25 * a1[40] + 46 * a1[41])
s.add(v2[38] == 78 * a1[36] + 39 * a1[35] + 52 * a1[37] + 9 * a1[38] + 62 * a1[39] + 37 * a1[40] + 84 * a1[41])
s.add(v2[39] == 48 * a1[39] + 6 * a1[36] + 23 * a1[35] + 14 * a1[37] + 74 * a1[38] + 12 * a1[40] + 83 * a1[41])
s.add(v2[40] == 15 * a1[40] + 48 * a1[39] + 92 * a1[37] + 85 * a1[36] + 27 * a1[35] + 42 * a1[38] + 72 * a1[41])
s.add(v2[41] == 26 * a1[40] + 67 * a1[38] + 6 * a1[36] + 4 * a1[35] + 3 * a1[37] + 68 * a1[41])
s.add(v2[42] == 34 * a1[45] + 12 * a1[42] + 53 * a1[43] + 6 * a1[44] + 58 * a1[46] + 36 * a1[47] + a1[48])
s.add(v2[43] == 27 * a1[46] + 73 * a1[45] + 12 * a1[44] + 83 * a1[42] + 85 * a1[43] + 96 * a1[47] + 52 * a1[48])
s.add(v2[44] == 24 * a1[44] + 78 * a1[42] + 53 * a1[43] + 36 * a1[45] + 86 * a1[46] + 25 * a1[47] + 46 * a1[48])
s.add(v2[45] == 78 * a1[43] + 39 * a1[42] + 52 * a1[44] + 9 * a1[45] + 62 * a1[46] + 37 * a1[47] + 84 * a1[48])
s.add(v2[46] == 48 * a1[46] + 6 * a1[43] + 23 * a1[42] + 14 * a1[44] + 74 * a1[45] + 12 * a1[47] + 83 * a1[48])
s.add(v2[47] == 15 * a1[47] + 48 * a1[46] + 92 * a1[44] + 85 * a1[43] + 27 * a1[42] + 42 * a1[45] + 72 * a1[48])
s.add(v2[48] == 26 * a1[47] + 67 * a1[45] + 6 * a1[43] + 4 * a1[42] + 3 * a1[44] + 68 * a1[48])
#add是添加约束条件
print(s.check())#check是保证有解
answer=s.model()#model是输出运算结果
print(answer)